Soalan 6:
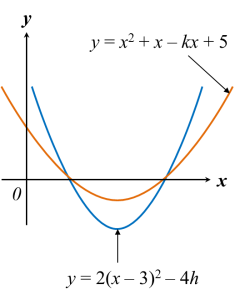
Rajah di atas menunjukkan graf lengkung y = x2 + x – kx + 5 dan y = 2(x – 3) – 4h yang bersilang pada dua titik pada paksi-x. Cari
(a) nilai k dan nilai h,
(b) nilai minimum bagi kedua-dua lengkung itu.
Penyelesaian:
(a)
y=x2+x−kx+5=x2+(1−k)x+5=[x+(1−k)2]2−(1−k2)2+5paksi simetri bagi graf ini ialahx=−(1−k)2
y=2(x−3)2−4hpaksi simetri bagi graf ini ialahx=3.Maka, −1−k2=3 −1+k=6 k=7
Gantikan k=7 ke dalam persamaany=x2+x−7x+5 =x2−6x+5Pada paksi−x,y=0;x2−6x+5=0(x−1)(x−5)=0x=1,5
Pada titik (1,0)Gantikan x=1,y=0 ke dalam graf:y=2(x−3)2−4h0=2(1−3)2−4h4h=2(4)4h=8h=2
(b)
Lengkung y=x2−6x+5=(x−3)2−9+5=(x−3)2−4Maka, nilai minimumnya=−4.Bagi lengkung y=2(x−3)2−8, nilai minimum=−8.

Rajah di atas menunjukkan graf lengkung y = x2 + x – kx + 5 dan y = 2(x – 3) – 4h yang bersilang pada dua titik pada paksi-x. Cari
(a) nilai k dan nilai h,
(b) nilai minimum bagi kedua-dua lengkung itu.
Penyelesaian:
(a)
y=x2+x−kx+5=x2+(1−k)x+5=[x+(1−k)2]2−(1−k2)2+5paksi simetri bagi graf ini ialahx=−(1−k)2
y=2(x−3)2−4hpaksi simetri bagi graf ini ialahx=3.Maka, −1−k2=3 −1+k=6 k=7
Gantikan k=7 ke dalam persamaany=x2+x−7x+5 =x2−6x+5Pada paksi−x,y=0;x2−6x+5=0(x−1)(x−5)=0x=1,5
Pada titik (1,0)Gantikan x=1,y=0 ke dalam graf:y=2(x−3)2−4h0=2(1−3)2−4h4h=2(4)4h=8h=2
(b)
Lengkung y=x2−6x+5=(x−3)2−9+5=(x−3)2−4Maka, nilai minimumnya=−4.Bagi lengkung y=2(x−3)2−8, nilai minimum=−8.