Soalan 9 (10 markah):
Rajah 5 menunjukkan segi tiga ABC. Garis lurus AE bersilang dengan garis lurus BC di titik D. Titik V terletak pada garis lurus AE.
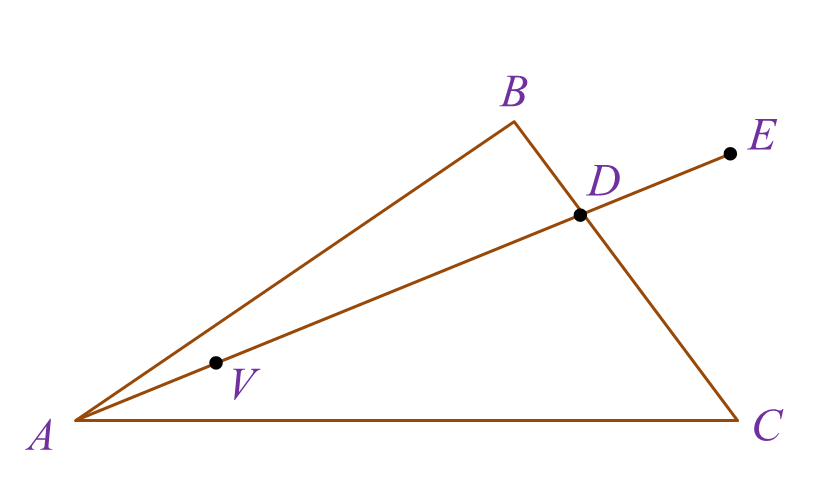
Diberi bahawa →BD=13→BC,→AC=6x˜ dan →AB=9y˜.(a) Ungkapkan dalam sebutan x˜ dan / atau y˜: (i) →BC, (ii) →AD.(b) Diberi bahawa →AV=m→AD dan →BV=n(x˜−9y˜), dengan keadaan m dan n ialah pemalar. Cari nilai m dan nilai n.(c) Diberi →AE=hx˜+9y˜, dengan keadaan h ialah pemalar, cari nilai h.
Penyelesaian:
(a)(i)
→BC=→BA+→AC =−9y˜+6x˜ =6x˜−9y˜
(a)(ii)
→AD=→AB+→BD =9y˜+13→BC =9y˜+13(6x˜−9y˜) =9y˜+2x˜−3y˜ =2x˜+6y˜
(b)
Diberi →AV=m→AD=m(2x˜+6y˜)=2mx˜+6my˜→AV=→AB+→BV = 9y˜+n(x˜−9y˜) =9y˜+nx˜−9ny˜ =nx˜+(9−9n)y˜Dengan menyamakan pekali bagi x˜ dan y˜, 2mx˜+6my˜=nx˜+(9−9n)y˜2m=nn=2m.............(1)6m=9−9n.............(2)Gantikan (1) ke dalam (2),6m=9−9(2m)6m=9−18m24m=9m=924=38Daripada (1):n=2(38)=34
(c)
A, D dan E adalah segaris.→AD=k(→AE)→AD=k(hx˜+9y˜)2x˜+6y˜=khx˜+9ky˜Dengan menyamakan pekali bagi y˜:9k=6k=69k=23Dengan menyamakan pekali bagi x˜:kh=2(23)h=2h=2×32h=3
Rajah 5 menunjukkan segi tiga ABC. Garis lurus AE bersilang dengan garis lurus BC di titik D. Titik V terletak pada garis lurus AE.

Diberi bahawa →BD=13→BC,→AC=6x˜ dan →AB=9y˜.(a) Ungkapkan dalam sebutan x˜ dan / atau y˜: (i) →BC, (ii) →AD.(b) Diberi bahawa →AV=m→AD dan →BV=n(x˜−9y˜), dengan keadaan m dan n ialah pemalar. Cari nilai m dan nilai n.(c) Diberi →AE=hx˜+9y˜, dengan keadaan h ialah pemalar, cari nilai h.
Penyelesaian:
(a)(i)
→BC=→BA+→AC =−9y˜+6x˜ =6x˜−9y˜
(a)(ii)
→AD=→AB+→BD =9y˜+13→BC =9y˜+13(6x˜−9y˜) =9y˜+2x˜−3y˜ =2x˜+6y˜
(b)
Diberi →AV=m→AD=m(2x˜+6y˜)=2mx˜+6my˜→AV=→AB+→BV = 9y˜+n(x˜−9y˜) =9y˜+nx˜−9ny˜ =nx˜+(9−9n)y˜Dengan menyamakan pekali bagi x˜ dan y˜, 2mx˜+6my˜=nx˜+(9−9n)y˜2m=nn=2m.............(1)6m=9−9n.............(2)Gantikan (1) ke dalam (2),6m=9−9(2m)6m=9−18m24m=9m=924=38Daripada (1):n=2(38)=34
(c)
A, D dan E adalah segaris.→AD=k(→AE)→AD=k(hx˜+9y˜)2x˜+6y˜=khx˜+9ky˜Dengan menyamakan pekali bagi y˜:9k=6k=69k=23Dengan menyamakan pekali bagi x˜:kh=2(23)h=2h=2×32h=3