Soalan 3 (10 markah):
(a) Buktikan sin(3x+π6)−sin(3x−π6)=kos3x(b) Seterusnya,(i) selesaikan persamaan sin(3x2+π6)−sin(3x2−π6)=12 untuk 0≤x≤2π dan beri jawapan anda dalam bentuk pencahan termudah dalam sebutan π radian,(ii) lakar graf bagi y=sin(3x+π6)−sin(3x−π6)−12 untuk 0≤x≤π.
Penyelesaian:
(a) Sebelah kiri,sin(3x+π6)−sin(3x−π6)=[sin3xkosπ6+kos3xsinπ6]−[sin3xkosπ6−kos3xsinπ6]=2[kos3xsinπ6]=2[kos3x(12)]=kos3x(sebelah kanan)
(b)(i)sin(3x2+π6)−sin(3x2−π6)=12,0≤x≤2πkos3x2=123x2=π3,(2π−π3),(2π+π3)3x2=π3,5π3,7π3x=2π9,10π9,14π9
(b)(ii) y=sin(3x+π6)−sin(3x−π6)−12 untuk 0≤x≤π.y=kos3x−12
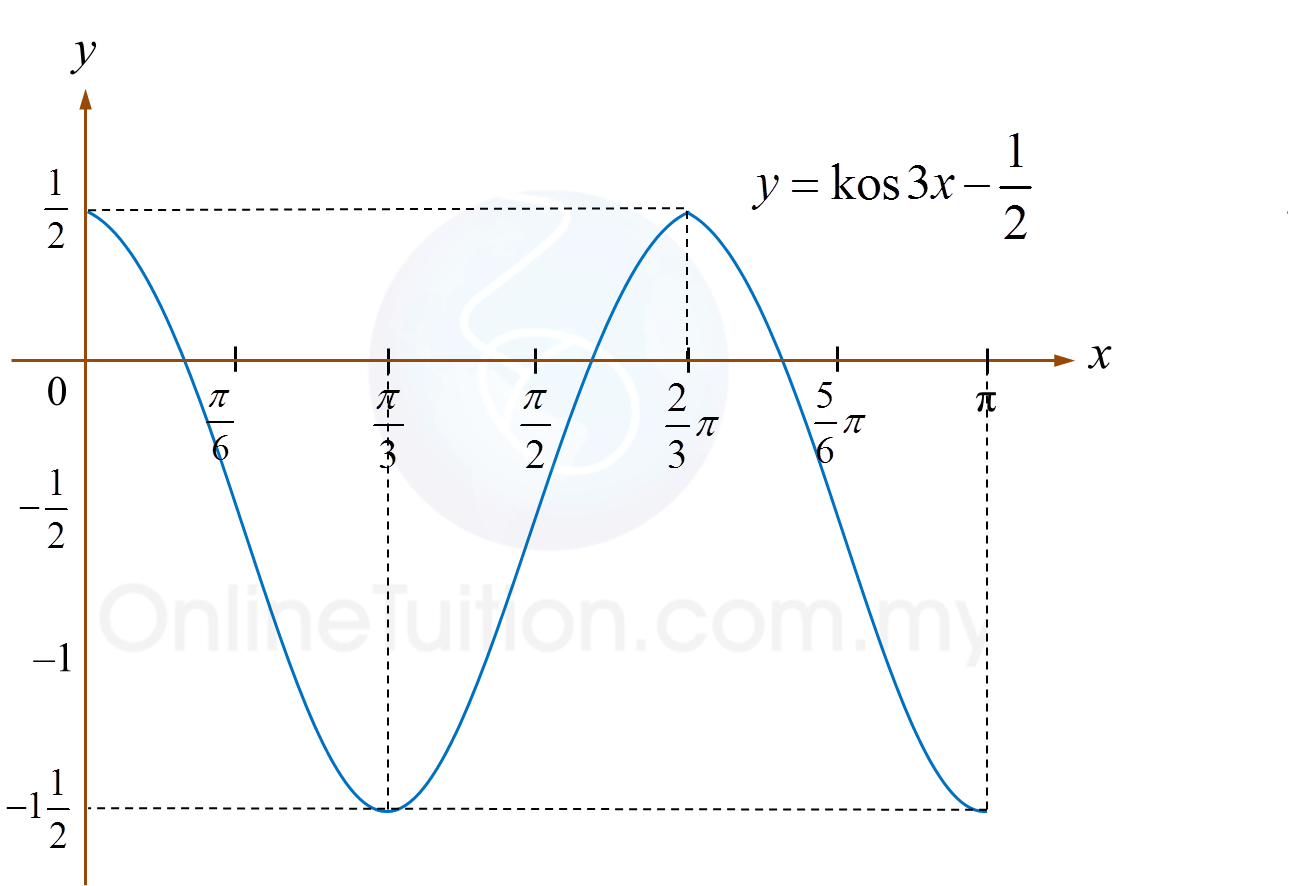
(a) Buktikan sin(3x+π6)−sin(3x−π6)=kos3x(b) Seterusnya,(i) selesaikan persamaan sin(3x2+π6)−sin(3x2−π6)=12 untuk 0≤x≤2π dan beri jawapan anda dalam bentuk pencahan termudah dalam sebutan π radian,(ii) lakar graf bagi y=sin(3x+π6)−sin(3x−π6)−12 untuk 0≤x≤π.
Penyelesaian:
(a) Sebelah kiri,sin(3x+π6)−sin(3x−π6)=[sin3xkosπ6+kos3xsinπ6]−[sin3xkosπ6−kos3xsinπ6]=2[kos3xsinπ6]=2[kos3x(12)]=kos3x(sebelah kanan)
(b)(i)sin(3x2+π6)−sin(3x2−π6)=12,0≤x≤2πkos3x2=123x2=π3,(2π−π3),(2π+π3)3x2=π3,5π3,7π3x=2π9,10π9,14π9
(b)(ii) y=sin(3x+π6)−sin(3x−π6)−12 untuk 0≤x≤π.y=kos3x−12
