Soalan 5:
(a) Buktikan
2tanx2−sek2x=tan2x.
(b) (i) Lakar graf y = – tan 2x untuk 0 ≤ x ≤ π.
(b) (ii) Seterusnya, dengan menggunakan paksi yang sama, lakar satu garis lurus yang sesuai untuk
mencari bilangan penyelesaian bagi persamaan 3xπ+2tanx2−sek2x=0 untuk 0 ≤ x ≤ π.
Nyatakan bilangan penyelesaian itu.
(b) (ii) Seterusnya, dengan menggunakan paksi yang sama, lakar satu garis lurus yang sesuai untuk
mencari bilangan penyelesaian bagi persamaan 3xπ+2tanx2−sek2x=0 untuk 0 ≤ x ≤ π.
Nyatakan bilangan penyelesaian itu.
Penyelesaian:
(a)
2tanx2−sek2x=tan2xSebelah kiri:2tanx2−sek2x=2tanx2−(1+tan2x)=2tanx2−tan2x=tan2x(Sebelah kanan)
(b)(i)
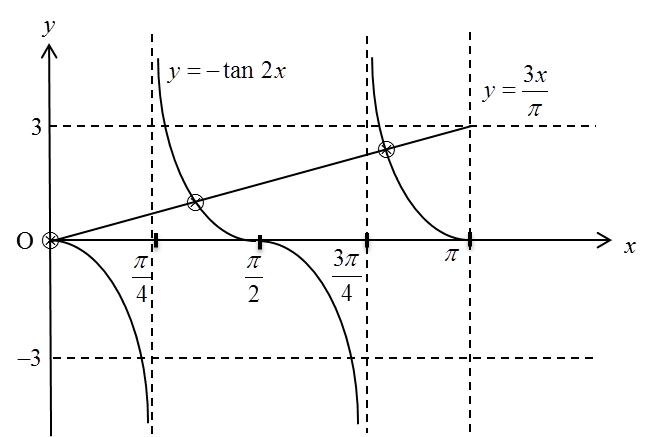
(b)(ii)
3xπ+2tanx2−sek2x=03xπ+tan2x=0←dari (a)−tan2x=3xπ y=3xπGraf yang sesuai dilakar ialah y=3xπ.
Apabila x = 0, y = 0
Apabila x = π, y = 3
Bilangan penyelesaian = 3