8.4.3 Taburan Kebarangkalian, SPM Praktis (Kertas 2)

Soalan 6:
Dalam suatu kajian di sebuah daerah tertentu, didapati tiga daripada lima keluarga memiliki televisyen LCD.
Jika 10 keluarga dari daerah itu dipilih secara rawak, hitung kebarangkalian bahawa sekurang-kurangnya 8 keluarga memiliki sebuah televisyen LCD.

Penyelesaian:
$\begin{array}{l}\text{Katakan }X\text{ adalah pembolehubah rawak yang mewakili bilangan}\\ \text{keluarga yang memiliki televisyen LCD}\text{.}\\ X~B\left(n,p\right)\\ X~B\left(10,\frac{3}{5}\right)\\ p=\frac{3}{5}=0.6\\ q=1-0.6=0.4\\ \\ P(X=r)={}^{n}c{}_r.p^r.q^{n-r}\\ P\left(\text{sekurang-kurangnya 8 keluarga memiliki televisyen LCD}\right)\\ P(X\ge 8)\\ =P\left(X=8\right)+P\left(X=9\right)+P\left(X=10\right)\\ ={}^{10}C{}_8{\left(0.6\right)}^8{\left(0.4\right)}^2+{}^{10}C{}_9{\left(0.6\right)}^9{\left(0.4\right)}^1+{}^{10}C{}_{10}{\left(0.6\right)}^{10}{\left(0.4\right)}^0\\ =0.1209+0.0403+0.0060\\ =0.1672\end{array}$

Soalan 7:
Dalam sebuah sekolah berasrama penuh, 300 orang murid menduduki ujian kelayakan matematik. Markah yang diperoleh adalah mengikut taburan normal dengan min 56 dan sisihan piawai 8.
(a) Cari bilangan murid yang lulus ujian matematik itu jika markah lulus ialah 40.
(b) Jika 12% daripada murid itu lulus ujian tersebut dengan mendapat gred A, cari markah minimum untuk mendapat gred A.


Penyelesaian:
$\begin{array}{l}\text{Katakan }X=\text{markah yang diperoleh oleh murid-murid}\text{.}\\ X~N\left(56,8^2\right)\\ \left(a\right)P\left(X\ge 40\right)=P\left(Z\ge \frac{40-56}{8}\right)\\ =P\left(Z\ge -2\right)\\ =1-P\left(Z\ge 2\right)\\ =1-0.02275\\ =0.9773\\ \text{Bilangan murid yang lulus ujian matematik}\\ =0.9773\times 300\\ =293\\ \\ \left(b\right)\text{ Katakan markah minimum untuk mendapat gred }A\text{ ialah }k\\ P\left(X\ge k\right)=0.12\\ P\left(Z\ge \frac{k-56}{8}\right)=0.12\\ \frac{k-56}{8}=1.17\\ k=\left(1.17\right)\left(8\right)+56\\ =65.36\end{array}$

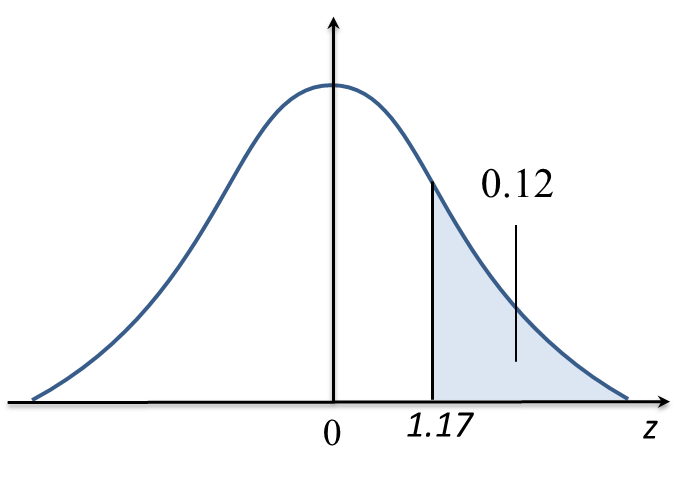Oleh itu, markah minimum untuk mendapat gred A ialah 66.