Soalan 5 (2 markah):
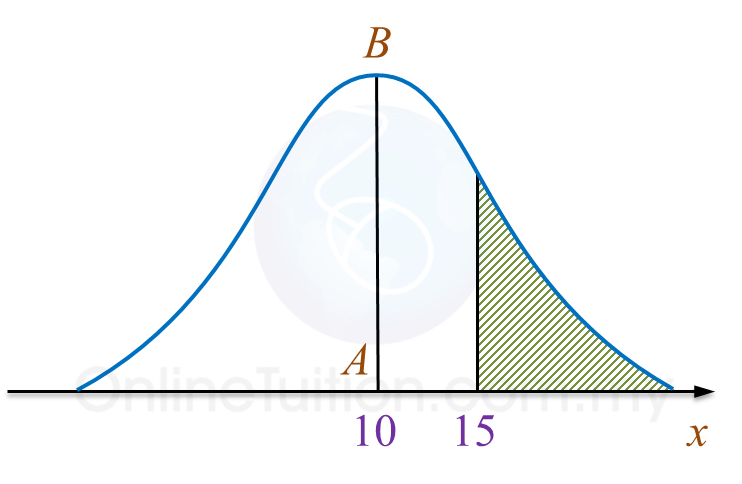
Rajah menunjukkan graf taburan kebarangkalian bagi suatu pemboleh ubah rawak X, X ~ N(μ, σ2).
 Rajah
Rajah
Diberi bahawa AB adalah paksi simetri bagi graf itu.
(a) Nyatakan nilai μ.
(b) Jika luas kawasan berlorek ialah 0.38, nyatakan nilai bagi P(5 ≤ X ≤ 15).
Penyelesaian:
(a)
μ = 0
(b)
P(10 ≤ X ≤ 15)
= 0.5 – 0.38
= 0.12
P(5 ≤ X ≤ 10)
= P(10 ≤ X ≤ 15)
= 0.12
Maka P(5 ≤ X ≤ 15)
= 0.12 + 0.12
= 0.24
Rajah menunjukkan graf taburan kebarangkalian bagi suatu pemboleh ubah rawak X, X ~ N(μ, σ2).
 Rajah
RajahDiberi bahawa AB adalah paksi simetri bagi graf itu.
(a) Nyatakan nilai μ.
(b) Jika luas kawasan berlorek ialah 0.38, nyatakan nilai bagi P(5 ≤ X ≤ 15).
Penyelesaian:
(a)
μ = 0
(b)
P(10 ≤ X ≤ 15)
= 0.5 – 0.38
= 0.12
P(5 ≤ X ≤ 10)
= P(10 ≤ X ≤ 15)
= 0.12
Maka P(5 ≤ X ≤ 15)
= 0.12 + 0.12
= 0.24
Soalan 6 (3 markah):
Rajah menunjukkan graf bagi taburan binomial X ~ B(3, p).
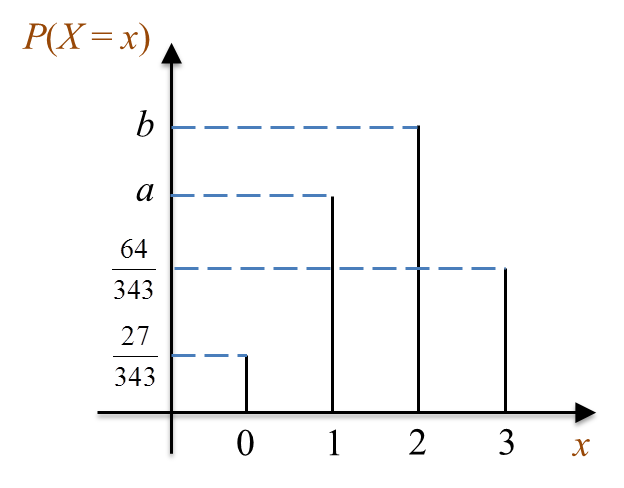 Rajah
Rajah
(a) Ungkapkan P(X = 0) + P(X > 2) dalam sebutan a dan b.
(b) Cari nilai p.
Penyelesaian:
(a)
P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 1
P(X = 0) + a + b + P(X = 3) = 1
P(X = 0) + P(X = 3) = 1 – a – b
P(X = 0) + P(X > 2) = 1 – a – b
(b)
P(X=0)=273433C0(p0)(1−p)3=273431×1×(1−p)3=(37)31−p=37p=47
Rajah menunjukkan graf bagi taburan binomial X ~ B(3, p).
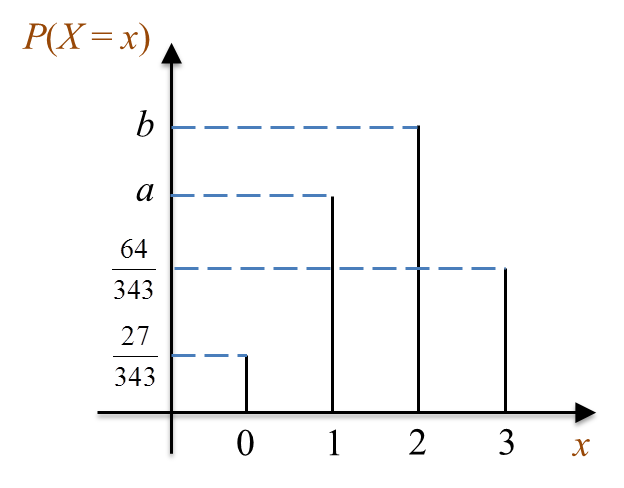 Rajah
Rajah (a) Ungkapkan P(X = 0) + P(X > 2) dalam sebutan a dan b.
(b) Cari nilai p.
Penyelesaian:
(a)
P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 1
P(X = 0) + a + b + P(X = 3) = 1
P(X = 0) + P(X = 3) = 1 – a – b
P(X = 0) + P(X > 2) = 1 – a – b
(b)
P(X=0)=273433C0(p0)(1−p)3=273431×1×(1−p)3=(37)31−p=37p=47