Bab 19 Taburan Kebarangkalian

Soalan 7 (4 markah):
Sebuah badan sukarela menganjurkan kursus pertolongan cemas 4 kali sebulan, setiap Sabtu dari Mac hingga September.
[Andaikan setiap bulan mempunyai empat hari Sabtu]

Salmah berhasrat untuk menyertai kursus tersebut tetapi dia mungkin perlu meluangkan satu hari Sabtu setiap bulan untuk menemani ibunya ke hospital.
Kebarangkalian bahawa Salmah akan hadir ke kursus tersebut pada setiap Sabtu ialah 0.8. Salmah akan diberi sijil kehadiran bulanan jika dia boleh menghadiri kursus tersebut sekurang-kurangnya 3 kali sebulan.

(a) Cari kebarangkalian bahawa Salmah akan diberi sijil kehadiran bulanan.

(b) Salmah akan layak untuk menduduki ujian pertolongan cemas jika dia memperoleh lebih daripada 5 sijil kehadiran bulanan.
Cari kebarangkalian bahawa Salmah layak untuk menduduki ujian pertolongan cemas itu.

Penyelesaian:
(a)

$\begin{array}{l}P\left(X=r\right)={}^{n}C{}_r{p}^r{q}^{n-r}\\ p=0.8,q=0.2,n=4,r=3,4\\ \\ P\left(X\ge 3\right)\\ =P\left(X=3\right)+P\left(X=4\right)\\ ={}^{4}C{}_3{\left(0.8\right)}^3{\left(0.2\right)}^1+{}^{4}C{}_4{\left(0.8\right)}^4{\left(0.2\right)}^0\\ =0.4096+0.4096\\ =0.8192\end{array}$

(b)

$\begin{array}{l}P\left(X=r\right)={}^{n}C{}_r{p}^r{q}^{n-r}\\ p=0.8192,q=0.1808,n=7,r=6,\text{ 7}\\ \\ P\left(X>5\right)\\ =P\left(X=6\right)+P\left(X=7\right)\\ ={}^{7}C{}_6{\left(0.8192\right)}^6{\left(0.1808\right)}^1+\\ {}^{7}C{}_7{\left(0.8192\right)}^7{\left(0.1808\right)}^0\\ =0.3825+0.2476\\ =0.6301\end{array}$

Soalan 8 (4 markah):
Rajah menunjukkan satu graf taburan normal piawai.

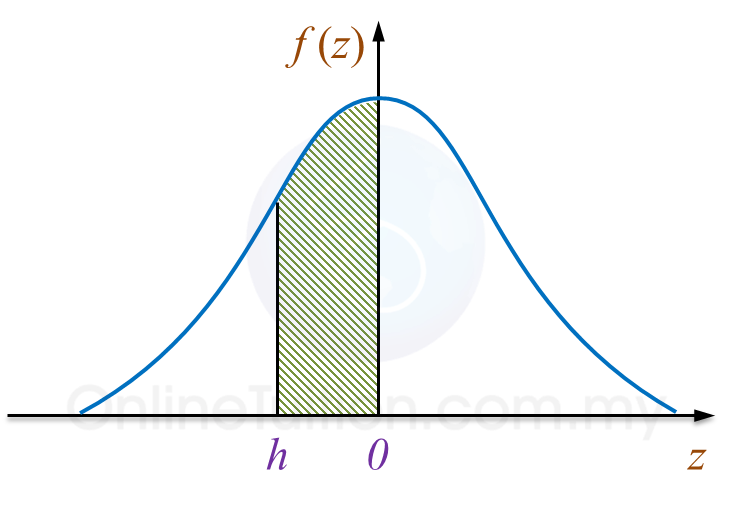Rajah

Kebarangkalian yang diwakili oleh luas kawasan berlorek ialah 0.2881.
(a) Cari nilai h.
(b) X ialah pemboleh ubah rawak selanjar bertaburan secara normal dengan min, μ dan varians 16.
Cari nilai μ jika skor-z bagi X = 58.8 ialah h.

Penyelesaian:
(a)
P(X < h) = 0.5 – 0.2881
P(X < h) = 0.2119
P(X < –0.8) = 0.2119
h = –0.8

(b)

$\begin{array}{l}X=58.8\\ \frac{X-\mu }{\sigma }=\frac{58.8-\mu }{\sigma }\\ Z=\frac{58.8-\mu }{4}\\ h=\frac{58.8-\mu }{4}\\ -0.8=\frac{58.8-\mu }{4}\\ -3.2=58.8-\mu \\ \mu =58.8+3.2\\ \mu =62\end{array}$