Question 4:
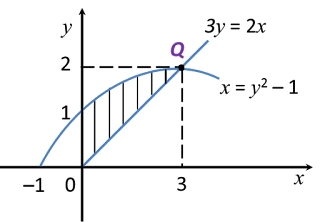
Diagram below shows a curve x = y2 – 1 which intersects the straight line 3y = 2x at point Q.
Calculate the volume generated when the shaded region is revolved 360o about the y-axis.
x=y2−1→(1)3y=2xx=32y→(2)Substitute (2) into (1),32y=y2−12y2−3y−2=0(2y+1)(y−2)=0y=−12 or y=2
When y=2,x=32(2)=3, Q=(3, 2)I1(Volume of cone)=13πr2h=13π(3)2(2)=6π unit3I2(Volume of the curve)= π∫21x2dy= π∫21(y2−1)2dy= π∫21(y4−2y2+1)dy=π[y55−2y33+y]21=π[(255−2(2)33+2)−(155−2(1)33+1)]=π(4615−815)=3815π unit3∴