Question 6:
Diagram below shows a trapezium OABC and point D lies on AC.
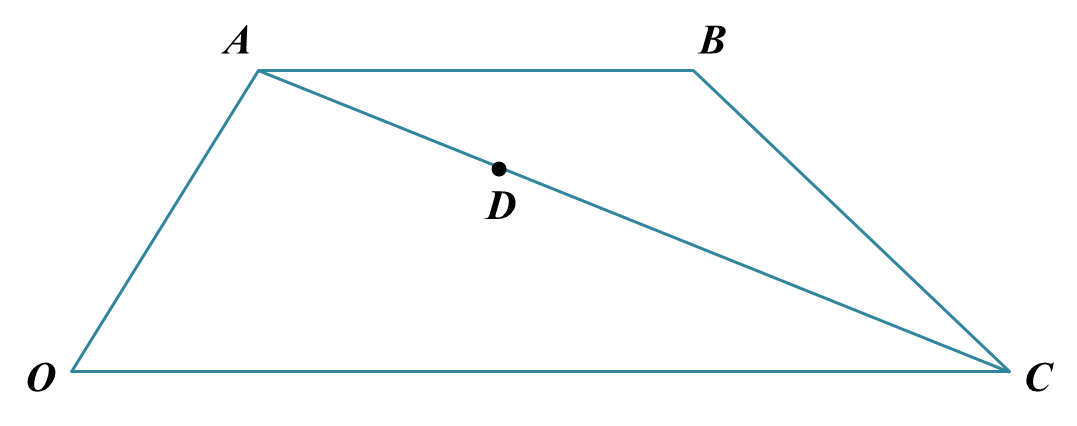
It is given that →OC=18b˜, →OA=6a˜ and →OC=2→AB.(a) Express in terms of a˜ and b˜,(i) →AC(ii) →OB(b) It is given that →AD=k→AC, where k is a constant.Find the value of k if the points O, D and B are collinear.
Solution:
(a)(i)
→AC=→AO+→OC =−6a˜+18b˜ =18b˜−6a˜
(a)(ii)
→OC=2→AB18b˜=2(→AO+→OB)18b˜=2(−6a˜+→OB)18b˜=−12a˜+2→OB→OB=6a˜+9b˜
(b)
→OD=h→OB=h(6a˜+9b˜)=6ha˜+9hb˜→AD=→OD−→OA=6ha˜+9hb˜−6a˜=a˜(6h−6)+9hb˜→AD=k→ACa˜(6h−6)+9hb˜=k(18b˜−6a˜)a˜(6h−6)+9hb˜=−6ka˜+18kb˜6h−6=−6kh−1=−kh=1−k..........(1)9h=18kh=2kFrom (1),1−k=2k3k=1k=13
Diagram below shows a trapezium OABC and point D lies on AC.

It is given that →OC=18b˜, →OA=6a˜ and →OC=2→AB.(a) Express in terms of a˜ and b˜,(i) →AC(ii) →OB(b) It is given that →AD=k→AC, where k is a constant.Find the value of k if the points O, D and B are collinear.
Solution:
(a)(i)
→AC=→AO+→OC =−6a˜+18b˜ =18b˜−6a˜
(a)(ii)
→OC=2→AB18b˜=2(→AO+→OB)18b˜=2(−6a˜+→OB)18b˜=−12a˜+2→OB→OB=6a˜+9b˜
(b)
→OD=h→OB=h(6a˜+9b˜)=6ha˜+9hb˜→AD=→OD−→OA=6ha˜+9hb˜−6a˜=a˜(6h−6)+9hb˜→AD=k→ACa˜(6h−6)+9hb˜=k(18b˜−6a˜)a˜(6h−6)+9hb˜=−6ka˜+18kb˜6h−6=−6kh−1=−kh=1−k..........(1)9h=18kh=2kFrom (1),1−k=2k3k=1k=13