Question 8:
Diagram below shows quadrilateral OPQR. The straight line PR intersects the straight line OQ at point S.
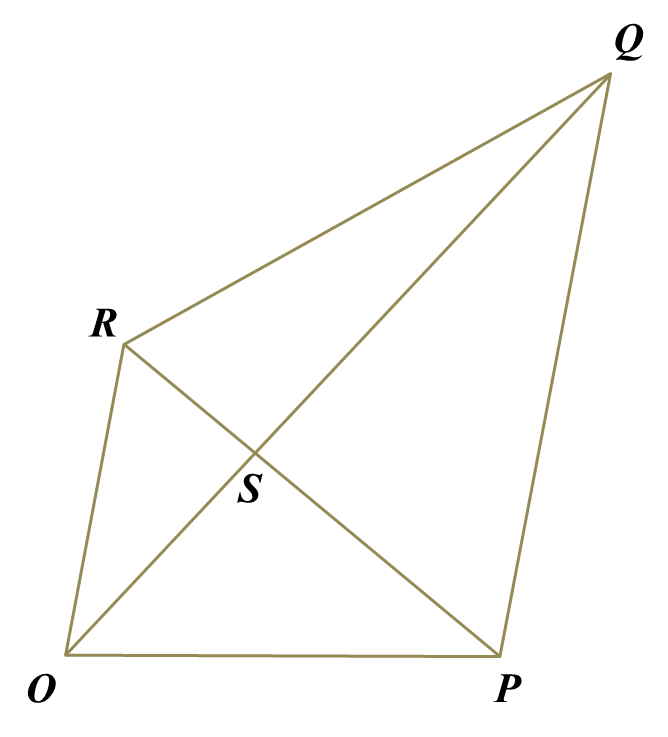
It is given that →OP=7x˜, →OR=5y˜, PS:SR=3:1 and →OR is parallel to →PQ.(a) Express in terms of x˜ and y˜,(i) →PR(ii) →OS(b) Using →PQ=m→OR and →SQ=n→OS, where m and n are constants, Find the value of m and of n.(c) Given that |y˜|=4 units and the area of ORS is 50 cm2, find the perpendicular distance from point S to OR.
Solution:
(a)(i)
→PR=→PO+→OR =−7x˜+5y˜
(a)(ii)
→OS=→OP+→PS =7x˜+34→PR =7x˜+34(−7x˜+5y˜) =7x˜−214x˜+154y˜ =74x˜+154y˜
(b)
→PS=→PQ−→SQ34→PR=m→OR−n→OS34(−7x˜+5y˜)=m(5y˜)−n(74x˜+154y˜)−214x˜+154y˜=5my˜−74nx˜−154my˜−214x˜+154y˜=−74nx˜+54my˜−21x˜+15y˜=−7nx˜+5my˜7n=21n=35m=15m=3
(c)
Area of ΔORS=5012×(5y˜)×t=5012×5(4)×t=5010t=50t=5∴
Diagram below shows quadrilateral OPQR. The straight line PR intersects the straight line OQ at point S.

It is given that →OP=7x˜, →OR=5y˜, PS:SR=3:1 and →OR is parallel to →PQ.(a) Express in terms of x˜ and y˜,(i) →PR(ii) →OS(b) Using →PQ=m→OR and →SQ=n→OS, where m and n are constants, Find the value of m and of n.(c) Given that |y˜|=4 units and the area of ORS is 50 cm2, find the perpendicular distance from point S to OR.
Solution:
(a)(i)
→PR=→PO+→OR =−7x˜+5y˜
(a)(ii)
→OS=→OP+→PS =7x˜+34→PR =7x˜+34(−7x˜+5y˜) =7x˜−214x˜+154y˜ =74x˜+154y˜
(b)
→PS=→PQ−→SQ34→PR=m→OR−n→OS34(−7x˜+5y˜)=m(5y˜)−n(74x˜+154y˜)−214x˜+154y˜=5my˜−74nx˜−154my˜−214x˜+154y˜=−74nx˜+54my˜−21x˜+15y˜=−7nx˜+5my˜7n=21n=35m=15m=3
(c)
Area of ΔORS=5012×(5y˜)×t=5012×5(4)×t=5010t=50t=5∴