Question 4:
Solution:
(a)
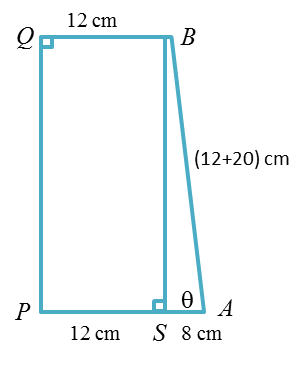
In △BSAcosθ=832=14 θ=1.32 rad (2 d.p.)
(b)
(c)
PQ=√322−82=30.98 cm
Diagram below shows two circles. The larger circle has centre A and radius 20 cm. The smaller circle has centre B and radius 12 cm. The circles touch at point R. The straight line PQ is a common tangent to the circles at point P and point Q.
[Use π = 3.142]
Given that angle PAR = θ radians,
(a) show that θ = 1.32 ( to two decimal places),
(b) calculate the length, in cm, of the minor arc QR,
(c) calculate the area, in cm2, of the shaded region.
Solution:
(a)

In △BSAcosθ=832=14 θ=1.32 rad (2 d.p.)
(b)
Angle QBR = 3.142 – 1.32 = 1.822 rad
Length of minor arc QR
= 12 × 1.822
= 21.86 cm(c)
PQ=√322−82=30.98 cm
Area of the shaded region
= Area of trapezium PQBA– Area of sector QBR – Area of sector PAR
= ½ (12 + 20) (30.98) – ½ (12)2 (1.822) – ½ (20)2(1.32)
= 495.68 – 131.18 – 264
= 100.5 cm2
