Question 7:
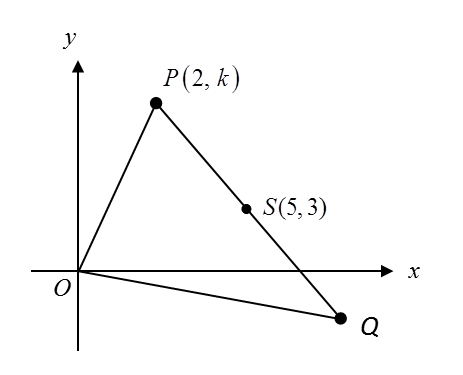
(a) A point Y moves such that its distance from point S is always 5 uints.
Solution:
(a)
The equation of the locus Y (x,y) is given by YS=5 units√(x−5)2+(y−3)2=5x2−10x+25+y2−6y+9=25x2+y2−10x−6y+9=0
(b)(i)
Solutions by scale drawing will not be accepted.
Diagram below shows a triangle OPQ. Point S lies on the line PQ.
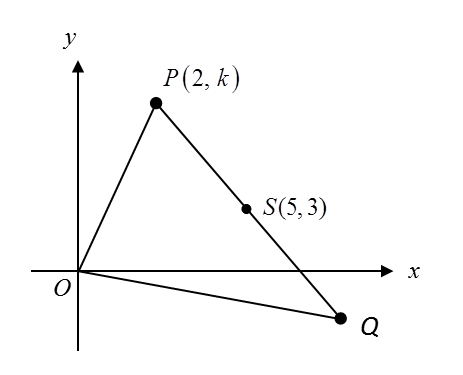
(a) A point Y moves such that its distance from point S is always 5 uints.
Find the equation of the locus of Y.
(b) It is given that point P and point Q lie on the locus of Y .
Calculate
(i) the value of k,
(ii) the coordinates of Q.
(c) Hence, find the area, in uint2, of triangle OPQ.
(c) Hence, find the area, in uint2, of triangle OPQ.
(a)
The equation of the locus Y (x,y) is given by YS=5 units√(x−5)2+(y−3)2=5x2−10x+25+y2−6y+9=25x2+y2−10x−6y+9=0
(b)(i)
Given P (2, k) lies on the locus of Y.
(2)2 + (k)2– 10(2) – 6(k) + 9 = 0
4 + k2– 20 – 6k + 9 = 0
k2 – 6k – 7 = 0
(k – 7) (k + 1) = 0
k = 7 or k = – 1
Based on the diagram, k = 7.
Based on the diagram, k = 7.
(b)(ii)
As P and Q lie on the locus of Y, S is the midpoint of PQ. P = (2, 7), S = (5, 3).
Let the coordinates of Q = (x, y),
(2+x2,7+y2)=(5,3)2+x2=5 and 7+y2=32+x=10 and 7+y=6x=8and y=−1
(c)
Area of △ OPQ=12|0 8 2 0 −1 7 00|=12|0+(8)(7)+0−0−(−1)(2)−0|=12|58|=29 units2
(2+x2,7+y2)=(5,3)2+x2=5 and 7+y2=32+x=10 and 7+y=6x=8and y=−1
Coordinates of point Q = (8, –1).
(c)
Area of △ OPQ=12|0 8 2 0 −1 7 00|=12|0+(8)(7)+0−0−(−1)(2)−0|=12|58|=29 units2