Long Questions (Question 7 & 8)

Posted on May 16, 2020 by Myhometuition

Question 7:

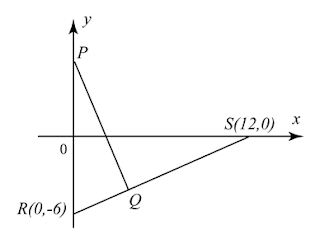
The diagram shows a straight line PQ which meets a straight line RS at the point Q. The point P lies on the y-axis.

(a) Write down the equation of RS in the intercept form.

(b) Given that 2RQ = QS, find the coordinates of Q.

(c) Given that PQ is perpendicular to RS, find the y-intercept of PQ.

Solution:

(a)

Equation of RS

\begin{array}{l} \frac{x}{12} + \frac{y}{- 6} = 1 \\ \frac{x}{12} - \frac{y}{6} = 1 \end{array}

(b)

\begin{array}{l} Given 2 R Q = Q S \\ \frac{R Q}{Q S} = \frac{1}{2} \\ Lets coordinates of Q = (x, y) \\ (\frac{(0) (2) + (12) (1)}{1 + 2}, \frac{(- 6) (2) + (0) (1)}{1 + 2}) = (x, y) \\ x = \frac{12}{3} = 4 \\ y = - \frac{12}{3} = - 4 \\ Q = (4, - 4) \end{array}

(c)

\begin{array}{l} Gradient of R S, m_{R S} \\ = - (\frac{- 6}{12}) = \frac{1}{2} \\ m_{P Q} = - \frac{1}{m_{R S}} = - \frac{1}{\frac{1}{2}} = - 2 \end{array}

Point Q = (4, –4), m = –2

Using y = mx+ c

–4 = –2 (4) + c

c = 4

y–intercept of PQ = 4

Question 8:

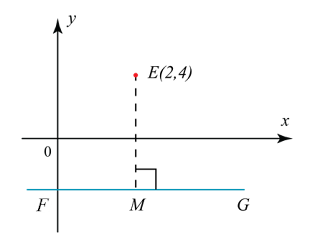
In the diagram, the equation of FMG is y = – 4. A point P moves such that its distance from E is always half of the distance of E from the straight line FG. Find

(a) The equation of the locus of P,

(b) The x-coordinate of the point of intersection of the locus and the x-axis.

Solution:

(a)

Gradient of the straight line FMG = 0

EM is perpendicular to FMG, so gradient of EM also = 0, equation of EM is x = 2

Thus, coordinates of point M = (2, –4).

Let coordinates of point P= (x, y).

Given PE = ½ EM

2PE = EM

2 [(x – 2)²+ (y – 4)²]^½ = [(2 – 2)² + (4 – (–4))²]^½

4 (x² – 4x + 4 + y² – 8y +16) = (0 + 64) → (square for both sides)

4x² – 16x + 16 + 4y² – 32y + 64 = 64

4x² + 4y² – 16x – 32y + 16 = 0

x² + y² – 4x – 8y + 4 = 0

(b)

x² + y² – 4x – 8y + 4 = 0

At x axis, y = 0.

x² + 0 – 4x – 8(0) + 4 = 0

x² – 4x+ 4 = 0

(x – 2) (x – 2) = 0

x = 2

The x-coordinate of the point of intersection of the locus and the x-axis is 2.