Question 8:
Diagram below shows a cyclic quadrilateral PQRS.

(a) Calculate
(i) the length, in cm, of PR,
(ii) ∠PRQ.
(b) Find
(i) the area, in cm2, of ∆ PRS,
(ii) the short distance, in cm, from point S to PR.
Solution:
(a)(i)
PR2=72+82−2(7)(8)cos80oPR2=113−19.4486PR=√93.5514PR=9.6722 cm
(a)(ii)
In cyclic quadrilateral∠PQR+∠PSR=180∠PQR+80=180∠PQR=100osin∠QPR3=sin1009.6722sin∠QPR=0.3055∠QPR=17o47'∠PRQ=180o−100o−17o47' =62o13'
(b)(i)
Area of △PRS=12×7×8sin80o=27.5746 cm2
(b)(ii)
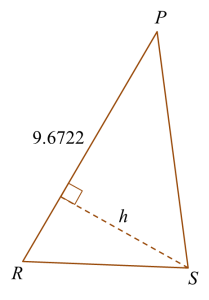
Area of △PRS=27.574612×9.6722×h=27.5746 h=27.5746×29.6722 =5.7018 cmShortest distance=5.7018 cm
Diagram below shows a cyclic quadrilateral PQRS.

(a) Calculate
(i) the length, in cm, of PR,
(ii) ∠PRQ.
(b) Find
(i) the area, in cm2, of ∆ PRS,
(ii) the short distance, in cm, from point S to PR.
Solution:
(a)(i)
PR2=72+82−2(7)(8)cos80oPR2=113−19.4486PR=√93.5514PR=9.6722 cm
(a)(ii)
In cyclic quadrilateral∠PQR+∠PSR=180∠PQR+80=180∠PQR=100osin∠QPR3=sin1009.6722sin∠QPR=0.3055∠QPR=17o47'∠PRQ=180o−100o−17o47' =62o13'
(b)(i)
Area of △PRS=12×7×8sin80o=27.5746 cm2
(b)(ii)

Area of △PRS=27.574612×9.6722×h=27.5746 h=27.5746×29.6722 =5.7018 cmShortest distance=5.7018 cm