Question 10 (10 marks):
Diagram shows a triangle ABC. The straight line AE intersects with the straight line BC at point D. Point V lies on the straight line AE.
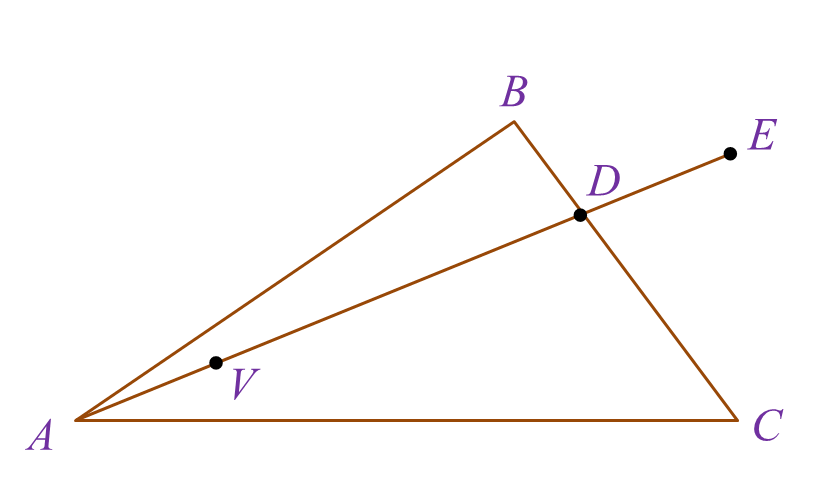
It is given that →BD=13→BC,→AC=6x˜ and →AB=9y˜.(a) Express in terms of x˜ and / or y˜: (i) →BC, (ii) →AD.(b) It is given that →AV=m→AD and →BV=n(x˜−9y˜), where m and n are constants. Find the value of m and of n.(c) Given →AE=hx˜+9y˜, where h is a constant, find the value of h.
Solution:
(a)(i)
→BC=→BA+→AC =−9y˜+6x˜ =6x˜−9y˜
(a)(ii)
→AD=→AB+→BD =9y˜+13→BC =9y˜+13(6x˜−9y˜) =9y˜+2x˜−3y˜ =2x˜+6y˜
(b)
Given →AV=m→AD=m(2x˜+6y˜)=2mx˜+6my˜→AV=→AB+→BV = 9y˜+n(x˜−9y˜) =9y˜+nx˜−9ny˜ =nx˜+(9−9n)y˜By equating the coefficients of x˜ and y˜, 2mx˜+6my˜=nx˜+(9−9n)y˜2m=nn=2m.............(1)6m=9−9n.............(2)Substitute (1) into (2),6m=9−9(2m)6m=9−18m24m=9m=924=38From (1):n=2(38)=34
(c)
A, D and E are collinear.→AD=k(→AE)→AD=k(hx˜+9y˜)2x˜+6y˜=khx˜+9ky˜Equating the coefficients of y˜:9k=6k=69k=23Equating the coefficients of x˜:kh=2(23)h=2h=2×32h=3
Diagram shows a triangle ABC. The straight line AE intersects with the straight line BC at point D. Point V lies on the straight line AE.

It is given that →BD=13→BC,→AC=6x˜ and →AB=9y˜.(a) Express in terms of x˜ and / or y˜: (i) →BC, (ii) →AD.(b) It is given that →AV=m→AD and →BV=n(x˜−9y˜), where m and n are constants. Find the value of m and of n.(c) Given →AE=hx˜+9y˜, where h is a constant, find the value of h.
Solution:
(a)(i)
→BC=→BA+→AC =−9y˜+6x˜ =6x˜−9y˜
(a)(ii)
→AD=→AB+→BD =9y˜+13→BC =9y˜+13(6x˜−9y˜) =9y˜+2x˜−3y˜ =2x˜+6y˜
(b)
Given →AV=m→AD=m(2x˜+6y˜)=2mx˜+6my˜→AV=→AB+→BV = 9y˜+n(x˜−9y˜) =9y˜+nx˜−9ny˜ =nx˜+(9−9n)y˜By equating the coefficients of x˜ and y˜, 2mx˜+6my˜=nx˜+(9−9n)y˜2m=nn=2m.............(1)6m=9−9n.............(2)Substitute (1) into (2),6m=9−9(2m)6m=9−18m24m=9m=924=38From (1):n=2(38)=34
(c)
A, D and E are collinear.→AD=k(→AE)→AD=k(hx˜+9y˜)2x˜+6y˜=khx˜+9ky˜Equating the coefficients of y˜:9k=6k=69k=23Equating the coefficients of x˜:kh=2(23)h=2h=2×32h=3