Question 9 (10 marks):
Diagram 5 shows triangles OAQ and OPB where point P lies on OA and point Q lies on OB. The straight lines AQ and PB intersect at point R.
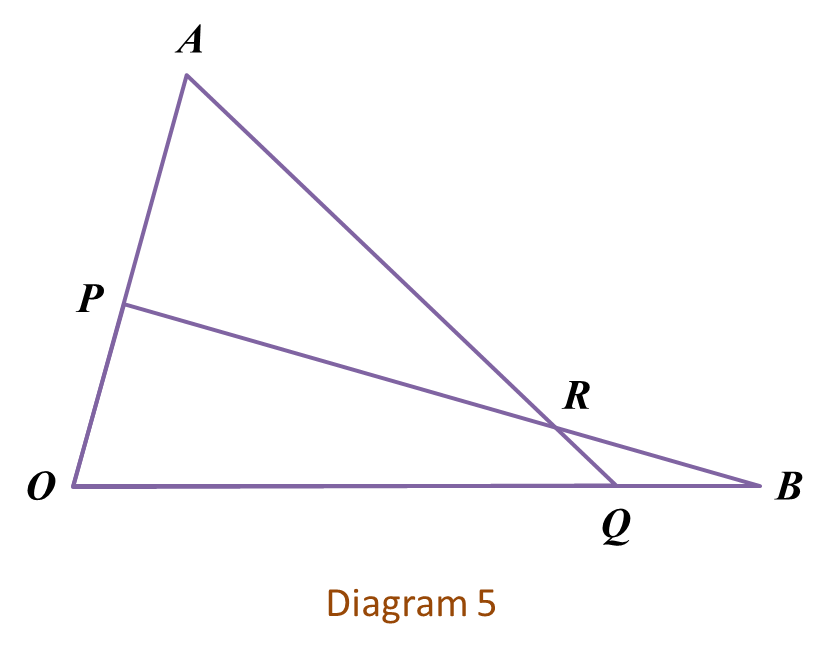 It is given that →OA=18x˜, →OB=16y˜, OP:PA=1:2, OQ:QB=3:1,→PR=m→PB and →QR=n→QA, where m and n are constants.(a) Express →OR in terms of (i) m, x˜ and y˜, (ii) n, x˜ and y˜,(b) Hence, find the value of m and of n.(c) Given |x˜|=2 units, |y˜|=1 unit and OA is perpendicular to OB calculate |→PR|.
It is given that →OA=18x˜, →OB=16y˜, OP:PA=1:2, OQ:QB=3:1,→PR=m→PB and →QR=n→QA, where m and n are constants.(a) Express →OR in terms of (i) m, x˜ and y˜, (ii) n, x˜ and y˜,(b) Hence, find the value of m and of n.(c) Given |x˜|=2 units, |y˜|=1 unit and OA is perpendicular to OB calculate |→PR|.
Solution:
(a)(i)
→OR=→OP+→PR =13→OA+m→PB =13(18x˜)+m(→PO+→OB) =6x˜+m(−6x˜+16y˜)
(a)(ii)
→OR=→OQ+→QR =34→OB+n→QA =34(16y˜)+n(→QO+→OA) =12y˜+n(−12y˜+18x˜) =(12−12n)y˜+18nx˜
(b)
6x˜+m(−6x˜+16y˜)=(12−12n)y˜+18nx˜6x˜−6mx˜+16my˜=18nx˜+12y˜−12ny˜by comparison;6−6m=18n1−m=3nm=1−3n..............(1)16m=12−12n4m=3−3n..............(2)Substitute (1) into (2),4(1−3n)=3−3n4−12n=3−3n9n=1n=19Substitute n=19 into (1),m=1−3(19)m=23
[adinserter block="3"]
(c)
|x˜|=2, |y˜|=1 →PR=23→PB =23(−6x˜+16y˜) =−4x˜+323y˜|→PR|=√[−4(2)]2+[323(1)]2 =√16009 =403 units
Diagram 5 shows triangles OAQ and OPB where point P lies on OA and point Q lies on OB. The straight lines AQ and PB intersect at point R.
 It is given that →OA=18x˜, →OB=16y˜, OP:PA=1:2, OQ:QB=3:1,→PR=m→PB and →QR=n→QA, where m and n are constants.(a) Express →OR in terms of (i) m, x˜ and y˜, (ii) n, x˜ and y˜,(b) Hence, find the value of m and of n.(c) Given |x˜|=2 units, |y˜|=1 unit and OA is perpendicular to OB calculate |→PR|.
It is given that →OA=18x˜, →OB=16y˜, OP:PA=1:2, OQ:QB=3:1,→PR=m→PB and →QR=n→QA, where m and n are constants.(a) Express →OR in terms of (i) m, x˜ and y˜, (ii) n, x˜ and y˜,(b) Hence, find the value of m and of n.(c) Given |x˜|=2 units, |y˜|=1 unit and OA is perpendicular to OB calculate |→PR|.
Solution:
(a)(i)
→OR=→OP+→PR =13→OA+m→PB =13(18x˜)+m(→PO+→OB) =6x˜+m(−6x˜+16y˜)
(a)(ii)
→OR=→OQ+→QR =34→OB+n→QA =34(16y˜)+n(→QO+→OA) =12y˜+n(−12y˜+18x˜) =(12−12n)y˜+18nx˜
(b)
6x˜+m(−6x˜+16y˜)=(12−12n)y˜+18nx˜6x˜−6mx˜+16my˜=18nx˜+12y˜−12ny˜by comparison;6−6m=18n1−m=3nm=1−3n..............(1)16m=12−12n4m=3−3n..............(2)Substitute (1) into (2),4(1−3n)=3−3n4−12n=3−3n9n=1n=19Substitute n=19 into (1),m=1−3(19)m=23
[adinserter block="3"]
(c)
|x˜|=2, |y˜|=1 →PR=23→PB =23(−6x˜+16y˜) =−4x˜+323y˜|→PR|=√[−4(2)]2+[323(1)]2 =√16009 =403 units