Question 10 (7 marks):
Solution by scale drawing is not accepted.
Diagram shows the locations of town M and town N drawn on a Cartesian plane.
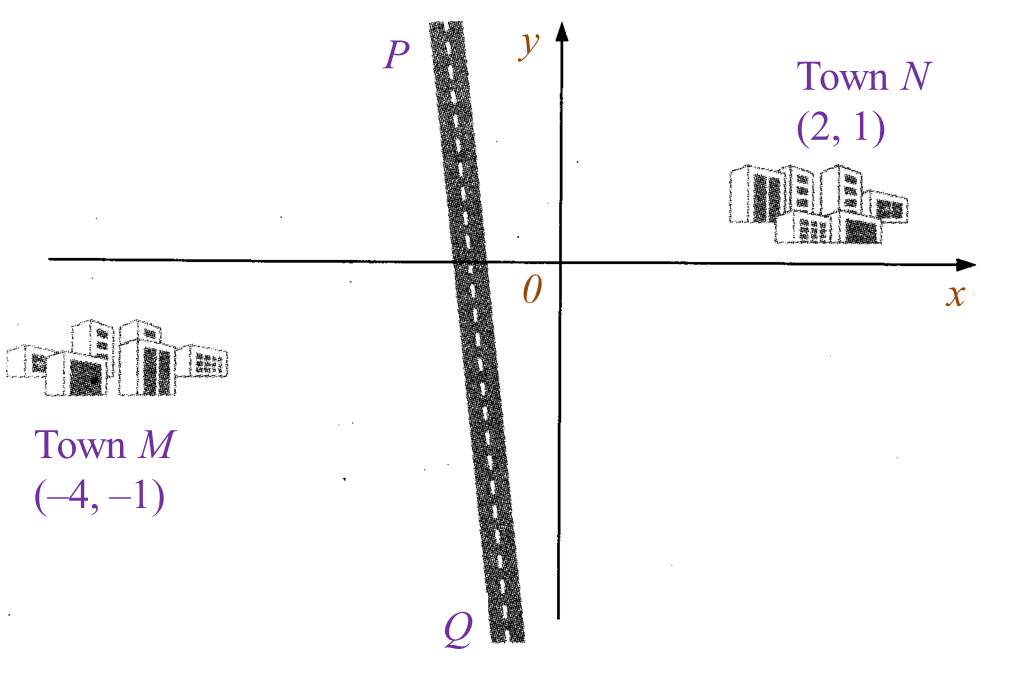
PQ is a straight road such that the distance from town M and town N to any point on the road is always equal.
(a) Find the equation of PQ.
(b) Another straight road, ST with an equation y = 2x + 7 is to be built.
(i) A traffic light is to be installed at the crossroads of the two roads.
Find the coordinates of the traffic light.
(ii) Which of the two roads passes through town L (−43,1)?
Solution:
(a)
T(x,y) is a point on PQ.TM=TN√[x−(−4)2]+[y−(−1)]2=√(x−2)2+(y−1)2√(x+4)2+(y+1)2=√(x−2)2+(y−1)2(x+4)2+(y+1)2=(x−2)2+(y−1)2x2+8x+16+y2+2y+1=x2−4x+4+y2−2y+18x+2y+17+4x+2y−5=012x+4y+12=03x+y+3=0Equation of PQ:3x+y+3=0
(b)(i)
y=2x+7 ............ (1)3x+y+3=0 ............ (2)Substitute (1) into (2):3x+2x+7+3=05x=−10x=−2When x=−2,From (1),y=2(−2)+7=3Coordinates of traffic light=(−2,3).
(b)(ii)
L(−43,1):x=−43,y=1The equation of ST:y=2x+7Left hand side: y=1Right hand side: 2(−43)+7=413Thus, the road y=2x+7 does not pass through L.The equation of PQ:3x+y+3=0Left hand side: 3x+y+3=3(−43)+1+3 =−4+4=0Right hand side=0Left hand side=Right hand sideThus, the road 3x+y+3=0passes through L.
Solution by scale drawing is not accepted.
Diagram shows the locations of town M and town N drawn on a Cartesian plane.

PQ is a straight road such that the distance from town M and town N to any point on the road is always equal.
(a) Find the equation of PQ.
(b) Another straight road, ST with an equation y = 2x + 7 is to be built.
(i) A traffic light is to be installed at the crossroads of the two roads.
Find the coordinates of the traffic light.
(ii) Which of the two roads passes through town L (−43,1)?
Solution:
(a)
T(x,y) is a point on PQ.TM=TN√[x−(−4)2]+[y−(−1)]2=√(x−2)2+(y−1)2√(x+4)2+(y+1)2=√(x−2)2+(y−1)2(x+4)2+(y+1)2=(x−2)2+(y−1)2x2+8x+16+y2+2y+1=x2−4x+4+y2−2y+18x+2y+17+4x+2y−5=012x+4y+12=03x+y+3=0Equation of PQ:3x+y+3=0
(b)(i)
y=2x+7 ............ (1)3x+y+3=0 ............ (2)Substitute (1) into (2):3x+2x+7+3=05x=−10x=−2When x=−2,From (1),y=2(−2)+7=3Coordinates of traffic light=(−2,3).
(b)(ii)
L(−43,1):x=−43,y=1The equation of ST:y=2x+7Left hand side: y=1Right hand side: 2(−43)+7=413Thus, the road y=2x+7 does not pass through L.The equation of PQ:3x+y+3=0Left hand side: 3x+y+3=3(−43)+1+3 =−4+4=0Right hand side=0Left hand side=Right hand sideThus, the road 3x+y+3=0passes through L.