Long Questions (Question 10)

Question 10 (8 marks):
Diagram shows a circle and a sector of a circle with a common centre O. The radius of the circle is r cm.


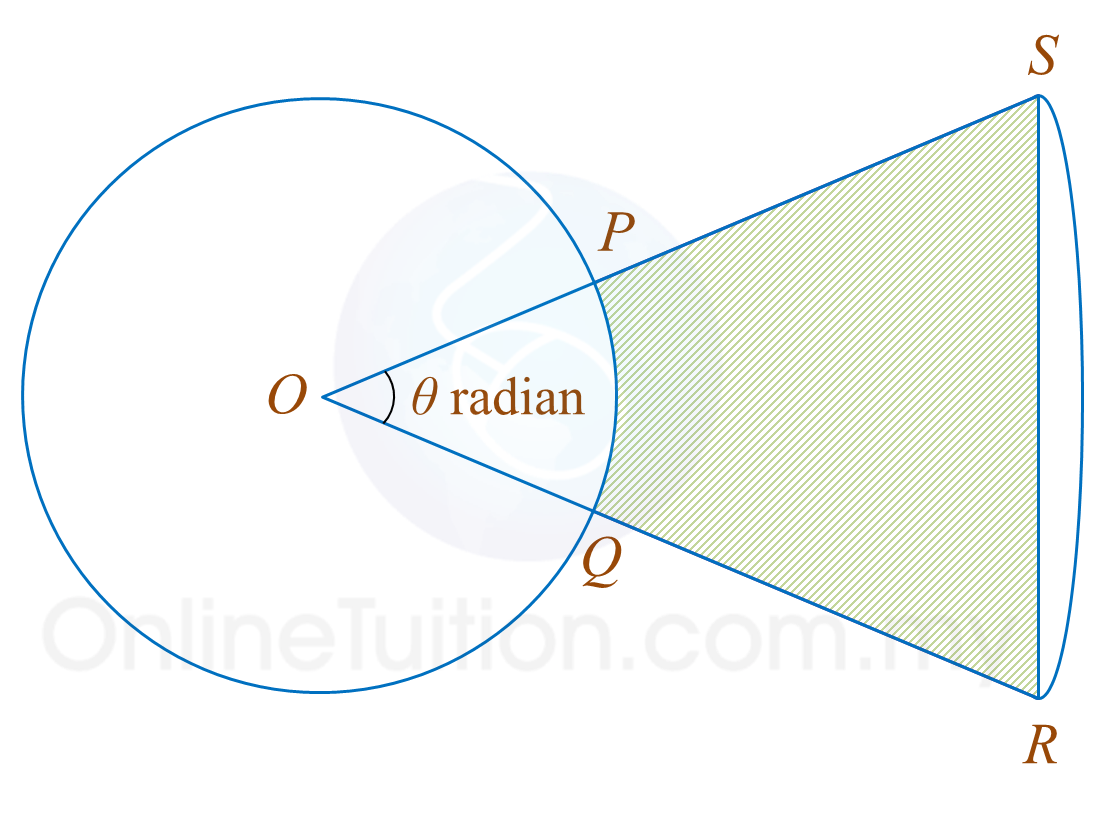
It is given that the length of arc PQ and arc RS are 2 cm and 7 cm respectively. QR = 10 cm.
[Use θ = 3.142]
Find
(a) the value of r and of θ,
(b) the area, in cm², of the shaded region.


Solution:
(a)
$\begin{array}{l}\text{Length of arc }PQ=2\text{ cm}\\ r\theta =2\mathrm{.................}\left(1\right)\\ \\ \text{Length of arc }RS=7\text{ cm}\\ \left(r+10\right)\theta =7\\ r\theta +10\theta =7\mathrm{.................}\left(2\right)\\ \\ \text{Substitute }\left(1\right)\text{ into }\left(2\right):\\ 2+10\theta =7\\ 10\theta =5\\ \theta =\frac{5}{10}\\ \theta =0.5\text{ rad}\\ \\ \text{From}\left(1\right):\\ \text{When }\theta =0.5\text{ rad,}\\ r\times 0.5=2\\ r=4\end{array}$

(b)
$\begin{array}{l}OS=OR=4+10=14\text{ cm}\\ \text{Area of shaded region}\\ =\text{area of }\Delta ORS-\text{ area of sector }OPQ\\ =\left(\frac{1}{2}\times {14}^2\times \sin 0.5\text{ rad}\right)-\left(\frac{1}{2}\times 4^2\times 0.5\right)\\ =42.981{\text{ cm}}^2\end{array}$