Long Questions (Question 7)

Question 7:
In a boarding school entry exam, 300 students sat for a mathematics test. The marks obtained follow a normal distribution with a mean of 56 and a standard deviation of 8.

(a) Find the number of students who pass the test if the passing mark is 40.

(b) If 12% of the students pass the test with grade A, find the minimum mark to obtain grade A.

Solution:
$\begin{array}{l}\text{Let }X=\text{marks obtained by students}\\ X~N\left(56,8^2\right)\\ \left(a\right)P\left(X\ge 40\right)=P\left(Z\ge \frac{40-56}{8}\right)\\ =P\left(Z\ge -2\right)\\ =1-P\left(Z\ge 2\right)\\ =1-0.02275\\ =0.9773\\ \text{Number of students who pass the test}\\ =0.9773\times 300\\ =293\\ \\ \left(b\right)\text{ Let the minimum mark to obtain grade }A\text{ be }k\\ P\left(X\ge k\right)=0.12\\ P\left(Z\ge \frac{k-56}{8}\right)=0.12\\ \frac{k-56}{8}=1.17\\ k=\left(1.17\right)\left(8\right)+56\\ =65.36\end{array}$

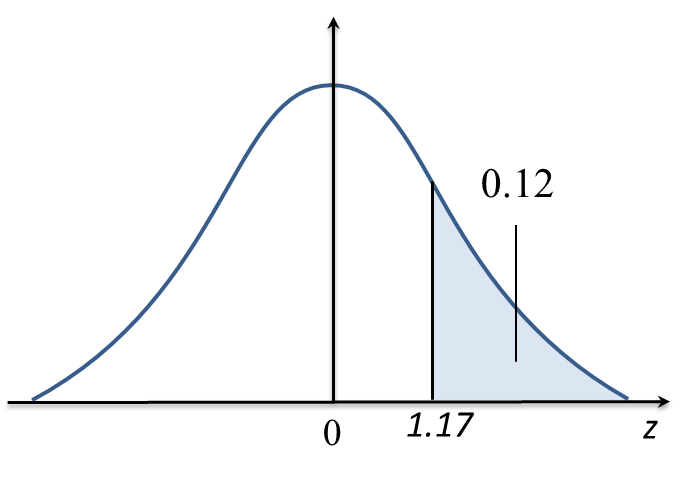Thus, the minimum mark to obtain grade A is 66.