Question 9 (6 marks):
Solution by scale drawing is not accepted.
Diagram shows a triangle OCD.
 Diagram
Diagram
(a) Given the area of triangle OCD is 30 units2, find the value of h.
(b) Point Q (2, 4) lies on the straight line CD.
(i) Find CQ : QD.
(ii) Point P moves such that PD = 2 PQ.
Find the equation of the locus P.
Solution:
(a)
Given Area of △ OCD = 3012 |0 h−6 0 2 8 00|=30|(0)(2)+(h)(8)+(−6)(0)−(0)(h)−(2)(−6)−(8)(0)|=60|0+8h+0−0+12−0|=60|8h+12|=608h+12=608h=48h=6or 8h+12=−608h=−72h=−9(ignore)
(b)(i)
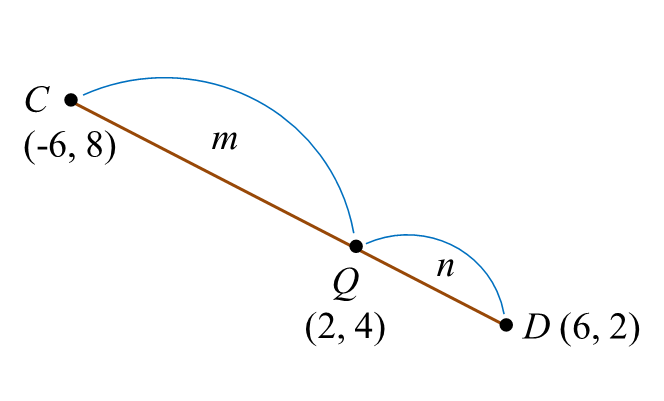
[6(m)+(−6)(n)m+n, 2(m)+(8)(n)m+n]=(2, 4)6m−6nm+n=26m−6n=2m+2n4m=8nmn=84mn=212m+8nm+n=42m+8n=4m+4n2m=4nmn=42mn=21Thus, CQ=QD=2:1
(b)(ii)
PD=2PQ√(x−6)2+(y−2)2=2√(x−2)2+(y−4)2(x−6)2+(y−2)2=4[(x−2)2+(y−4)2]x2−12x+36+y2−4y+4=4[x2−4x+4+y2−8y+16]x2−12x+36+y2−4y+4=4x2−16x+16+4y2−32y+64The equation of locus P:3x2+3y2−4x−28y+40=0
Solution by scale drawing is not accepted.
Diagram shows a triangle OCD.
 Diagram
Diagram(a) Given the area of triangle OCD is 30 units2, find the value of h.
(b) Point Q (2, 4) lies on the straight line CD.
(i) Find CQ : QD.
(ii) Point P moves such that PD = 2 PQ.
Find the equation of the locus P.
Solution:
(a)
Given Area of △ OCD = 3012 |0 h−6 0 2 8 00|=30|(0)(2)+(h)(8)+(−6)(0)−(0)(h)−(2)(−6)−(8)(0)|=60|0+8h+0−0+12−0|=60|8h+12|=608h+12=608h=48h=6or 8h+12=−608h=−72h=−9(ignore)
(b)(i)

[6(m)+(−6)(n)m+n, 2(m)+(8)(n)m+n]=(2, 4)6m−6nm+n=26m−6n=2m+2n4m=8nmn=84mn=212m+8nm+n=42m+8n=4m+4n2m=4nmn=42mn=21Thus, CQ=QD=2:1
(b)(ii)
PD=2PQ√(x−6)2+(y−2)2=2√(x−2)2+(y−4)2(x−6)2+(y−2)2=4[(x−2)2+(y−4)2]x2−12x+36+y2−4y+4=4[x2−4x+4+y2−8y+16]x2−12x+36+y2−4y+4=4x2−16x+16+4y2−32y+64The equation of locus P:3x2+3y2−4x−28y+40=0