Question 5 (10 marks):
(a) Prove sin(3x+π6)−sin(3x−π6)=cos3x(b) Hence,(i) solve the equation sin(3x2+π6)−sin(3x2−π6)=12 for 0≤x≤2π and give your answer in the simplest fraction form in terms of π radian.(ii) sketch the graph of y=sin(3x+π6)−sin(3x−π6)−12 for 0≤x≤π.
Solution:
(a) Left hand side,sin(3x+π6)−sin(3x−π6)=[sin3xcosπ6+cos3xsinπ6]−[sin3xcosπ6−cos3xsinπ6]=2[cos3xsinπ6]=2[cos3x(12)]=cos3x(right hand side)
(b)(i)sin(3x2+π6)−sin(3x2−π6)=12,0≤x≤2πcos3x2=123x2=π3,(2π−π3),(2π+π3)3x2=π3,5π3,7π3x=2π9,10π9,14π9
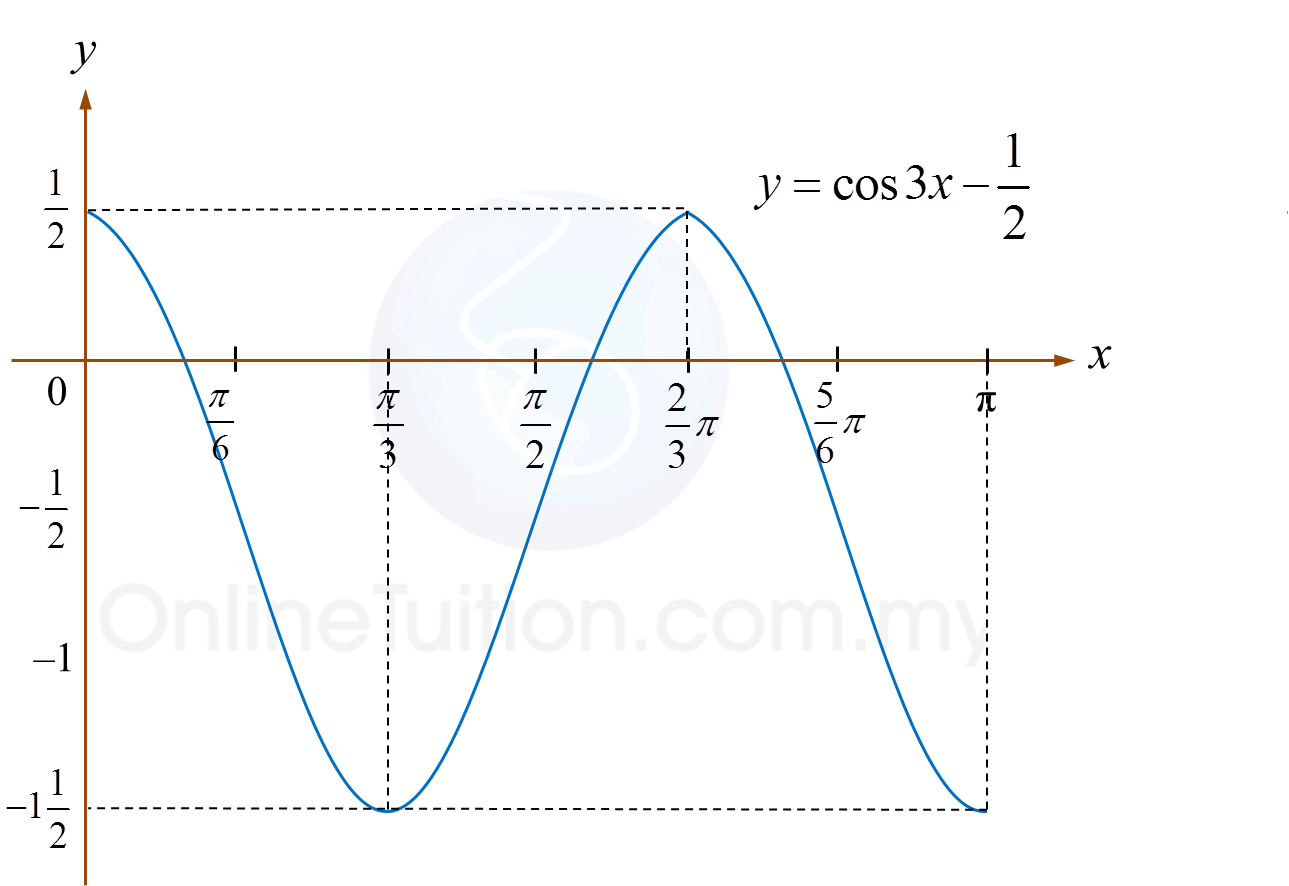
(b)(ii) y=sin(3x+π6)−sin(3x−π6)−12 for 0≤x≤π.y=cos3x−12
(a) Prove sin(3x+π6)−sin(3x−π6)=cos3x(b) Hence,(i) solve the equation sin(3x2+π6)−sin(3x2−π6)=12 for 0≤x≤2π and give your answer in the simplest fraction form in terms of π radian.(ii) sketch the graph of y=sin(3x+π6)−sin(3x−π6)−12 for 0≤x≤π.
Solution:
(a) Left hand side,sin(3x+π6)−sin(3x−π6)=[sin3xcosπ6+cos3xsinπ6]−[sin3xcosπ6−cos3xsinπ6]=2[cos3xsinπ6]=2[cos3x(12)]=cos3x(right hand side)
(b)(i)sin(3x2+π6)−sin(3x2−π6)=12,0≤x≤2πcos3x2=123x2=π3,(2π−π3),(2π+π3)3x2=π3,5π3,7π3x=2π9,10π9,14π9
(b)(ii) y=sin(3x+π6)−sin(3x−π6)−12 for 0≤x≤π.y=cos3x−12
