Question 6 (10 marks):
(a) Prove that 2 tan x cos2 x = sin 2x.
(b) Hence, solve the equation 4 tan x cos2 x = 1 for 0 ≤ x ≤ 2π.
(c)(i) Sketch the graph of y = sin 2x for 0 ≤ x ≤ 2π.
(c)(ii) Hence, using the same axes, sketch a suitable straight line to find the number of solutions for the equation 4π tan x cos2 x = x – 2π for 0 ≤ x ≤ 2π.
State the number of solutions.
Solution:
(a)
2tanxcos2x=sin2xLeft hand side=2tanxcos2x=2×sinxcosx×cos2x=2sinxcosx=sin2x= Right hand side (Proven)
(b)
4tanxcos2x=1, 0≤x≤2π2(2tanxcos2x)=12sin2x=1sin2x=12Basic angle=π62x=π6,(π−π6),(2π+π6),(3π−π6)2x=π6,5π6,13π6,17π6x=π12,5π12,13π12,17π12
(c)(i)
y = sin 2x, 0 ≤ x ≤ 2π.
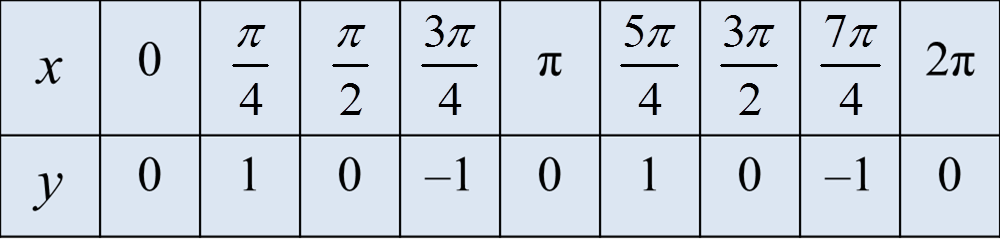
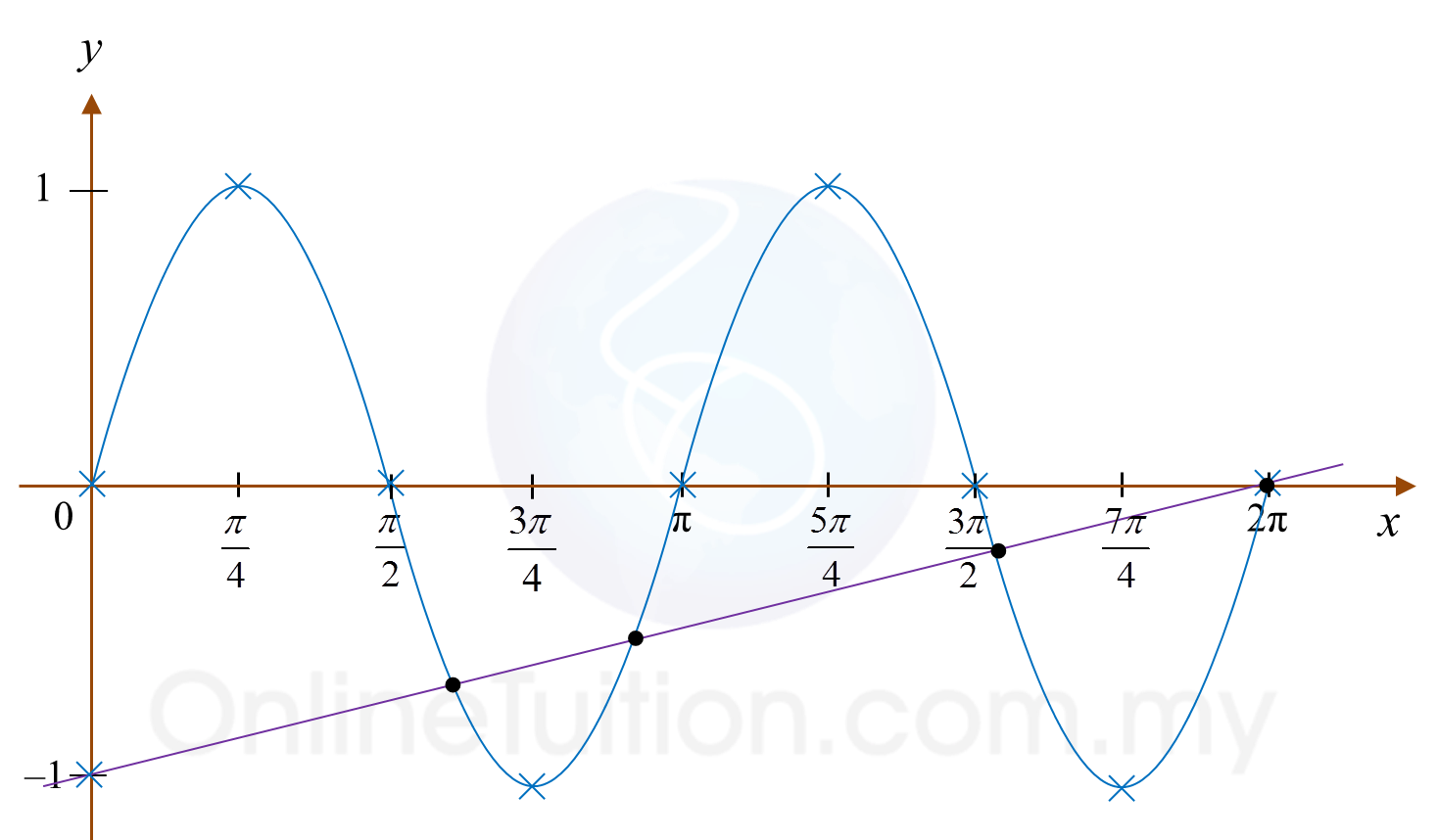
(c)(ii)
4πtanxcos2x=x−2π2π(2tanxcos2x)=x−2π2πsin2x=x−2πsin2x=x2π−2π2πsin2x=x2π−1y=x2π−1
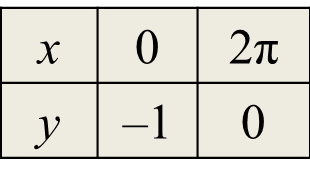
Number of solutions = 4
(a) Prove that 2 tan x cos2 x = sin 2x.
(b) Hence, solve the equation 4 tan x cos2 x = 1 for 0 ≤ x ≤ 2π.
(c)(i) Sketch the graph of y = sin 2x for 0 ≤ x ≤ 2π.
(c)(ii) Hence, using the same axes, sketch a suitable straight line to find the number of solutions for the equation 4π tan x cos2 x = x – 2π for 0 ≤ x ≤ 2π.
State the number of solutions.
Solution:
(a)
2tanxcos2x=sin2xLeft hand side=2tanxcos2x=2×sinxcosx×cos2x=2sinxcosx=sin2x= Right hand side (Proven)
(b)
4tanxcos2x=1, 0≤x≤2π2(2tanxcos2x)=12sin2x=1sin2x=12Basic angle=π62x=π6,(π−π6),(2π+π6),(3π−π6)2x=π6,5π6,13π6,17π6x=π12,5π12,13π12,17π12

(c)(i)
y = sin 2x, 0 ≤ x ≤ 2π.


(c)(ii)
4πtanxcos2x=x−2π2π(2tanxcos2x)=x−2π2πsin2x=x−2πsin2x=x2π−2π2πsin2x=x2π−1y=x2π−1

Number of solutions = 4