Question 9 (10 marks):
Solution by scale drawing is not accepted.
Diagram shows a transparent prism with a rectangular base PQRS. The inclined surface PQUT is a square with sides 12 cm and the inclined surface RSTU is a rectangle. PTS is a uniform cross section of the prism. QST is a green coloured plane in the prism.

It is given that ∠PST = 37o and ∠TPS = 45o.
Find
(a) the length, in cm, of ST,
(b) the area, in cm2, of the green coloured plane.
(c) the shortest length, in cm, from point T to the straight line QS.
Solution:
(a)
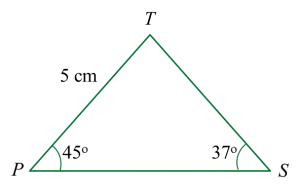
STsin45o=12sin37oST=12sin37o×sin45oST=14.1 cm
(b)
QT2=QP2+PT2QT2=122+122QT=√122+122=16.97 cm∠PTS=180o−45o−37o=98oPSsin98o=12sin37oPS=12sin37o×sin98oPS=19.75 cmQS2=QP2+PS2QS=√QP2+PS2QS=√122+19.752QS=23.11 cm
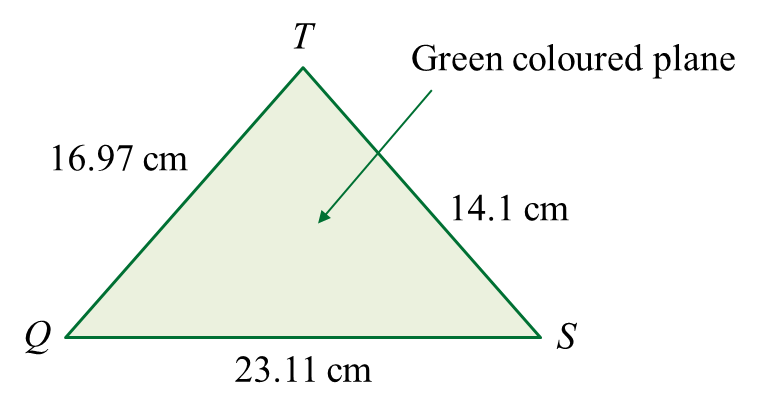
QS2=QT2+ST2−2(QT)(ST)cos∠QTS23.112=16.972+14.12−2(16.97)(14.1)cos∠QTScos∠QTS=16.972+14.12−23.1122(16.97)(14.1)cos∠QTS=−47.28478.55∠QTS=95.67oThus, area of green coloured plane QTS=12(16.97)(14.1)sin95.67o=119.05 cm2
(c)
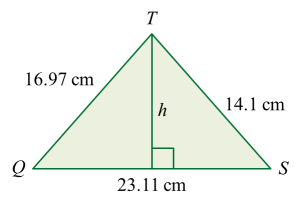
Let the shortest length from point Tto the straight line QS is h.Area of ΔQTS=119.0512(h)(23.11)=119.05h=10.3 cm
Solution by scale drawing is not accepted.
Diagram shows a transparent prism with a rectangular base PQRS. The inclined surface PQUT is a square with sides 12 cm and the inclined surface RSTU is a rectangle. PTS is a uniform cross section of the prism. QST is a green coloured plane in the prism.

It is given that ∠PST = 37o and ∠TPS = 45o.
Find
(a) the length, in cm, of ST,
(b) the area, in cm2, of the green coloured plane.
(c) the shortest length, in cm, from point T to the straight line QS.
Solution:
(a)

STsin45o=12sin37oST=12sin37o×sin45oST=14.1 cm
(b)
QT2=QP2+PT2QT2=122+122QT=√122+122=16.97 cm∠PTS=180o−45o−37o=98oPSsin98o=12sin37oPS=12sin37o×sin98oPS=19.75 cmQS2=QP2+PS2QS=√QP2+PS2QS=√122+19.752QS=23.11 cm

QS2=QT2+ST2−2(QT)(ST)cos∠QTS23.112=16.972+14.12−2(16.97)(14.1)cos∠QTScos∠QTS=16.972+14.12−23.1122(16.97)(14.1)cos∠QTS=−47.28478.55∠QTS=95.67oThus, area of green coloured plane QTS=12(16.97)(14.1)sin95.67o=119.05 cm2
(c)

Let the shortest length from point Tto the straight line QS is h.Area of ΔQTS=119.0512(h)(23.11)=119.05h=10.3 cm