Question 14 (3 marks):
It is given that ∫5(2x+3)ndx=p(2x+3)5+c , where c, n and p are constants.
Find the value of n and of p.
Solution:
∫5(2x+3)ndx=∫5(2x+3)−ndx=5(2x+3)−n+1(−n+1)×2+c=52(1−n)×1(2x+3)n−1+c=52(1−n)(2x+3)n−1+cCompare 52(1−n)(2x+3)n−1with p(2x+3)5n−1=5n=652(1−n)=p52(1−6)=p52(−5)=pp=−12
It is given that ∫5(2x+3)ndx=p(2x+3)5+c , where c, n and p are constants.
Find the value of n and of p.
Solution:
∫5(2x+3)ndx=∫5(2x+3)−ndx=5(2x+3)−n+1(−n+1)×2+c=52(1−n)×1(2x+3)n−1+c=52(1−n)(2x+3)n−1+cCompare 52(1−n)(2x+3)n−1with p(2x+3)5n−1=5n=652(1−n)=p52(1−6)=p52(−5)=pp=−12
Question 15 (4 marks):
Diagram shows the curve y = g(x). The straight line is a tangent to the curve.
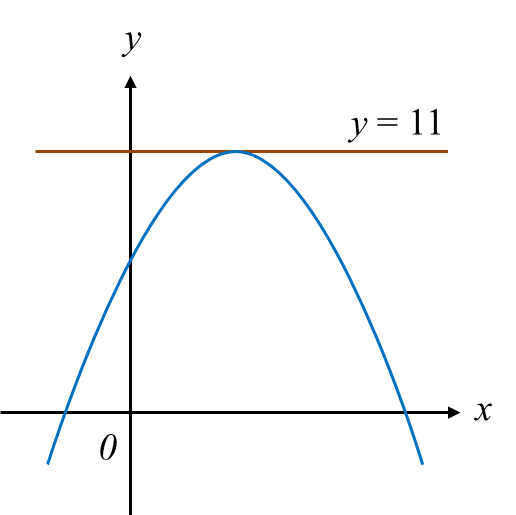 Diagram
Diagram
Given g’(x) = –4x + 8, find the equation of the curve.
Solution:
Given g'
Diagram shows the curve y = g(x). The straight line is a tangent to the curve.
 Diagram
DiagramGiven g’(x) = –4x + 8, find the equation of the curve.
Solution:
Given g'