Question 8 (3 marks):
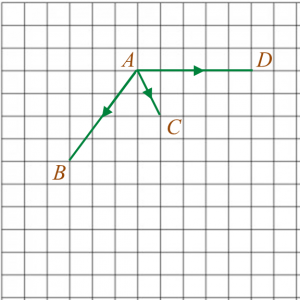
Diagram shows vectors →AB, →AC and →AD drawn on a square grid with sides of 1 unit.
 Diagram
Diagram
(a) Find |−→BA|.(b) Given →AB=b˜ and →AC=c˜,express in terms of b˜ and c˜ (i) →BC,(ii) →AD
Solution:
(a)
|−→BA|=√32+42=5 units
(b)(i)
→BC=→BA+→AC =−b˜+c˜ =c˜−b˜
(b)(ii)
→AD=→AB+→BD =b˜+2→BC =b˜+2(c˜−b˜) =2c˜−b˜
Diagram shows vectors →AB, →AC and →AD drawn on a square grid with sides of 1 unit.
 Diagram
Diagram(a) Find |−→BA|.(b) Given →AB=b˜ and →AC=c˜,express in terms of b˜ and c˜ (i) →BC,(ii) →AD
Solution:
(a)
|−→BA|=√32+42=5 units
(b)(i)
→BC=→BA+→AC =−b˜+c˜ =c˜−b˜
(b)(ii)
→AD=→AB+→BD =b˜+2→BC =b˜+2(c˜−b˜) =2c˜−b˜
Question 9 (3 marks):
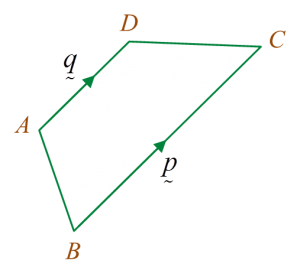
Diagram shows a trapezium ABCD.
 Diagram
Diagram
Given p˜=(34) and q˜=(k−1 2), where k is a constant, find value of k.
Solution:
p˜=mq˜(34)=m(k−1 2)(34)=(mk−m 2m)mk−m=3 .......... (1)2m=4 ................ (2)From(2):2m=4m=2Substitute m=2 into (1):2k−2=32k=3+22k=5k=52
Diagram shows a trapezium ABCD.
 Diagram
DiagramGiven p˜=(34) and q˜=(k−1 2), where k is a constant, find value of k.
Solution:
p˜=mq˜(34)=m(k−1 2)(34)=(mk−m 2m)mk−m=3 .......... (1)2m=4 ................ (2)From(2):2m=4m=2Substitute m=2 into (1):2k−2=32k=3+22k=5k=52