Short Questions (Question 5 & 6)

Question 5 (4 marks):
Diagram shows a circle with centre O.

Diagram

PR and QR are tangents to the circle at points P and Q respectively. It is given that the length of minor arc PQ is 4 cm and $OR=\frac{5}{\alpha }\text{ cm}\text{.}$  
Express in terms of α,
(a) the radius, r, of the circle,
(b) the area, A, of the shaded region.

Solution:
(a)
$\begin{array}{l}\text{Given }{s}_{PQ}=4\\ r\alpha =4\\ r=\frac{4}{\alpha }\text{ cm}\end{array}$

(b)

$\begin{array}{l}PR=\sqrt{{\left(\frac{5}{\alpha }\right)}^2-{\left(\frac{4}{\alpha }\right)}^2}\\ PR=\sqrt{\frac{9}{{\alpha }^2}}\\ PR=\frac{3}{\alpha }\\ \\ A=\text{ Area of shaded region}\\ A=\text{ Area of quadrilateral }OPRQ-\\ \text{Area of sector }OPQ\\ =2\left(\text{Area of }△OPR\right)-\frac{1}{2}{r}^2\theta \\ =2\left[\frac{1}{2}\times \frac{3}{\alpha }\times \frac{4}{\alpha }\right]-\left[\frac{1}{2}\times {\left(\frac{4}{\alpha }\right)}^2\times \alpha \right]\\ =\frac{12}{{\alpha }^2}-\frac{8}{\alpha }\\ =\frac{12-8\alpha }{{\alpha }^2}{\text{ cm}}^2\end{array}$

Question 6 (3 marks):
Diagram shows two sectors AOD and BOC of two concentric circles with centre O.

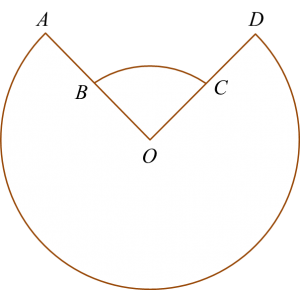Diagram

The angle subtended at the centre O by the major arc AD is 7α radians and the perimeter of the whole diagram is 50 cm.
Given OB = r cm, OA = 2OB and ∠BOC = 2α, express r in terms of α.

Solution:

$\begin{array}{l}\text{Length of major arc }AOD\\ =2r\times 7\alpha \\ =14r\alpha \\ \\ \text{Length of minor arc }BOC\\ =r\times 2\alpha \\ =2r\alpha \\ \\ \text{Perimeter of the whole diagram}\\ =50\text{ cm}\\ 14r\alpha +2r\alpha +r+r=50\\ 16r\alpha +2r=50\\ 8r\alpha +r=25\\ r\left(8\alpha +1\right)=25\\ r=\frac{25}{8\alpha +1}\end{array}$