Question 8 (3 marks):
The following information refers to the equation of two straight lines, AB and CD.
AB:y−2kx−3=0 CD:x3h+y4=1where h and k are constants.
Given the straight lines AB and CD are perpendicular to each other, express h in terms of k.
Solution:
AB:y−2kx−3=0y=2kx+3mAB=2kCD:x3h+y4=1mCD=−43hmAB×mCD=−12k×(−43h)=−1−8k=−3hh=83k
The following information refers to the equation of two straight lines, AB and CD.
AB:y−2kx−3=0 CD:x3h+y4=1where h and k are constants.
Given the straight lines AB and CD are perpendicular to each other, express h in terms of k.
Solution:
AB:y−2kx−3=0y=2kx+3mAB=2kCD:x3h+y4=1mCD=−43hmAB×mCD=−12k×(−43h)=−1−8k=−3hh=83k
Question 9 (3 marks):
A straight line passes through P(3, 1) and Q(12, 7). The point R divides the line segment PQ such that 2PQ = 3RQ.
Find the coordinates of R.
Solution:
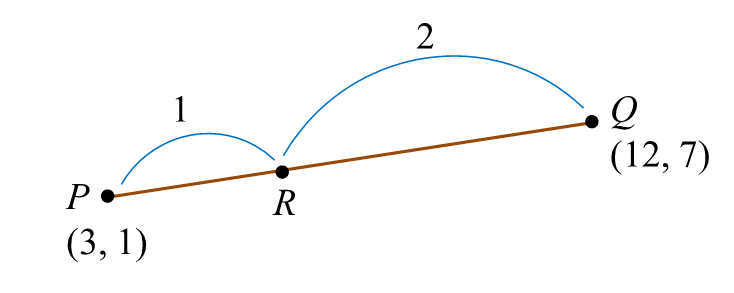
2PQ=3RQPQRQ=32Point R=(1(12)+2(3)1+2,1(7)+2(1)1+2)=(183,93)=(6,3)
A straight line passes through P(3, 1) and Q(12, 7). The point R divides the line segment PQ such that 2PQ = 3RQ.
Find the coordinates of R.
Solution:

2PQ=3RQPQRQ=32Point R=(1(12)+2(3)1+2,1(7)+2(1)1+2)=(183,93)=(6,3)