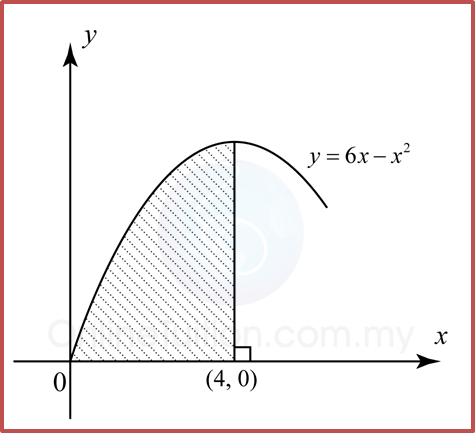
3.5.1 Integration as the Summation of Areas – Examples

Example 1
Find the area of the shaded region.

Solution:

\begin{array}{l} Area of the shaded region \\ = \int_{a}^{b} y d x \\ = \int_{0}^{4} (6 x - x^{2}) d x \\ = {[\frac{6 x^{2}}{2} - \frac{x^{3}}{3}]}_{0}^{4} \\ = [3 {(4)}^{2} - \frac{{(4)}^{3}}{3}] - 0 \\ = 26 \frac{2}{3} {unit}^{2} \end{array}

Example 2
Find the area of the shaded region.

Solution:

y = x -----(1)

x = 8y – y²-----(2)

Substitute (1) into (2),

y = 8y – y²

y²– 7y = 0

y (y – 7) = 0

y = 0 or 7

From (1), x = 0 or 7

Therefore the intersection points of the curve and the straight line is (0, 0) and (7, 7).

Intersection point of the curve and y-axis is,

x = 8y – y²

At y-axis, x = 0

0 = 8y – y²

y (y – 8) = 0

y = 0, 8

Area of shaded region = (A₁) Area of triangle + (A₂) Area under the curve from y = 7 to y = 8.

\begin{array}{l} = \frac{1}{2} \times base \times height + \int_{7}^{8} x d y \\ = \frac{1}{2} \times (7) (7) + \int_{7}^{8} (8 y - y^{2}) d y \\ = \frac{49}{2} + {[\frac{8 y^{2}}{2} - \frac{y^{3}}{3}]}_{7}^{8} \\ = 24 \frac{1}{2} + [4 {(8)}^{2} - \frac{{(8)}^{3}}{3}] - [4 {(7)}^{2} - \frac{{(7)}^{3}}{3}] \\ = 24 \frac{1}{2} + 85 \frac{1}{3} - 81 \frac{2}{3} \\ = 28 \frac{1}{6} {unit}^{2} \end{array}