8.2c Probability of an Event

Posted on May 21, 2020 by Myhometuition

8.2c Probability of an Event

Example:

The masses of pears in a fruit stall are normally distributed with a mean of 220 g and a variance of 100 g. Find the probability that a pear that is picked at random has a mass

(a) of more than 230 g.

(b) between 210 g and 225 g.

Hence, find the value of h such that 90% of the pears weigh more than h g.

Solution:

µ = 220 g

σ = √100 = 10 g

Let X be the mass of a pear.

(a)

\begin{array}{l} P (X > 230) \\ = P (Z > \frac{230 - 220}{10}) \leftarrow \begin{array}{l} Convert to standard normal \\ distribution using Z = \frac{X - μ}{σ} \end{array} \\ = P (Z > 1) \\ = 0.1587 \end{array}

(b)

\begin{array}{l} P (210 < X < 225) \\ = P (\frac{210 - 220}{10} < Z < \frac{225 - 220}{10}) \leftarrow \begin{array}{l} Convert to standard normal \\ distribution using Z = \frac{X - μ}{σ} \end{array} \\ = P (- 1 < Z < 0.5) \\ = 1 - P (Z > 1) - P (Z > 0.5) \\ = 1 - 0.1587 - 0.3085 \\ = 0.5328 \end{array}

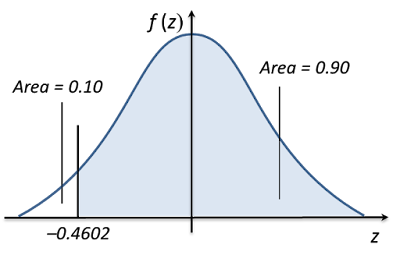
For 90% (probability = 0.9) of the pears weigh more than h g,

P (X > h) = 0.9

P (X < h) = 1 – 0.9

= 0.1

From the standard normal distribution table,

P (Z > 0.4602) = 0.1

P (Z < –0.4602) = 0.1

\begin{array}{l} \frac{h - 220}{10} = - 0.4602 \\ h - 220 = - 4.602 \\ h = 215.4 \end{array}