Home › SPM Add Maths › Trigonometry Functions › 5.5.1a Proving Trigonometric Identities Using Addition Formula And Double Angle Formulae (Part 2)

5.5.1a Proving Trigonometric Identities Using Addition Formula And Double Angle Formulae (Part 2)

Posted on by
Example 3:
(a) Given that sinP= 3 5  and sinQ= 5 13 ,  such that P is an acute angle and Q is an obtuse angle, without using tables or a calculator, find the value of cos (P + Q).

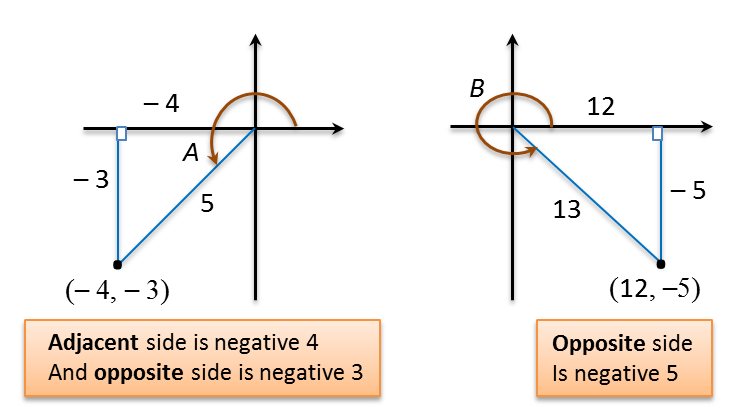
(b) Given that sinA=− 3 5  and sinB= 12 13 ,  such that A and B are angles in the third and fourth quadrants respectively, without using tables or a calculator, find the value of sin (A – B).

Solution:
(a)
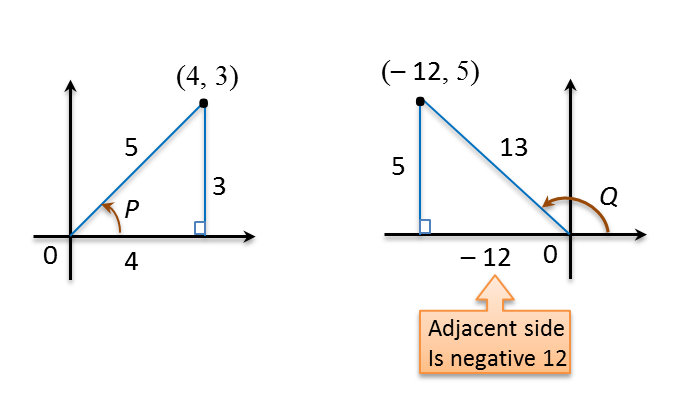sin P = 3 5 , cos P = 4 5 sin Q = 5 13 , cos Q = − 12 13 cos ( P + Q ) = cos A cos B − sin A sin B = ( 4 5 ) ( − 12 13 ) − ( 3 5 ) ( 5 13 ) = − 48 65 − 15 65 = − 63 65


(b)


sin A = − 3 5 , cos A = − 4 5 sin B = − 5 13 , cos B = 12 13 s i n ( A − B ) = s i n A cos B − c o s A sin B = ( − 3 5 ) ( 12 13 ) − ( − 4 5 ) ( − 5 13 ) = − 36 65 − 20 65 = − 56 65