6.6 Measures of Dispersion (Part 2)

Posted on May 26, 2020 by Myhometuition

(B) Medians and Quartiles

1. The first quartile (Q₁)is a number such that 1 4 of the total number of data that has a value less than the number.

2. The median is the second quartile which is the value that lies at the centre of the data.

3. The third quartile (Q₃) is a number such that 3 4of the total number of data that has a value less than the number.

4. The interquartile range is the difference between the third quartile and the first quartile.

Interquartile range = third quartile – first quartile

Example 2:

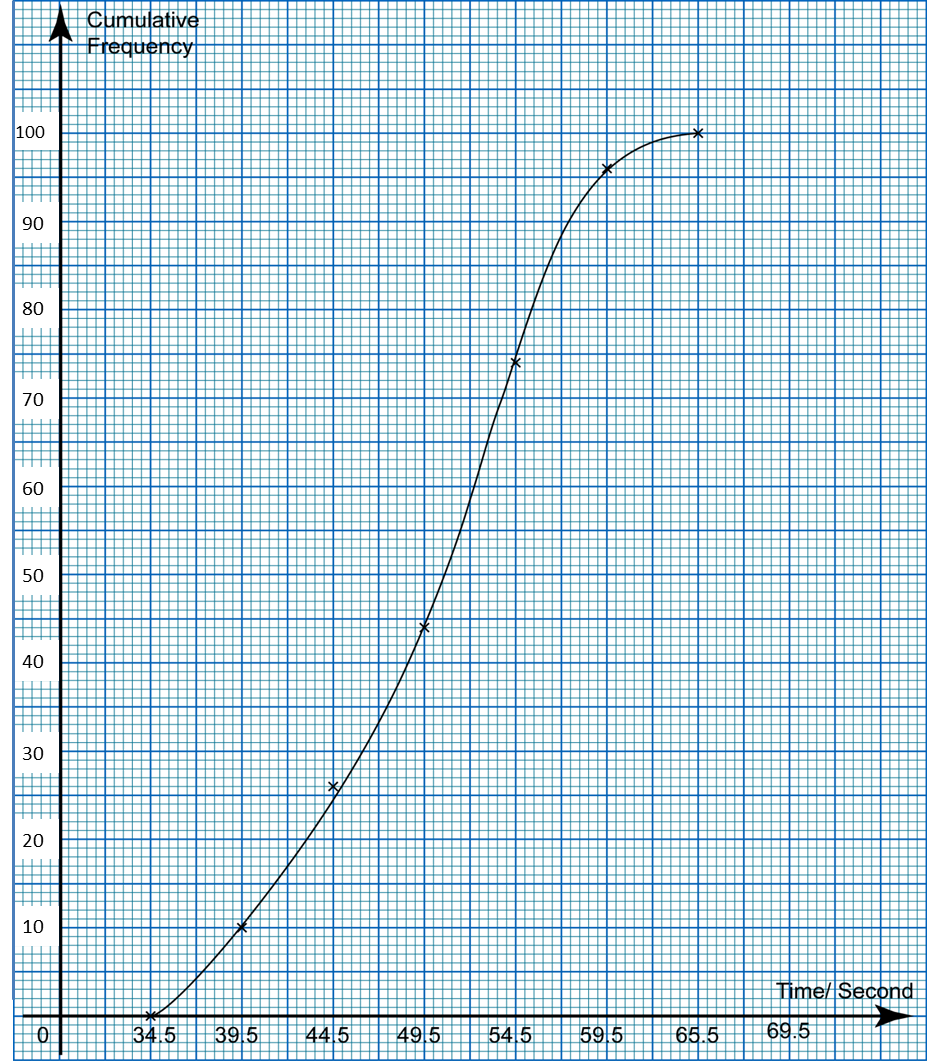
The ogive in the diagram shows the distribution of time (to the nearest second) taken by 100 students in a swimming competition. From the ogive, determine

(a) the median,

(b) the first quartile,

(c) the third quartile

(d) the interquartile range of the time taken.

Solution:

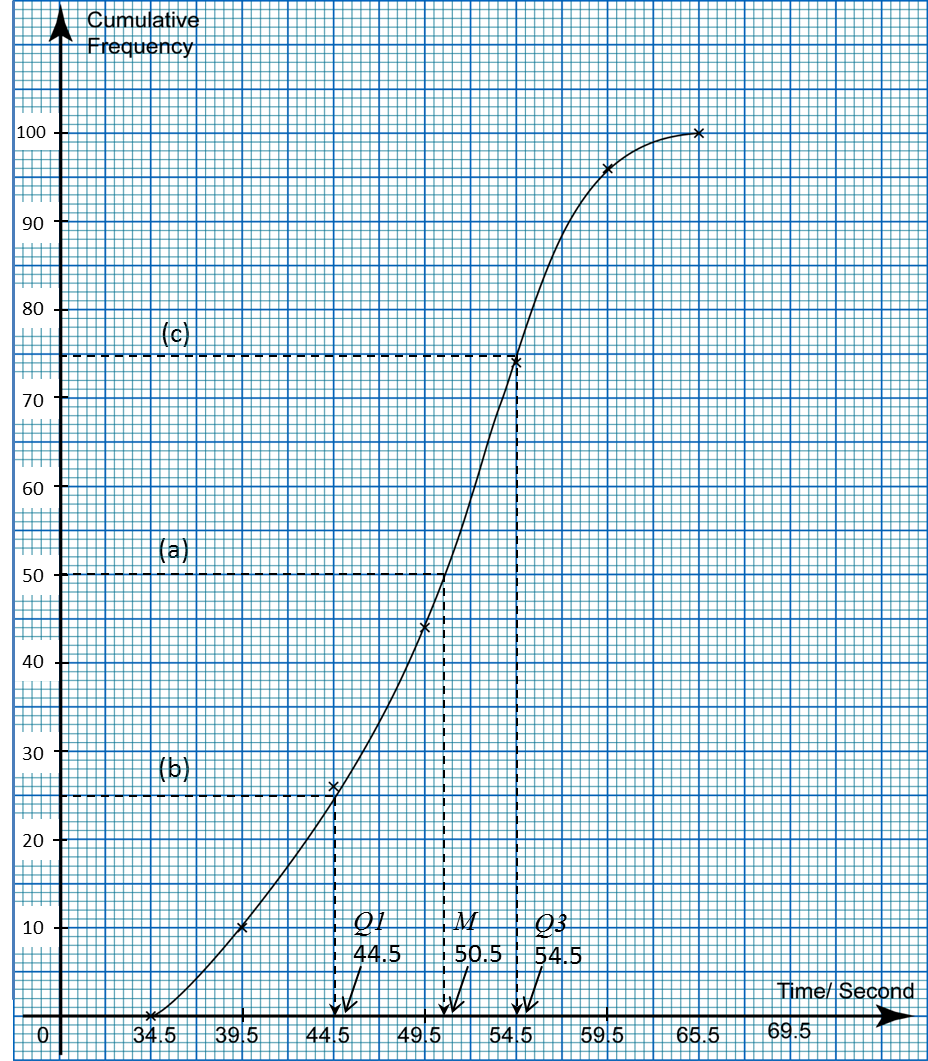
$\begin{array}{l} (a) \frac{1}{2} of 100 students = \frac{1}{2} \times 100 = 50 \\ From the ogive, median, M = 50.5 second \\ (b) \frac{1}{4} of 100 students = \frac{1}{4} \times 100 = 25 \\ From the ogive, first quartile, Q_{1} = 44.5 second \\ (c) \frac{3}{4} of 100 students = \frac{3}{4} \times 100 = 75 \\ From the ogive, third quartile, Q_{3} = 5 4.5 second \end{array}$

(d)

Interquartile range

= Third quartile – First quartile

= 54.5 – 44.5

= 10.0 second