8.2 Angle between Tangent and Chord (Example 1 & 2)

Example 1:

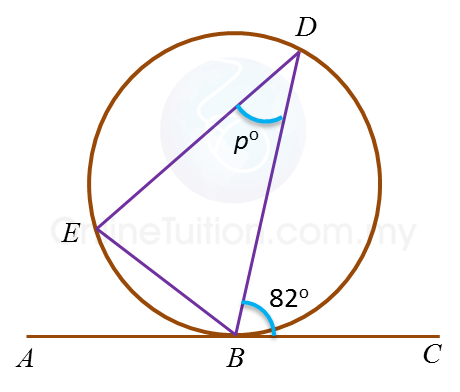
In the diagram, ABC is a tangent to the circle BDE at B.

The length of arc BD is equal to the length of arc DE.

Find the value of p.

Solution:

Angle BED = 82^o ← (angle in alternate segment)

Angle DBE = 82^o ← (Arc BD = Arc DE, BDE is an isosceles triangle)

Therefore p= 180^o – 82^o – 82^o= 16^o

Example 2:

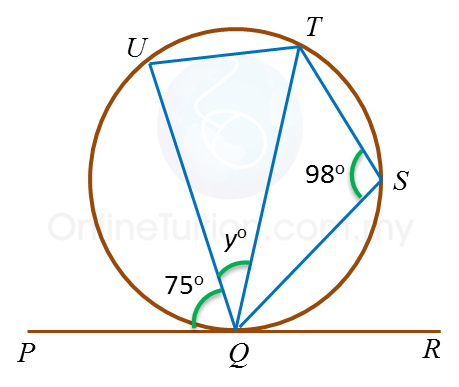
In the diagram, PQR is a tangent to the circle QSTU at Q.

Find the value of y.

Solution:

Angle QUT

= 180^o– 98^o ← (opposite angle in cyclic quadrilateral QSTU )

= 82^o

Angle QTU = 75^o ← (angle in alternate segment)

Therefore y= 180^o – (82^o + 75^o) ← (Sum of interior angles in ∆ QTU)

= 23^o