9.6 SPM Practice (Long Questions)

Question 3:
Diagram below shows the locations of points A (34^o S, 40^o W) and B (34^o S, 80^o E) which lie on the surface of the earth. AC is a diameter of the common parallel of latitude 34^o S.


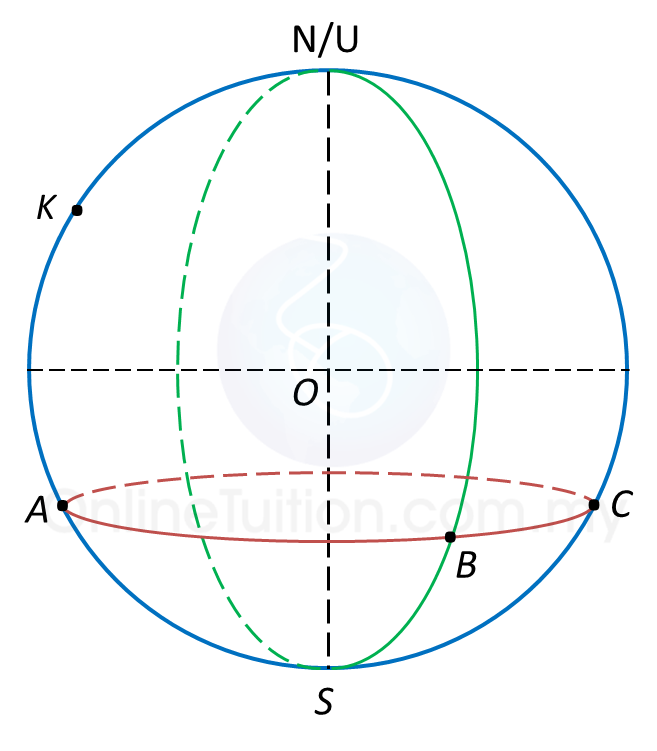
(a) State the longitude of C.

(b) Calculate the distance, in nautical mile, from A due east to B, measured along the common parallel of latitude 34^o S.

(c) K lies due north of A and the shortest distance from A to K measured along the surface of the earth is 4440 nautical miles.
Calculate the latitude of K.

(d) An aeroplane took off from B and flew due west to A along the common parallel of latitude. Then, it flew due north to K. The average speed for the whole flight was 450 knots.
Calculate the total time, in hours, taken for the whole flight.

Solution:
(a)
Longitude of C = (180^o – 40^o) E = 140^o E

(b)
Distance of AB
= (40 + 80) x 60 x cos 34^o
= 120 x 60 x cos 34^o
= 5969 nautical miles

(c)
$\begin{array}{l}\angle AOK=\frac{4440}{60}\\ ={74}^o\\ \text{Latitude of }K={\left(74-34\right)}^{o}N\\ ={40}^{o}N\end{array}$

(d)
$\begin{array}{l}\text{Total distance travelled}\\ BA+AK\\ =5969+4440\\ =10409\text{ nautical miles}\\ \\ \text{Total time taken =}\frac{\text{Total distance travelled}}{\text{Average speed}}\\ =\frac{10409}{450}\\ =23.13\text{ hours}\end{array}$