6.7 SPM Practice (Long Questions)

Posted on May 30, 2020 by Myhometuition

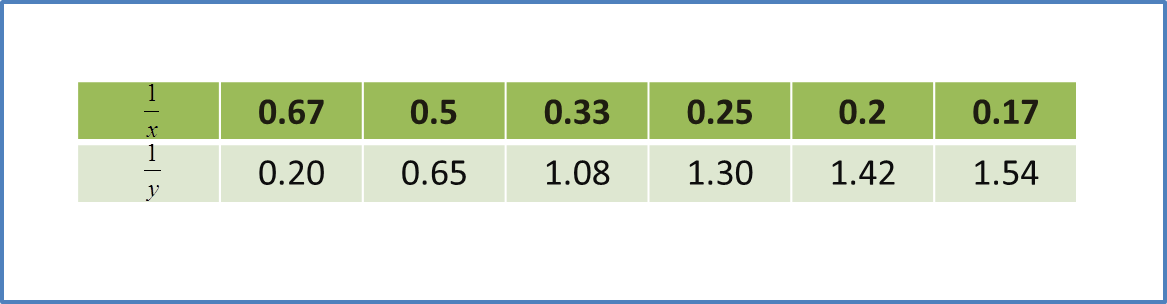
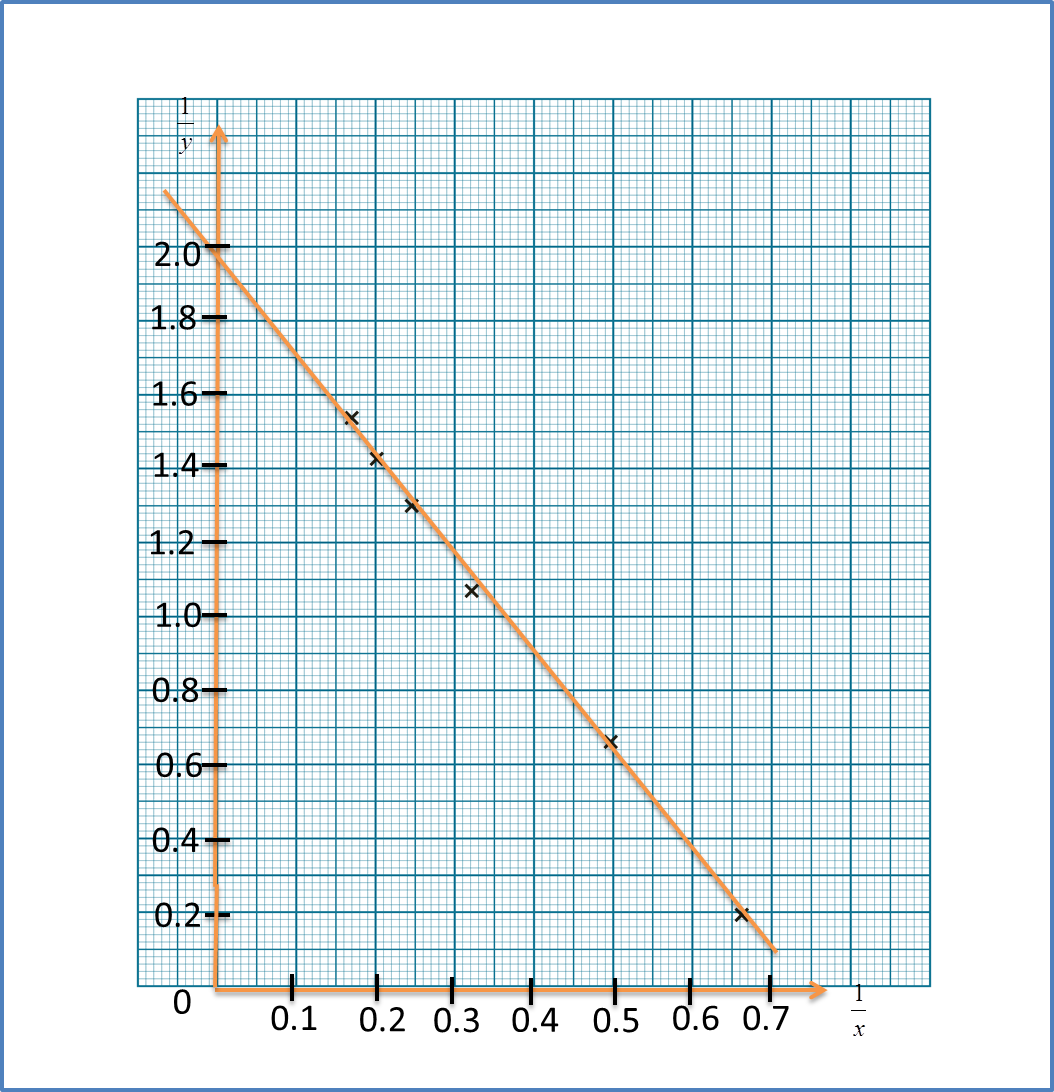
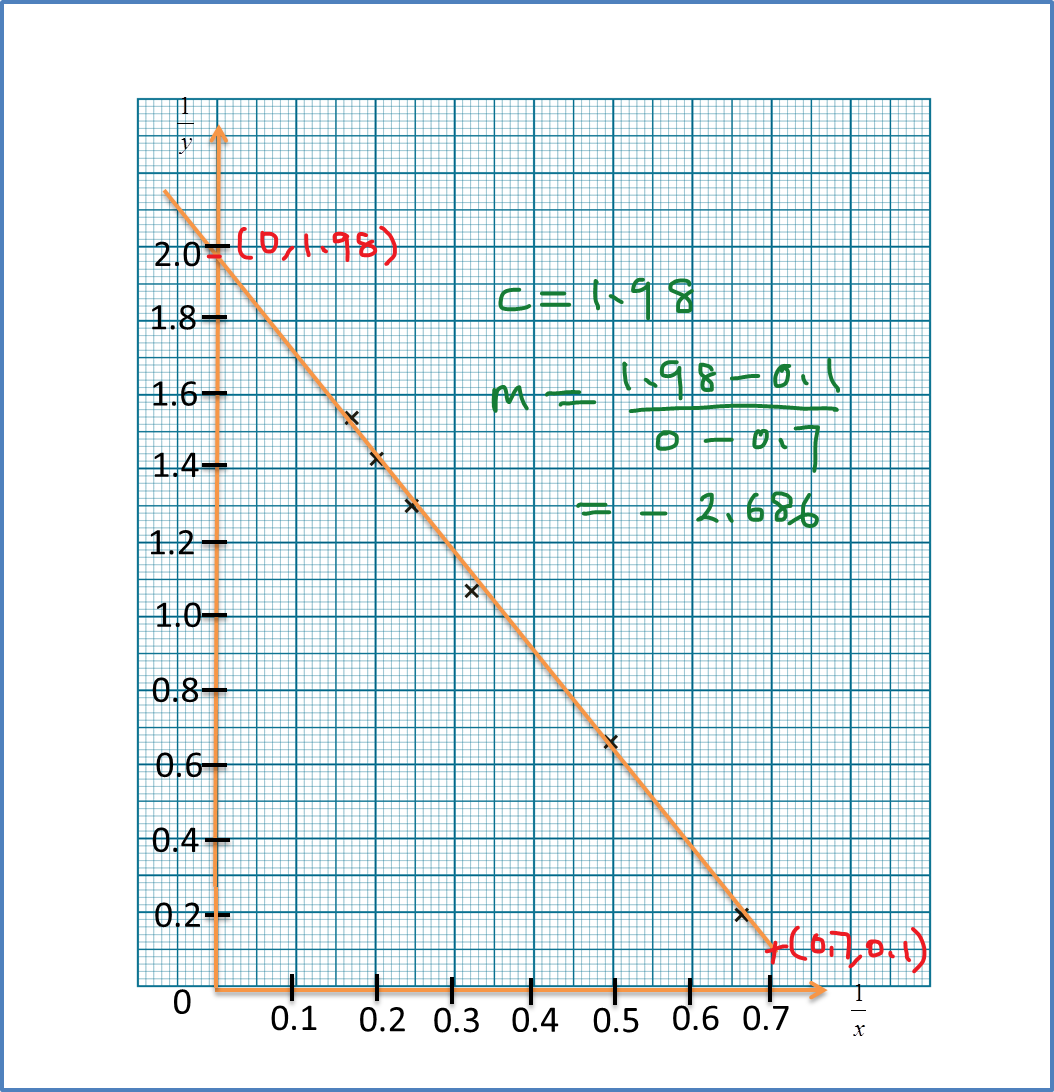
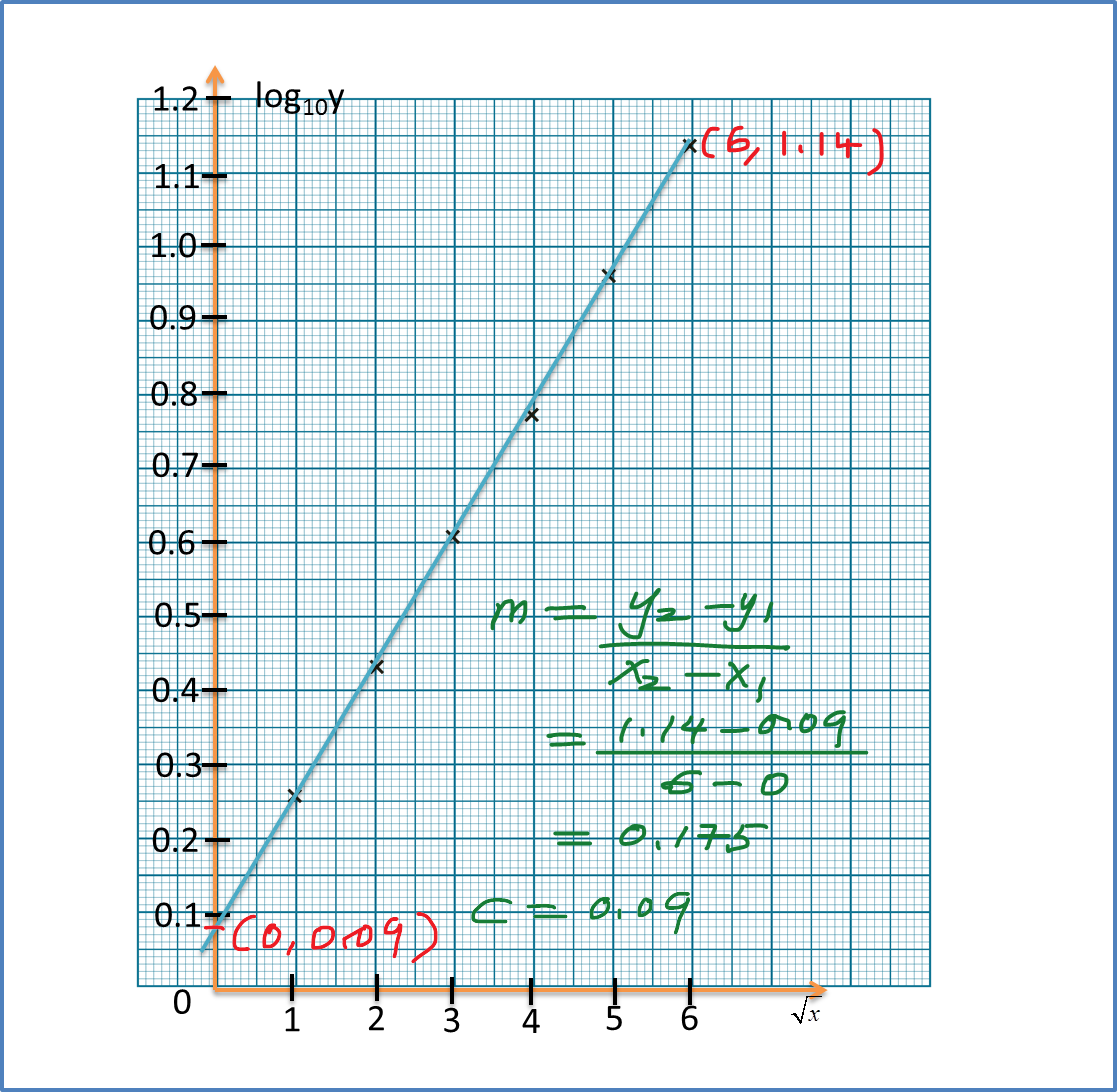
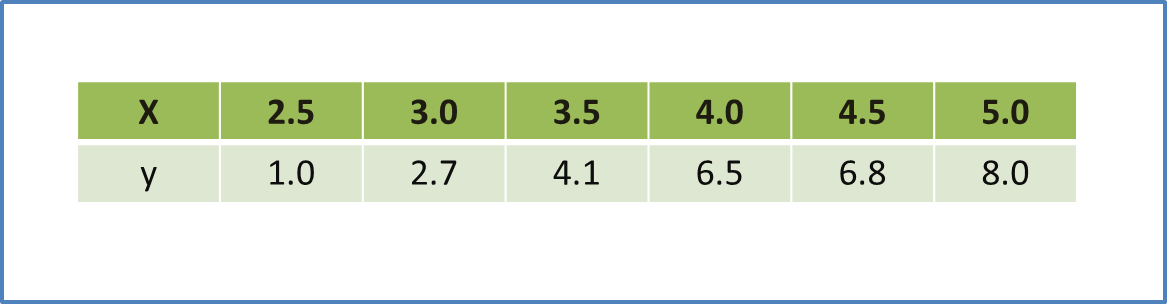
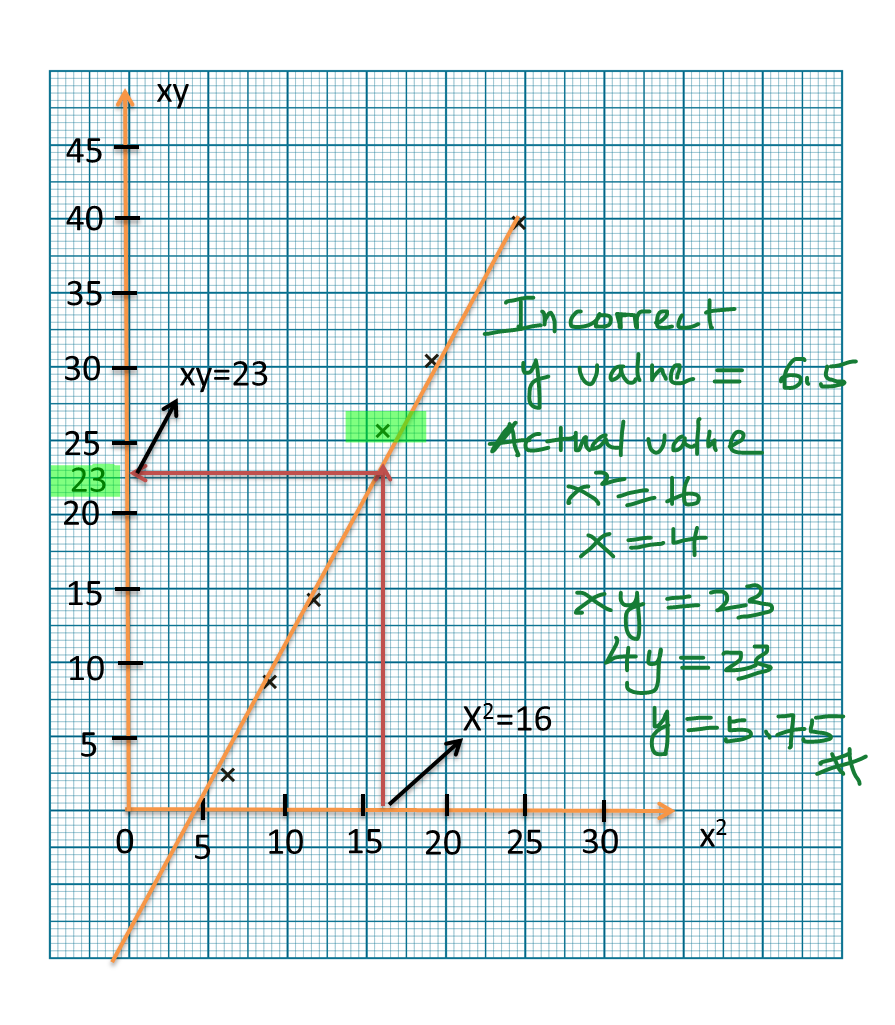
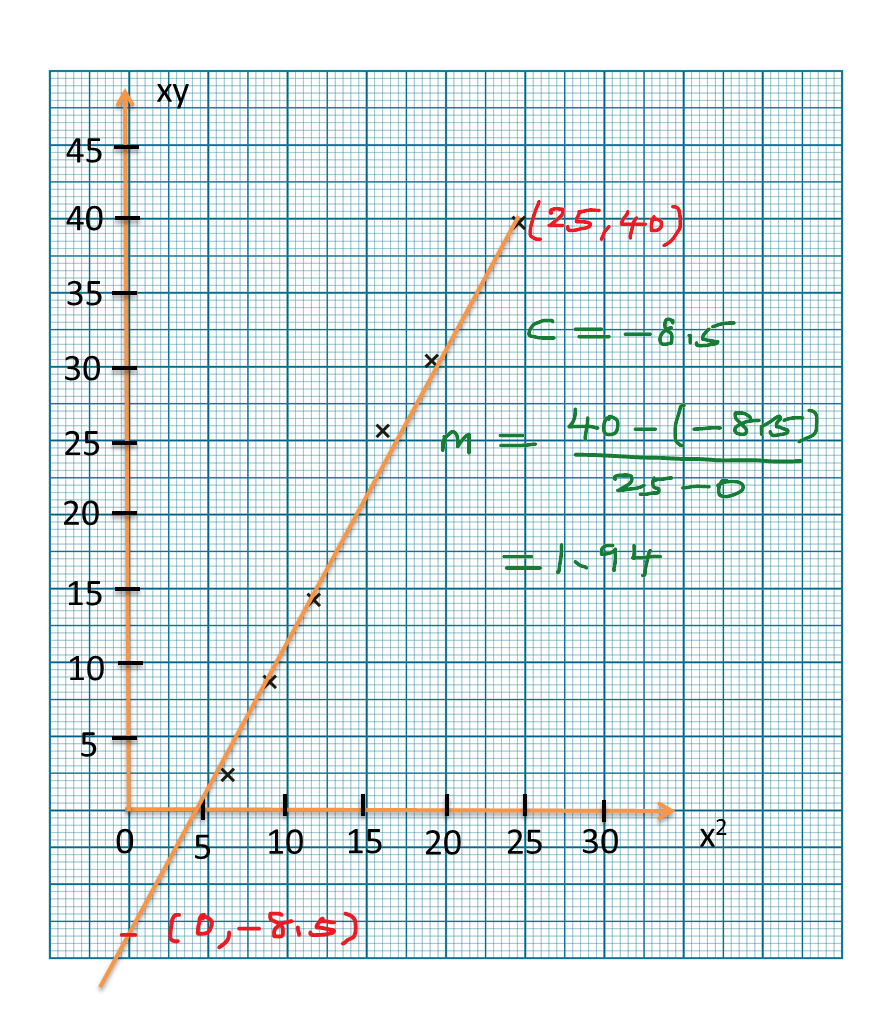
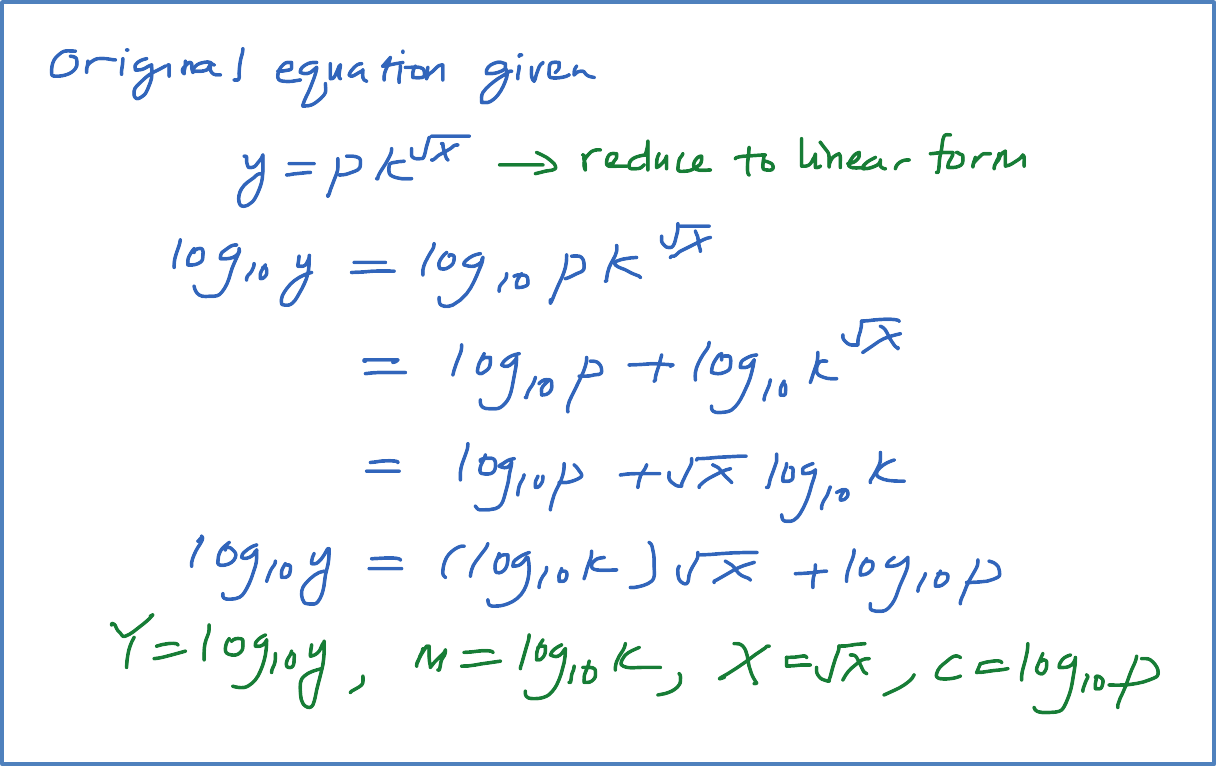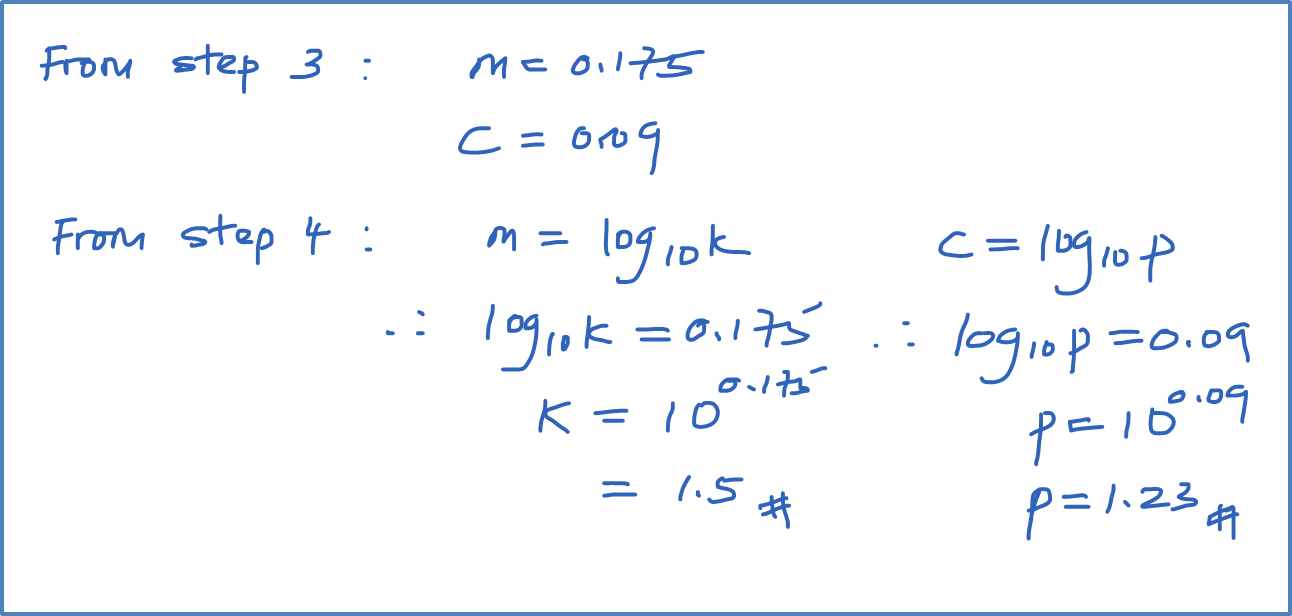Question 9 (12 marks):
The data in the Diagram shows the mass, in g, of 30 strawberries plucked by a tourist from a farm.

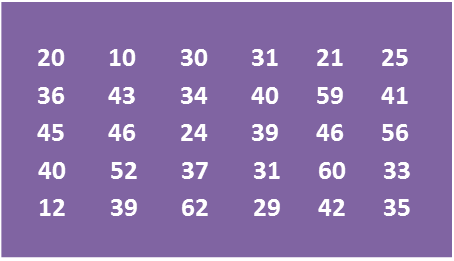Diagram

(a) Based on the Diagram, complete Table 3 in the answer space.

(b) Based on Table, calculate the estimated mean mass of a strawberry.

(c) For this part of the question, use graph paper.
By using the scale of 2 cm to 10 g on the horizontal axis and 2 cm to 1 strawberry on the vertical axis, draw a histogram for the data.

(d) Based on the histogram drawn in 14(c), state the number of strawberries with the mass of more than 50 g.

Answer:

Solution:
(a)

(b)

\begin{array}{l} Estimated mean mass \\ = \frac{Total [midpoint \times frequency]}{Total frequencies} \\ = \frac{\begin{array}{l} 2 (14.5) + 5 (24.5) + 10 (34.5) + 8 (44.5) + \\ 3 (54.5) + 2 (64.5) \end{array}}{2 + 5 + 10 + 8 + 3 + 2} \\ = \frac{1145}{30} \\ = 38.17 \end{array}

(c)

(d)
Number of strawberries with the mass more than 50 g
= 3 + 2
= 5

6.7 SPM Practice (Long Questions)

Posted on May 30, 2020 by Myhometuition

Question 8 (12 marks):
Diagram shows the marks obtained by a group of 36 students in a Mathematics test.

Diagram

(a) Based on the data in Diagram, complete Table in the answer space.

(b) Based on the Table, calculate the estimated mean mark of a student.

(c) For this part of the question, use graph paper.
By using the scale of 2 cm to 5 marks on the horizontal axis and 2 cm to 1 student on the vertical axis, draw a frequency polygon for the data.

(d) Based on the frequency polygon in 8(c), state the number of students who obtained more than 40 marks.

Answer:

Table

Solution:
(a)

(b)

\begin{array}{l} Estimated mean mark \\ = \frac{Total [Frequency \times midpoint]}{Total frequency} \\ = \frac{\begin{array}{l} 2 (28) + 5 (33) + 7 (38) + 10 (43) + \\ 8 (48) + 4 (53) \end{array}}{2 + 5 + 7 + 10 + 8 + 4} \\ = \frac{1513}{36} \\ = 42.03 \end{array}

(c)

(d)
Number of students who obtained more than 40 marks
= 10 + 8 + 4
= 22 students

SPM Practice Question 2

Posted on May 30, 2020 by Myhometuition

Question 2:
The third term and the sixth term of a geometric progression are 24 and

7 \frac{1}{9}

respectively. Find
(a) the first term and the common ratio,
(b) the sum of the first five terms,
(c) the sum of the first n terms with n is very big approaching rⁿ ≈ 0.

Solution:
(a)

\begin{array}{l} Given T_{3} = 24 \\ a r^{2} = 24 ........... (1) \\ Given T_{6} = 7 \frac{1}{9} \\ a r^{5} = \frac{64}{9} ........... (2) \\ \frac{(2)}{(1)} : \frac{a r^{5}}{a r^{2}} = \frac{\frac{64}{9}}{24} \\ r^{3} = \frac{8}{27} \\ r = \frac{2}{3} \end{array}

\begin{array}{l} Substitute r = \frac{2}{3} into (1) \\ a {(\frac{2}{3})}^{2} = 24 \\ a (\frac{4}{9}) = 24 \\ a = 24 \times \frac{9}{4} \\ = 54 \\ ∴ the first term 54 and the common ratio is \frac{2}{3} . \end{array}

(b)

\begin{array}{l} S_{5} = \frac{54 [1 - {(\frac{2}{3})}^{5}]}{1 - \frac{2}{3}} \\ = 54 \times \frac{211}{243} \times \frac{3}{1} \\ = 140 \frac{2}{3} \\ ∴ sum of the first five term is 140 \frac{2}{3} . \end{array}

(c)

\begin{array}{l} When - 1 < r < 1 and n becomes \\ very big approaching r^{n} \approx 0, \\ ∴ S_{n} = \frac{a}{1 - r} \\ = \frac{54}{1 - \frac{2}{3}} \\ = 162 \end{array}

Therefore, sum of the first n terms with n is very big approaching rⁿ ≈ 0 is 162.

Short Questions (Question 7 & 8)

Posted on May 30, 2020 by Myhometuition

Question 7:

The masses of mangoes in a stall have a normal distribution with a mean of 200 g and a standard deviation of 30 g.

(a) Find the mass, in g, of a mango whose z-score is 0.5.

(b) If a mango is chosen at random, find the probability that the mango has a mass of at least 194 g.

Solution:

µ = 200 g

σ = 30 g

Let X be the mass of a mango.

(a)

\begin{array}{l} \frac{X - 200}{30} = 0.5 \\ X = 0.5 (30) + 200 \\ X = 215 g \end{array}

(b)

\begin{array}{l} P (X \geq 194) \\ = P (Z \geq \frac{194 - 200}{30}) \\ = P (Z \geq - 0.2) \\ = 1 - P (Z > 0.2) \\ = 1 - 0.4207 \\ = 0.5793 \end{array}

Question 8:

Diagram below shows a standard normal distribution graph.

The probability represented by the area of the shaded region is 0.3238.

(a) Find the value of k.

(b) X is a continuous random variable which is normally distributed with a mean of 80 and variance of 9.

Find the value of X when the z-score is k.

Solution:

(a)

P(Z > k) = 0.5 – 0.3238

= 0.1762

k = 0.93

(b)

µ = 80,

σ² = 9, σ = 3

\begin{array}{l} \frac{X - 80}{3} = 0.93 \\ X = 3 (0.93) + 80 \\ X = 82.79 \end{array}

Short Questions (Question 5 & 6)

Posted on May 30, 2020 by Myhometuition

Question 5:

Diagram below shows the graph of a binomial distribution of X.

(a) the value of h,

(b) P (X ≥ 3)

Solution:

(a)

P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) + P (X = 4) = 1

\begin{array}{l} \frac{1}{16} + \frac{1}{4} + h + \frac{1}{4} + \frac{1}{16} = 1 \\ h = 1 - \frac{5}{8} \\ h = \frac{3}{8} \end{array}

(b)

P (X ≥ 3) = P (X = 3) + P (X = 4)

P (X \geq 3) = \frac{1}{4} + \frac{1}{16} = \frac{5}{16}

Question 6:

The random variable X represents a binomial distribution with 10 trails and the probability of success is ¼.

(a) the standard deviation of the distribution,

(b) the probability that at least one trial is success.

Solution:

(a)

n = 10, p = ¼

\begin{array}{l} Standard deviation = \sqrt{n p q} \\ = \sqrt{10 \times \frac{1}{4} \times \frac{3}{4}} \\ = 1.875 \end{array}

(b)

\begin{array}{l} P (X = r) = C_{r} {(\frac{1}{4})}^{r} {(\frac{3}{4})}^{10 - r} \\ P (X \geq 1) \\ = 1 - P (X < 1) \\ = 1 - P (X = 0) \\ = 1 - C_{0} {(\frac{1}{4})}^{0} {(\frac{3}{4})}^{10} \\ = 0.9437 \end{array}

SPM Practice 2 (Question 11 & 12)

Posted on May 30, 2020 by Myhometuition

Question 11 (3 marks):
Diagram 6 shows the graph of a straight line

\frac{x^{2}}{y} against \frac{1}{x} .

Diagram 11

Based on Diagram 6, express y in terms of x.

Solution:

\begin{array}{l} m = \frac{4 - (- 5)}{6 - 0} = \frac{3}{2} \\ c = - 5 \\ Y = \frac{x^{2}}{y}, X = \frac{1}{x} \\ Y = m X + c \\ \frac{x^{2}}{y} = \frac{3}{2} (\frac{1}{x}) + (- 5) \\ \frac{x^{2}}{y} = \frac{3}{2 x} - 5 \\ \frac{x^{2}}{y} = \frac{3 - 10 x}{2 x} \\ \frac{y}{x^{2}} = \frac{2 x}{3 - 10 x} \\ y = \frac{2 x^{3}}{3 - 10 x} \end{array}

Question 12 (3 marks):
The variables x and y are related by the equation

y = x + \frac{r}{x^{2}}

, where r is a constant. Diagram 8 shows a straight line graph obtained by plotting

(y - x) against \frac{1}{x^{2}} .

Diagram 12

Express h in terms of p and r.

Solution:

\begin{array}{l} y = x + \frac{r}{x^{2}} \\ y - x = r (\frac{1}{x^{2}}) + 0 \\ Y = m X + c \\ m = r, c = 0 \\ m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ r = \frac{5 p - 0}{\frac{h}{2} - 0} \\ \frac{h r}{2} = 5 p \\ h r = 10 p \\ h = \frac{10 p}{r} \end{array}

SPM Practice 2 (Linear Law) – Question 1

Posted on May 30, 2020 by Myhometuition

Question 1 (10 marks):
Use a graph to answer this question.
Table 1 shows the values of two variables, x and y, obtained from an experiment. A straight line will be obtained when a graph of

\frac{y^{2}}{x} against \frac{1}{x}

is plotted.

(a) Based on Table 1, construct a table for the values of

\frac{1}{x} and \frac{y^{2}}{x} .

\begin{array}{l} (b) Plot \frac{y^{2}}{x} against \frac{1}{x}, using a scale of 2 cm to 0 .1 unit on the \frac{1}{x} -axis \\ and 2cm to 2 units on the \frac{y^{2}}{x} -axis . \\ Hence, draw the line of best fit . \end{array}

(c) Using the graph in 1(b)
(i) find the value of y when x = 2.7,
(ii) express y in terms of x.

Solution:
(a)

(b)

(c)(i)

\begin{array}{l} When x = 2.7, \frac{1}{x} = 0.37 \\ From graph, \\ \frac{y^{2}}{x} = 5.2 \\ \frac{y^{2}}{2.7} = 5.2 \\ y = 3.75 \end{array}

(c)(ii)

\begin{array}{l} Form graph, y -intercept, c = –4 \\ gradient, m = \frac{16 - (- 4)}{0.8 - 0} = 25 \\ Y = m X + c \\ \frac{y^{2}}{x} = 25 (\frac{1}{x}) - 4 \\ y = \sqrt{25 - 4 x} \end{array}

SPM Practice 3 (Linear Law) – Question 6

Posted on May 30, 2020 by Myhometuition

Question 6
The table below shows the values of two variables, x and y, obtained from an experiment. The variables x and y are related by the equation

\frac{a}{y} = \frac{b}{x} + 1

, where k and p are constants.

(a) Based on the table above, construct a table for the values of

\frac{1}{x}

and

\frac{1}{y}

. Plot

\frac{1}{y}

against

\frac{1}{x}

, using a scale of 2 cm to 0.1 unit on the

\frac{1}{x}

- axis and 2 cm to 0.2 unit on the

\frac{1}{y}

- axis. Hence, draw the line of best fit.
(b) Use the graph from (b) to find the value of
(i) a,
(ii) b.

Solution
Step 1 : Construct a table consisting X and Y.

Step 2 : Plot a graph of Y against X, using the scale given and draw a line of best fit

Steps to draw line of best fit - Click here

Step 3 : Calculate the gradient, m, and the Y-intercept, c, from the graph

Step 4 : Rewrite the original equation given and reduce it to linear form

Step 5 : Compare with the values of m and c obtained, find the values of the unknown required

SPM Practice 3 (Linear Law) – Question 5

Posted on May 30, 2020 by Myhometuition

Question 5
The following table shows the corresponding values of two variables, x and y, that are related by the equation

y = p k^{\sqrt{x}}

, where p and k are constants.

(a) Plot

\log_{10} y

against

\sqrt{x}

. Hence, draw the line of best fit

(b) Use your graph in (a) to find the values of p and k.

Solution
Step 1 : Construct a table consisting X and Y.

Step 2 : Plot a graph of Y against X, using the scale given and draw a line of best fit

For steps to draw line of best fit - Click here

Step 3 : Calculate the gradient, m, and the Y-intercept, c, from the graph

Step 4 : Rewrite the original equation given and reduce it to linear form

Step 5 : Compare with the values of m and c obtained, find the values of the unknown required

SPM Practice 2 (Linear Law) – Question 4

Posted on May 30, 2020 by Myhometuition

Question 4
The table below shows the corresponding values of two variables, x and y, that are related by the equation

y = q x + \frac{p}{q x}

, where p and q are constants.

One of the values of y is incorrectly recorded.
(a) Using scale of 2 cm to 5 units on the both axis, plot the graph of xy against

x^{2}

. Hence, draw the line of best fit

(b) Use your graph in (a) to answer the following questions:
(i) State the values of y which is incorrectly recorded and determine its actual value.
(ii) Find the value of p and of q.

Solution
Step 1 : Construct a table consisting X and Y.

Step 2 : Plot a graph of Y against X, using the scale given and draw a line of best fit

Steps to draw line of best fit - Click here

(b) (i) State the values of y which is incorrectly recorded and determine its actual value.

Step 3 : Calculate the gradient, m, and the Y-intercept, c, from the graph

Step 4 : Rewrite the original equation given and reduce it to linear form

Step 5 : Compare with the values of m and c obtained, find the values of the unknown required