Question 3
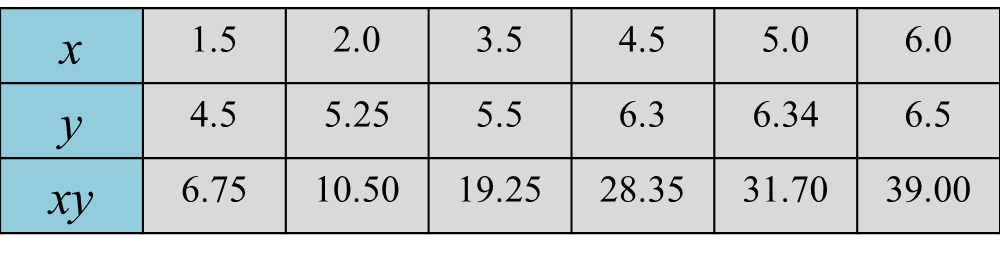
The table below shows the corresponding values of two variables,
x and
y, that are related by the equation
, where h and k are constants.
(a)
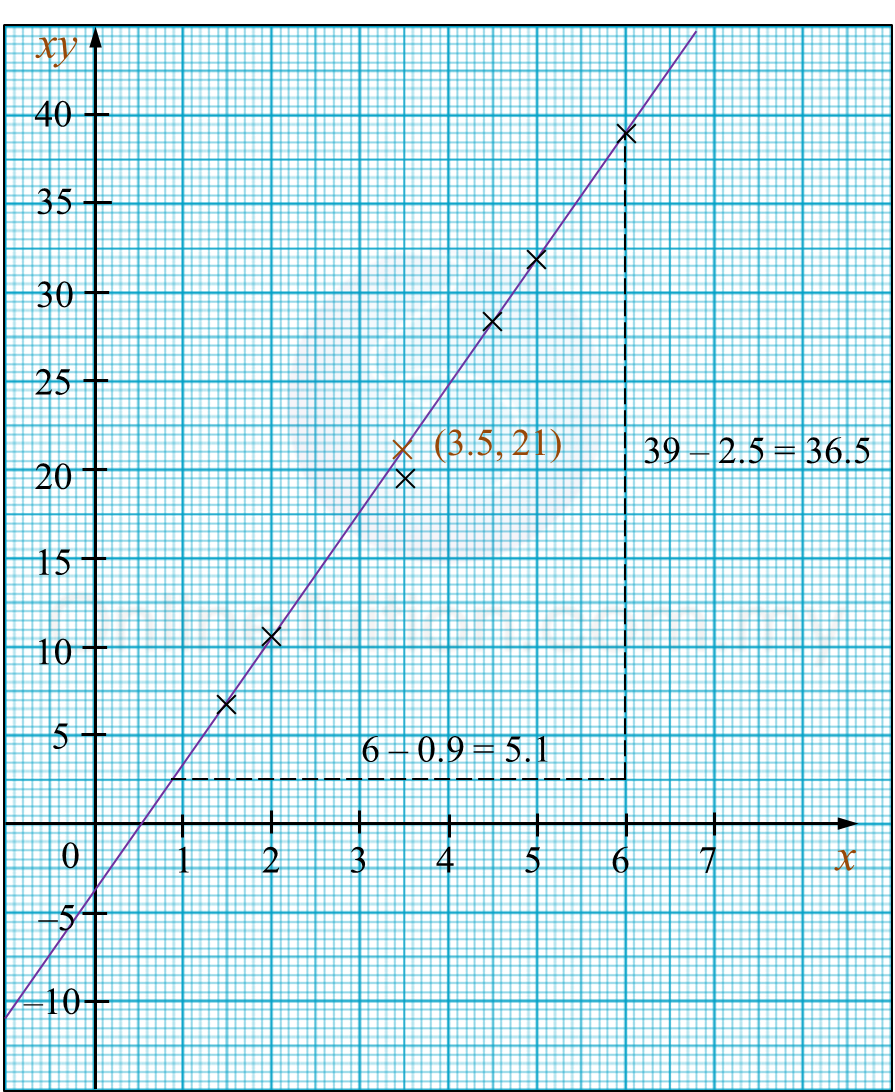
Using a scale of 2 cm to 1 unit on the
x - axis and 2 cm to 0.2 units on the
– axis, plot the graph of
against x . Hence, draw the line of best fit.
(b)
Use your graph in (a) to find the values of
(i)
h,
(ii)
k,
(iii)
y when
x = 6.
Solution
Step 1 : Construct a table consisting
X and
Y.
Step 2 : Plot a graph of Y against X, using the scale given and draw a line of best fit
Steps to draw line of best fit - Click here
Step 3 : Calculate the gradient, m, and the Y-intercept, c, from the graph
Step 4 : Rewrite the original equation given and reduce it to linear form
Step 5 : Compare with the values of
m and
c obtained, find the values of the unknown required
(b) (iii) find the value of y when x = 6.


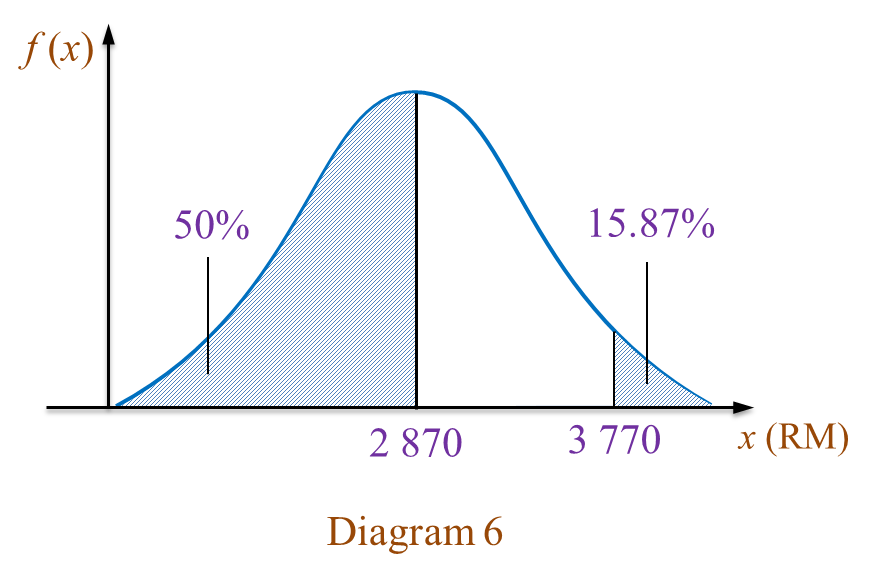 (a)(i) Find the standard deviation.
(a)(i) Find the standard deviation.