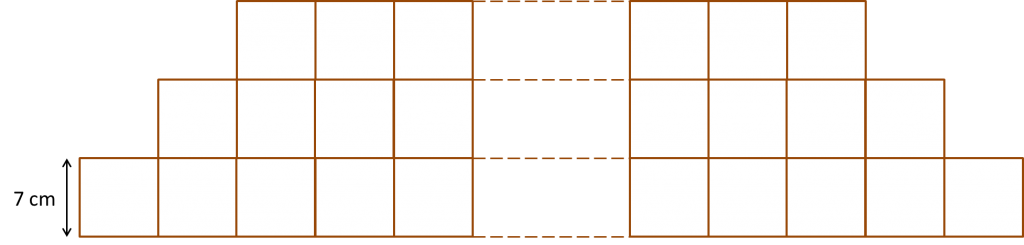
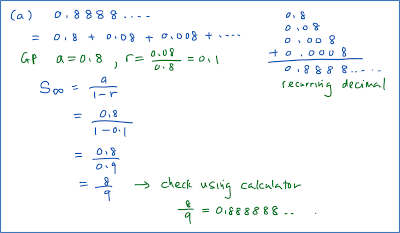
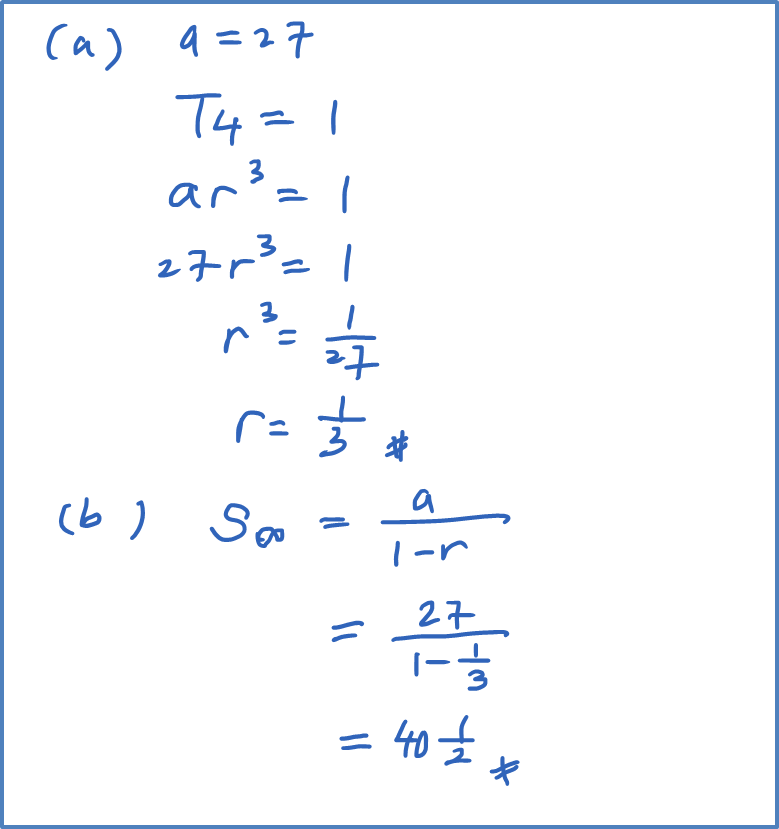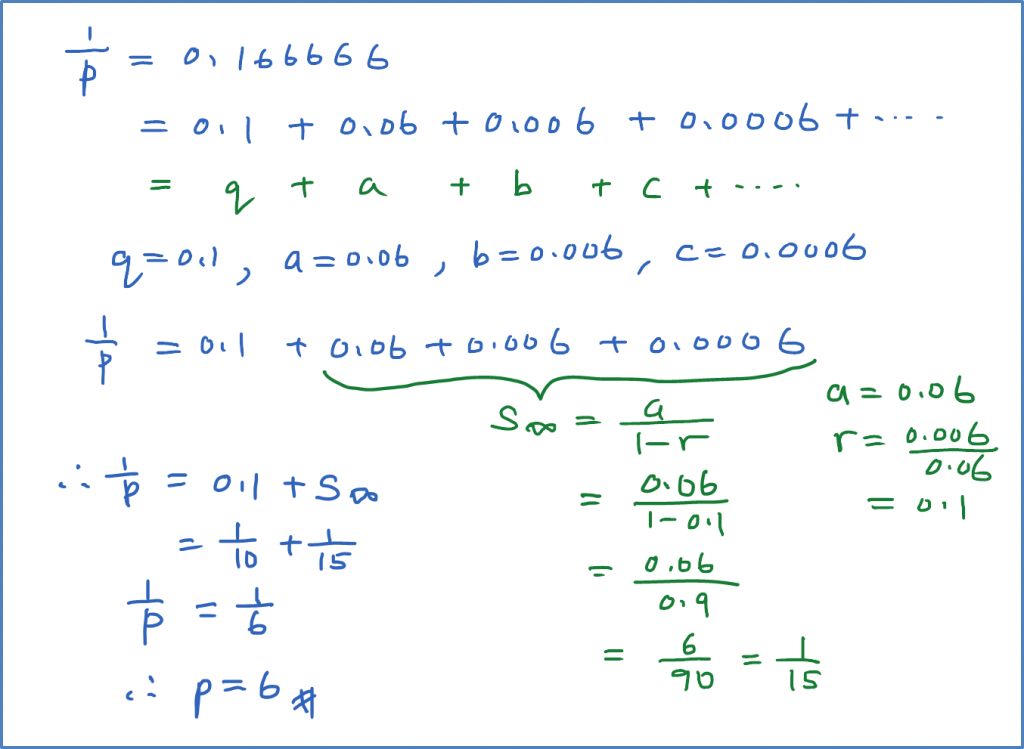Tn = a + (n − 1) d where a = first term d = common difference n = the number of term Tn  = the nth term

If a, b, c are three consecutive terms of an arithmetic progression, then c – b = b – a

$\begin{array}{l}x=\frac{1}{3}\\ \frac{1}{3}+1,\text{2}\left(\frac{1}{3}\right)+3,6\\ \frac{\text{4}}{\text{3}}\text{, 3}\frac{2}{3}\text{, 6}\\ d=\text{3}\frac{2}{3}-\frac{\text{4}}{\text{3}}=2\frac{1}{3}\end{array}$

Solution:

$\begin{array}{l}{T}_n=a{r}^{n-1}\\ T_1=a{r}^{1-1}=a{r}^0=a\leftarrow (\text{First term})\\ T_2=a{r}^{2-1}=a{r}^1=ar\leftarrow (Second\text{term})\\ T_3=a{r}^{3-1}=a{r}^2\leftarrow (Third\text{term})\\ T_4=a{r}^{4-1}=a{r}^3\leftarrow (\text{Fourth term})\end{array}$

(a)
$\begin{array}{l}8,4,2,\mathrm{.....}\\ a=8,r=\frac{4}{8}=\frac{1}{2}\\ T_8=a{r}^7\\ T_8=8{\left(\frac{1}{2}\right)}^7=\frac{1}{16}\end{array}$

(b)
$\begin{array}{l}\frac{16}{27},\frac{8}{9},\frac{4}{3},\mathrm{.....}\\ a=\frac{16}{27}\\ r=\frac{T_2}{T_1}=\frac{\frac{16}{27}}{\frac{8}{9}}=\frac{2}{3}\\ T_6=a{r}^5\\ =\frac{16}{27}{\left(\frac{2}{3}\right)}^5=\frac{512}{6561}\end{array}$

(a)
$\begin{array}{l}-11,-8,-5,\mathrm{.....}\text{Find}{S}_{15}\\ a=-11,\\ d=-8-\left(-11\right)=3\\ S_{15}=\frac{15}{2}\left[2a+14d\right]\\ S_{15}=\frac{15}{2}\left[2\left(-11\right)+14\left(3\right)\right]=150\end{array}$

(b)
$\begin{array}{l}8,10\frac{1}{2},13,\mathrm{.....}\text{Find}{S}_{13}\\ a=8\\ d=10\frac{1}{2}-8=\frac{5}{2}\\ S_{13}=\frac{13}{2}\left[2a+12d\right]\\ S_{13}=\frac{13}{2}\left[2\left(8\right)+12\left(\frac{5}{2}\right)\right]=299\end{array}$

(c)
$\begin{array}{l}5,7,9,\mathrm{.....},75\leftarrow \left(\text{The last term}l=75\right)\\ a=5\\ d=7-5=2\\ S_n=\frac{n}{2}\left(a+l\right)\\ S_{36}=\frac{36}{2}\left(5+75\right)=1440\\ \\ \text{The last term}l=75\\ T_n=75\\ a+\left(n-1\right)d=75\\ 5+\left(n-1\right)\left(2\right)=75\\ \left(n-1\right)\left(2\right)=70\\ n-1=35\\ n=36\end{array}$

Question 1:
The fourth term of a geometric progression is –20. The sum of the fourth and the fifth term is –16. Find the first term and the common ratio of the progression.

Solution:

Question 2:
The fourth and the seventh terms of a geometric progression are 18 and 486 respectively. Find the third term.

Solution:

Question 3:
For a geometric progression, the sum of the first two terms is 30 and the third term exceeds the first term by 15. Find the common ratio and the first term of the geometry progression.

Solution:
$\begin{array}{l}{T}_1+T_2=30\\ a+ar=30\\ a\left(1+r\right)=30---(1)\\ T_3-T_1=15\\ a{r}^2-a=15\\ a\left(r^2-1\right)=15---(2)\\ \\ \frac{\left(2\right)}{\left(1\right)}=\frac{a\left(r^2-1\right)}{a\left(1+r\right)}=\frac{15}{30}\\ \frac{\left(r-1\right)\left(r+1\right)}{1+r}=\frac{1}{2}\to \boxed{\begin{array}{l}\left(r^2-1\right)=\\ \left(r-1\right)\left(r+1\right)\end{array}}\\ r-1=\frac{1}{2}\\ r=\frac{1}{2}+1=\frac{3}{2}\\ \\ \text{From (1),}\\ a\left(1+r\right)=30\\ a\left(1+\frac{3}{2}\right)=30\\ \frac{5a}{2}=30\\ a=12\end{array}$

Smart TIPS: Solving the simultaneous equation of a and r. Using the formula T _n = a r ⁿ⁻¹

Solution:
$\begin{array}{l}{T}_6=32\\ a{r}^5=32\text{ ----- (1)}\\ T_3=4\\ a{r}^2=4\text{ ----- (2)}\\ \frac{(1)}{(2)}=\frac{a{r}^5}{a{r}^2}=\frac{32}{4}\\ r^3=8\\ r=2\\ \\ \text{Substitute }r=2\text{ into (2),}\\ a{\left(2\right)}^2=4\\ a=1\end{array}$

Solution:
$$\begin{array}{l}\mathrm{}\end{array}$$

Solution:
$\begin{array}{l}3,12,48,\mathrm{.....}\\ GP,a=3,r=\frac{T_2}{T_1}=\frac{12}{3}=4\\ T_n>1000000\\ \left(3\right){\left(4\right)}^{n-1}>1000000\\ {\left(4\right)}^{n-1}>\frac{1000000}{3}\leftarrow \left[\left(3\right){\left(4\right)}^{n-1}\ne {12}^{n-1}\right]\\ \log 4^{n-1}>\log \frac{1000000}{3}\leftarrow (\text{Put log for both sides)}\\ \left(n-1\right)\lg 4>\lg \frac{1000000}{3}\leftarrow \left({\log }_a{m}^n=n{\log }_{a}m\right)\\ \left(n-1\right)\left(0.6021\right)>5.523\\ n-1>9.17\\ n>10.17\\ n=11\leftarrow (n\text{is an integer)}\\ \\ \boxed{\begin{array}{l}Check:\\ T_{11}=(3){\left(4\right)}^{10}\\ T_{11}=3145728>1000000\end{array}}\end{array}$

Question 1:
Diagram below shows part of an arrangement of bricks of equal size.



The number of bricks in the lowest row is 100. For each of the other rows, the number of bricks is 2 less than in the row below. The height of each brick is 7 cm.

Rahman builds a wall by arranging bricks in this way. The number of bricks in the highest row is 4. Calculate

(a) the height, in cm, of the wall.
(b) the total price of the bricks used if the price of one brick is 50 sen.

Solution:
100, 98, 96, …, 4 is an arithmetic progression
a = 100 and d = –2

(a)
T_n = 4
a + (n – 1) d = 4
100 + (n – 1)(–2) = 4
100 – 2n + 2 = 4
2n = 98
n = 49
Height of the wall = 49 × 7 = 343 cm

(b)
Total number of bricks used
= S₄₉
$=\frac{49}{2}\left(100+4\right)\leftarrow \boxed{S_n=\frac{n}{2}\left(a+l\right)}$
= 2548
Total price = 2548 × RM0.50
= RM1,274

Question 10:
In a geometric progression, the first term is 27 and the fourth term is 1. Calculate
(a) the positive value of common ratio, r,
(b) the sum of the first n terms where n is sufficiently large till $r^n\approx 0$

Solution:

Question 11:
Express the recurring decimal 0.187187187 … as a fraction in its simplest form.

Solution:

Question 12:
$\begin{array}{l}\text{Given that }\frac{1}{p}=\mathrm{0.1666666.....}\\ =q+a+b+c+\mathrm{.....}\end{array}$
where p is a positive integer. If q = 0.1 and a + b + c are the first three terms of a geometric progression, state the value of a, b and c in decimal form. Hence find the value of p.

Solution:

Question 1:
Diagram below shows part of an arrangement of bricks of equal size.



The number of bricks in the lowest row is 100. For each of the other rows, the number of bricks is 2 less than in the row below. The height of each brick is 7 cm.

Rahman builds a wall by arranging bricks in this way. The number of bricks in the highest row is 4. Calculate

(a) the height, in cm, of the wall.
(b) the total price of the bricks used if the price of one brick is 50 sen.


Solution:
100, 98, 96, …, 4 is an arithmetic progression
a = 100 and d = –2

(a)
T_n = 4
a + (n – 1) d = 4
100 + (n – 1)(–2) = 4
100 – 2n + 2 = 4
2n = 98
n = 49
Height of the wall = 49 × 7 = 343 cm

(b)
Total number of bricks used
= S₄₉
$=\frac{49}{2}\left(100+4\right)\leftarrow \boxed{S_n=\frac{n}{2}\left(a+l\right)}$
= 2548
Total price = 2548 × RM0.50
= RM1,274