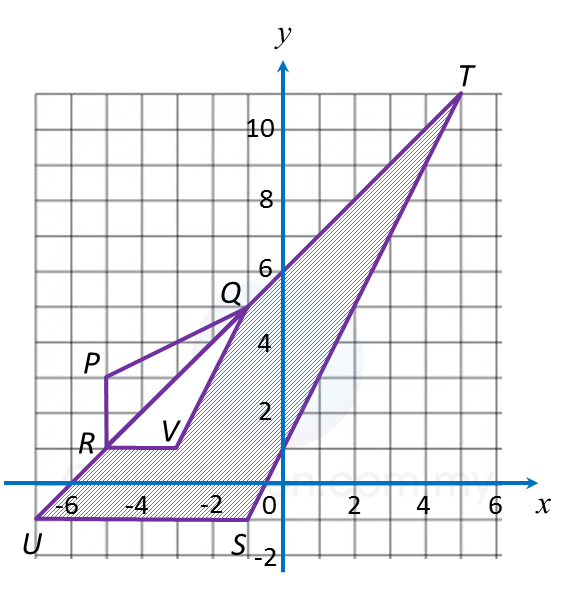
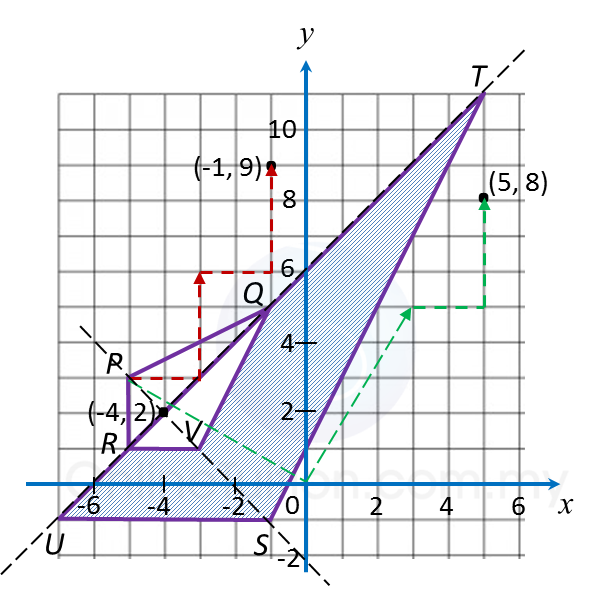
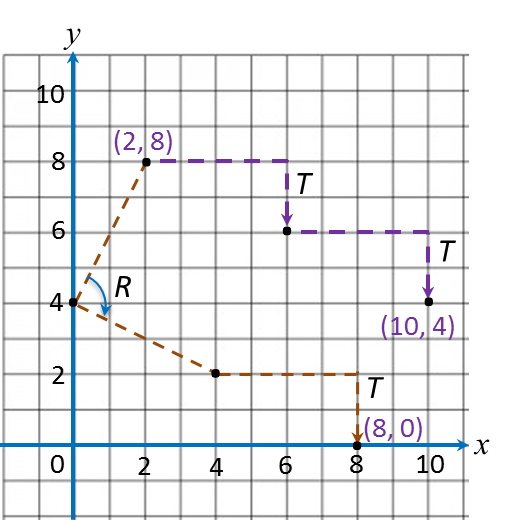
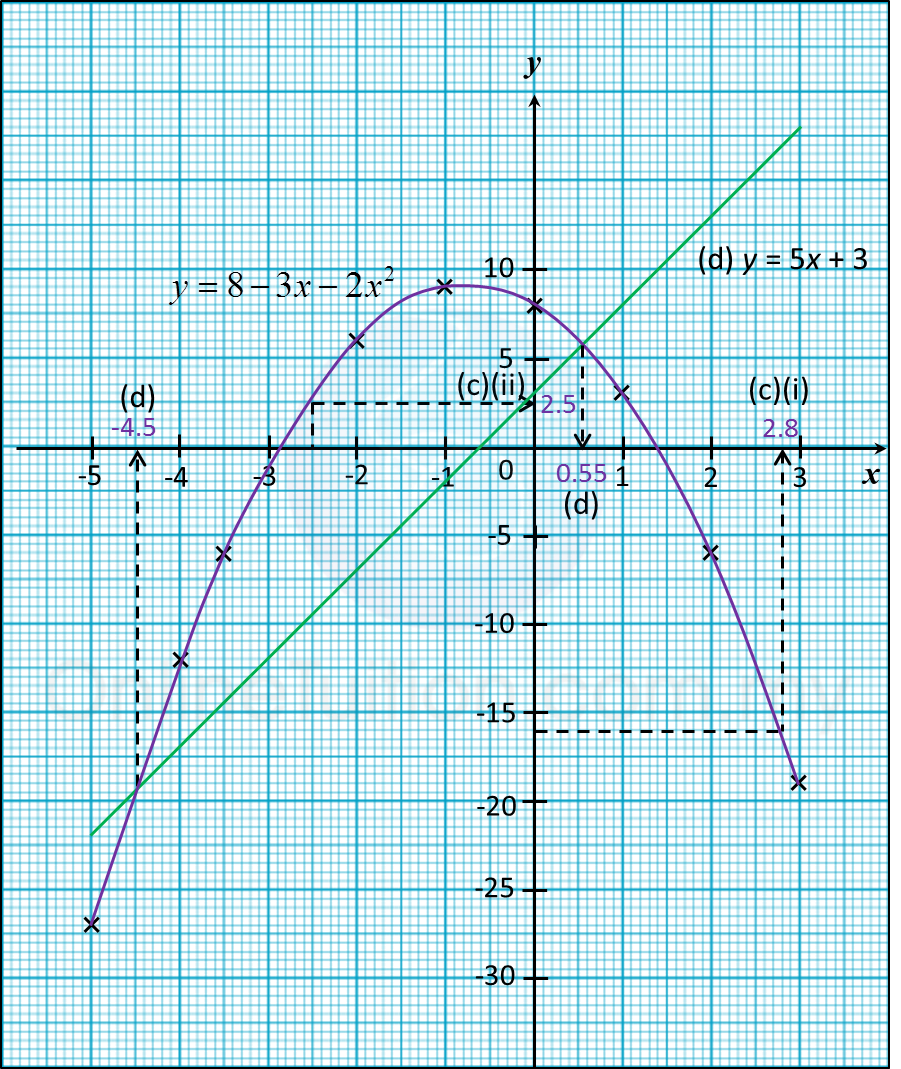
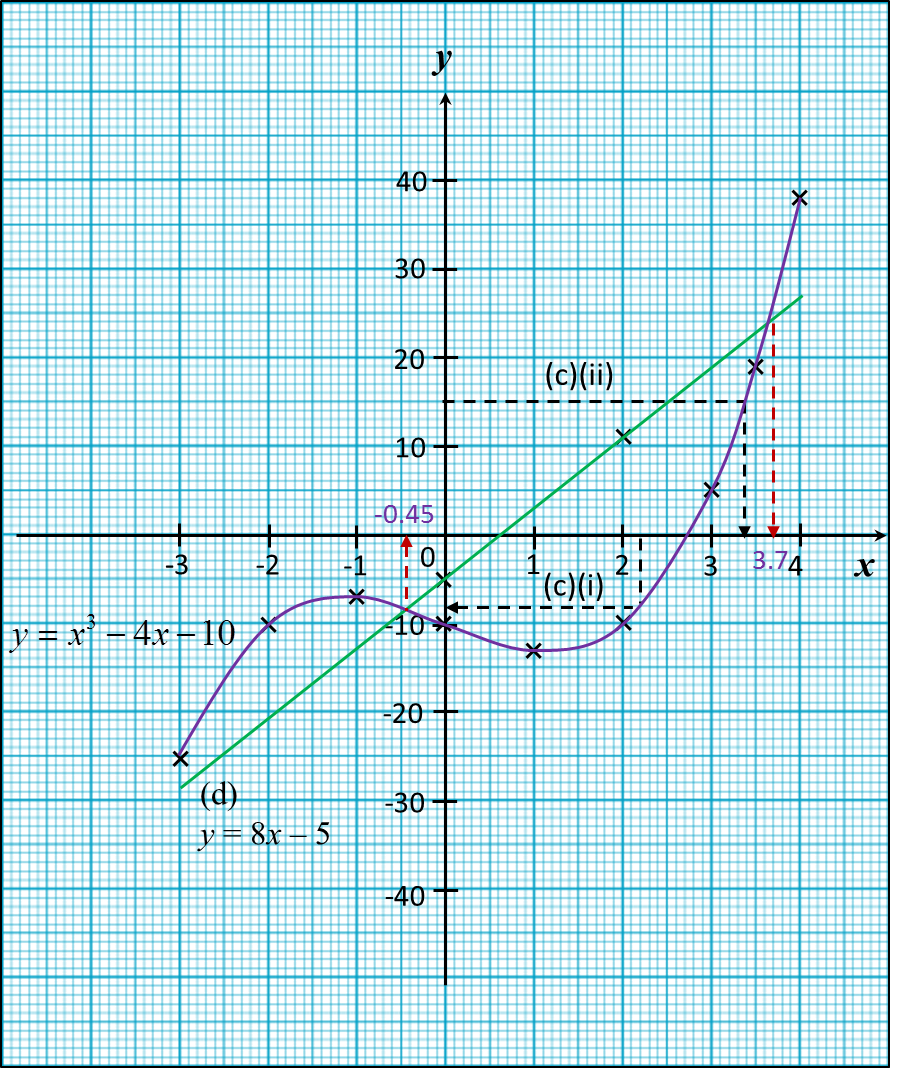
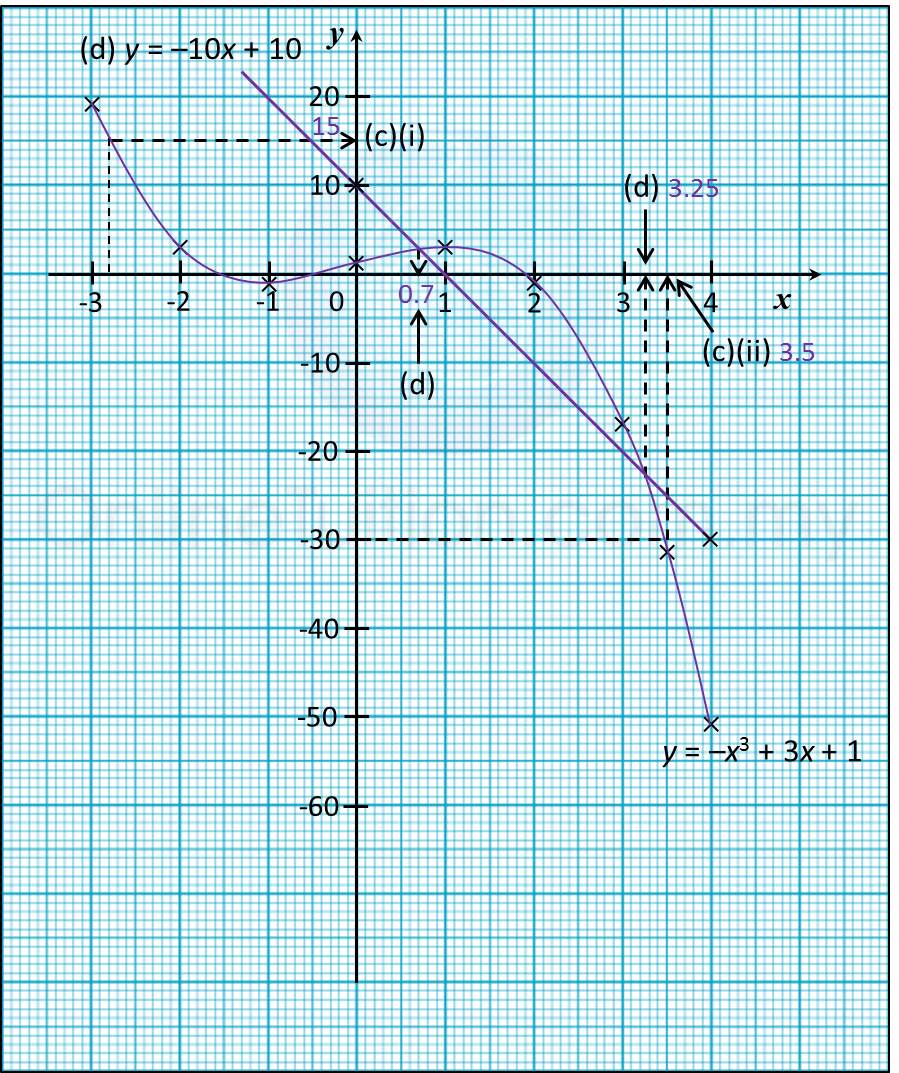
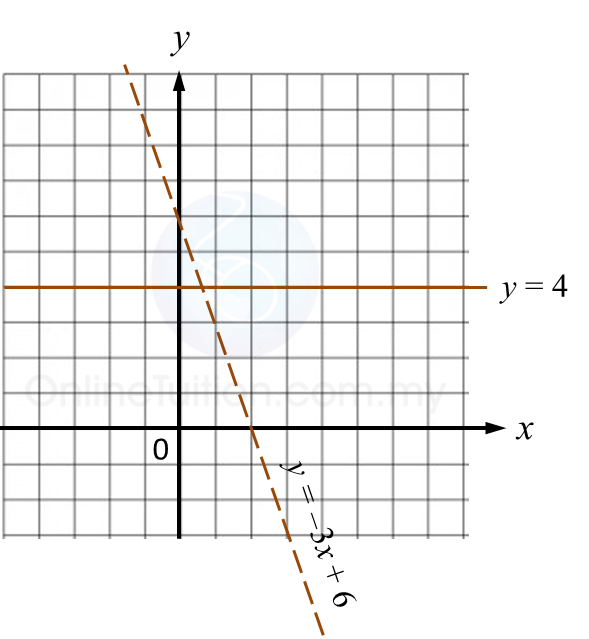
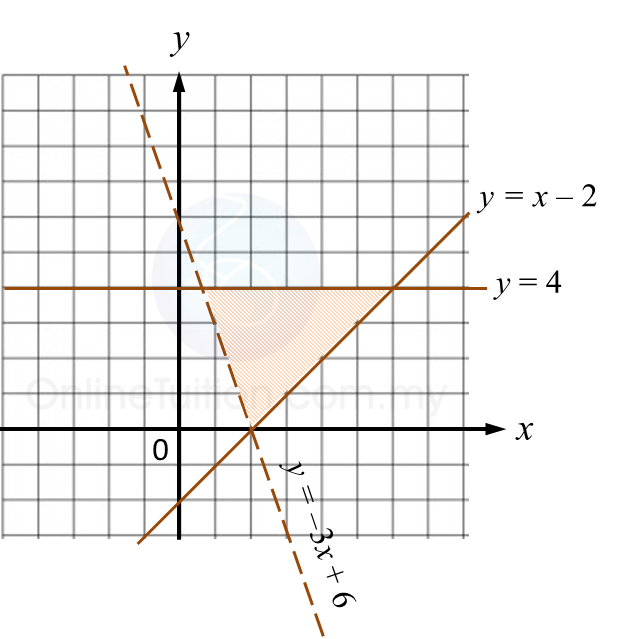
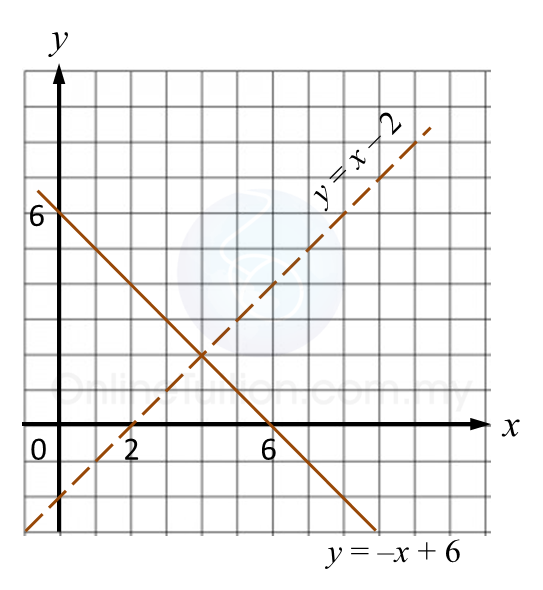
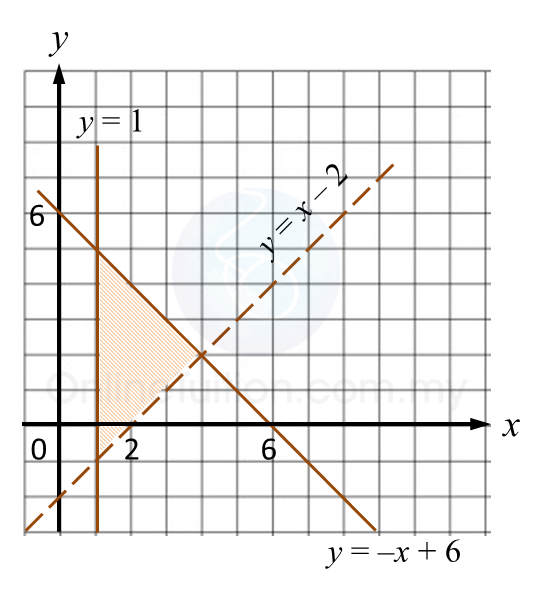
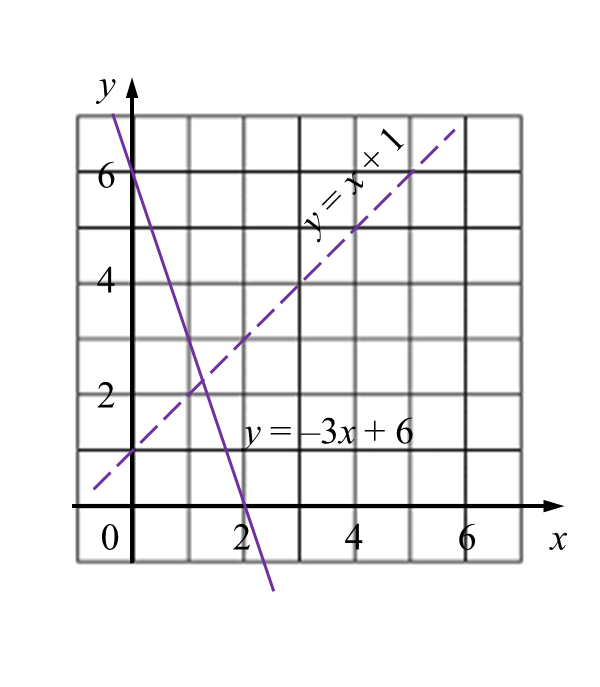
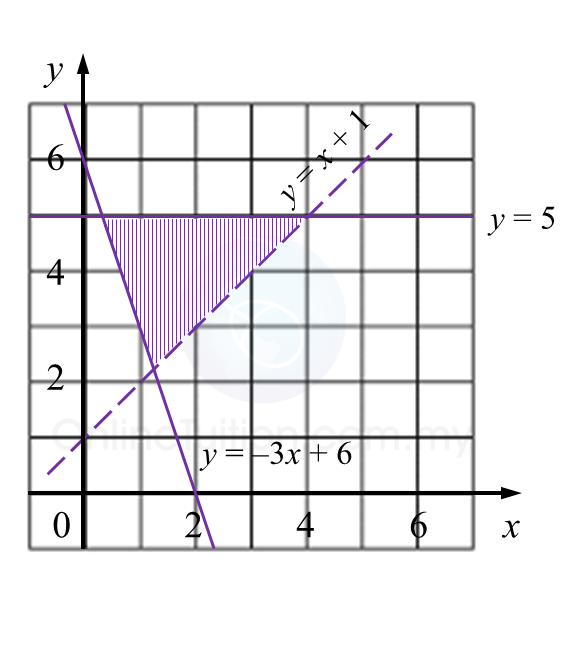
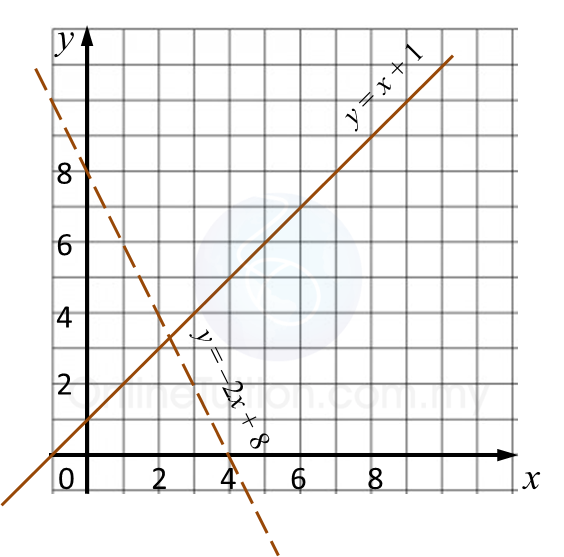
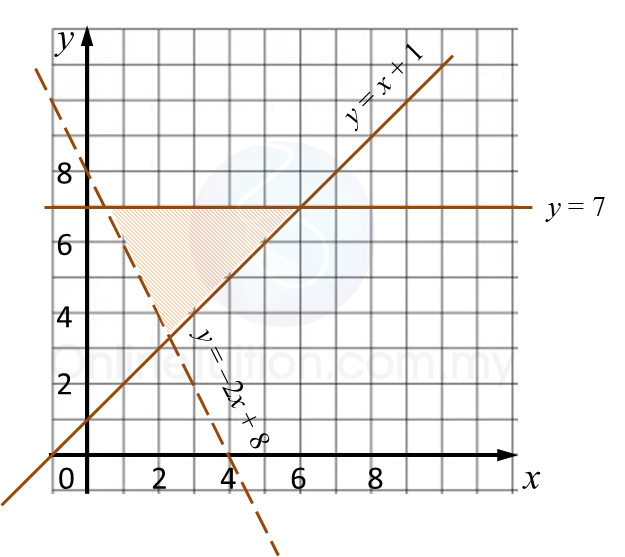
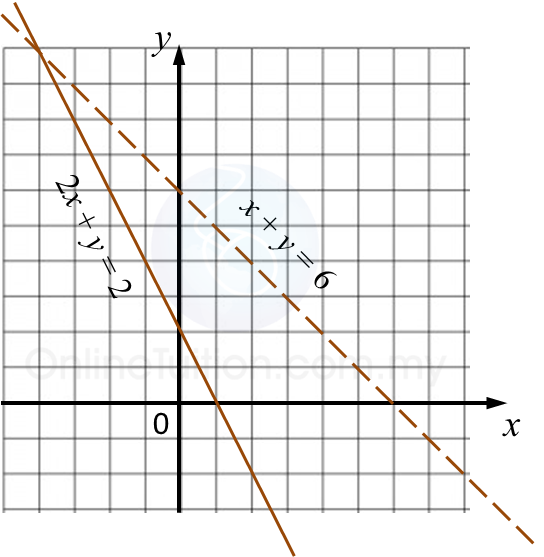
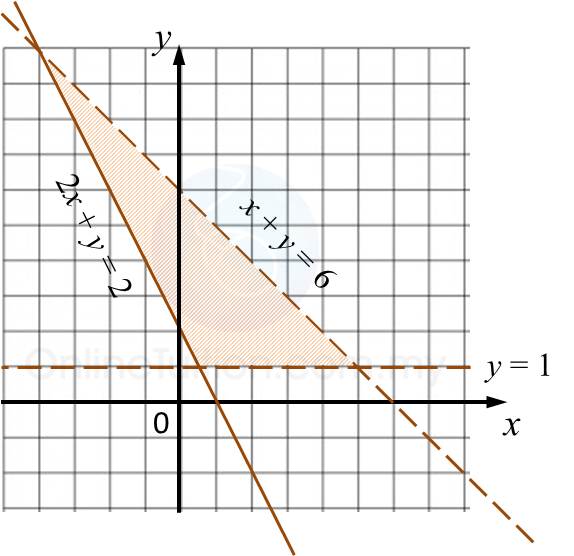
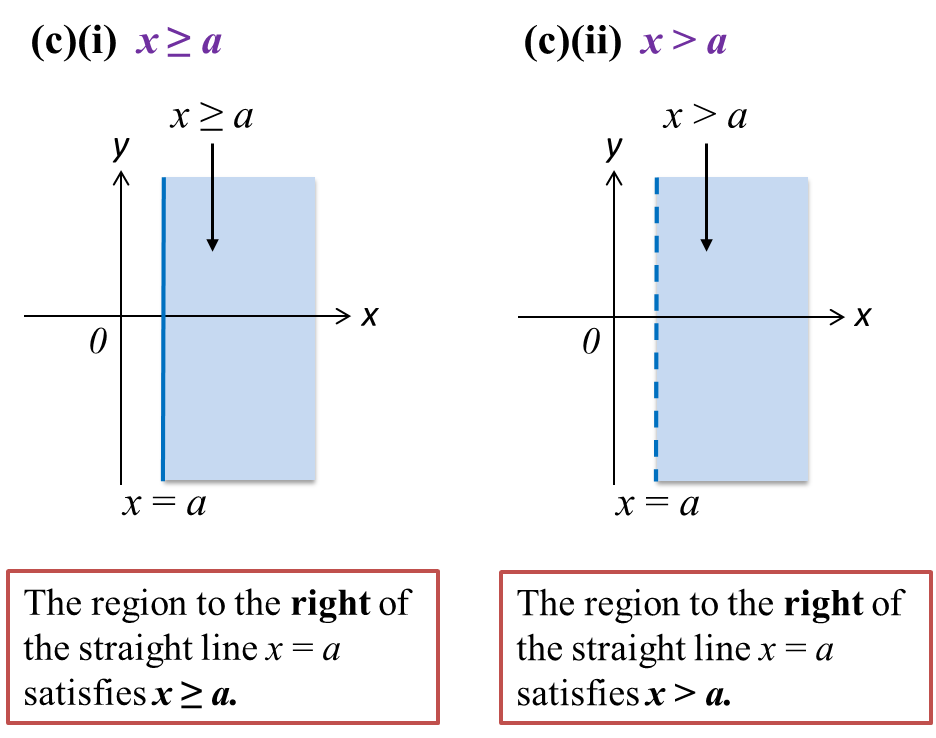
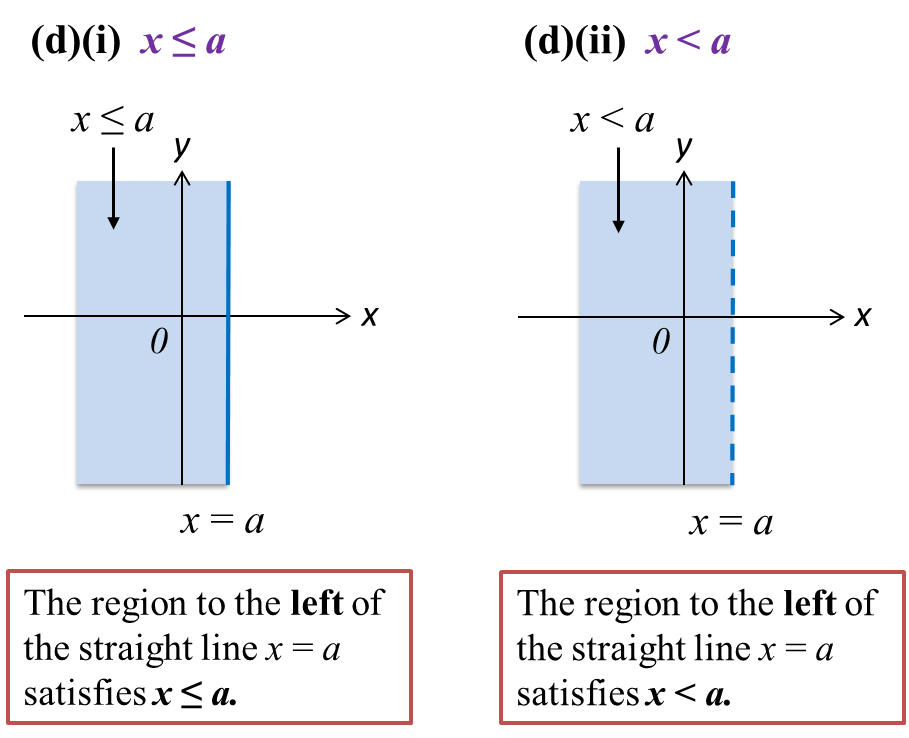
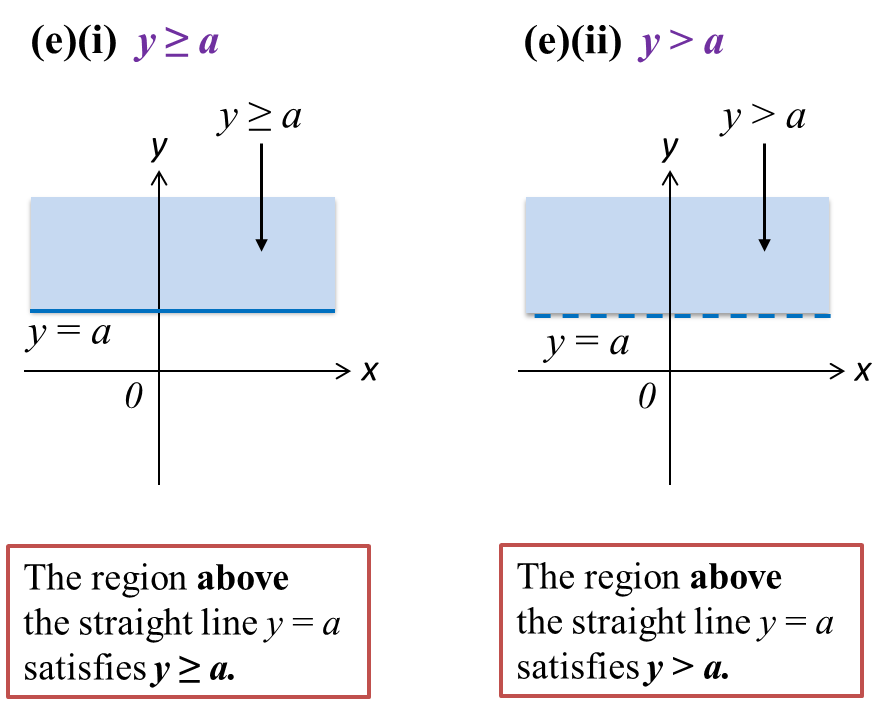
Question 5:
(a) Diagram below shows two points, M and N, on a Cartesian plane.
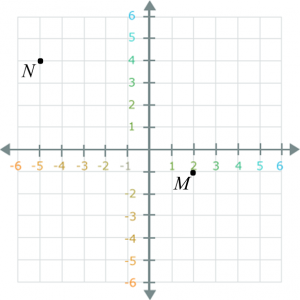
Transformation T is a translation and transformation R is an anticlockwise rotation of 90o about the centre (0, 2).
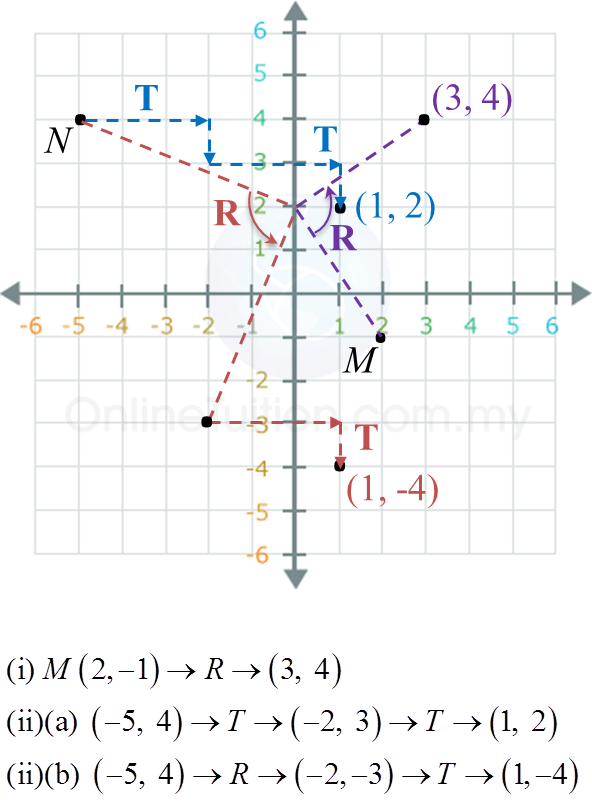
(i) State the coordinates of the image of point M under transformation R.
(ii) State the coordinates of the image of point N under the following transformations:
(a) T2,
(b) TR,
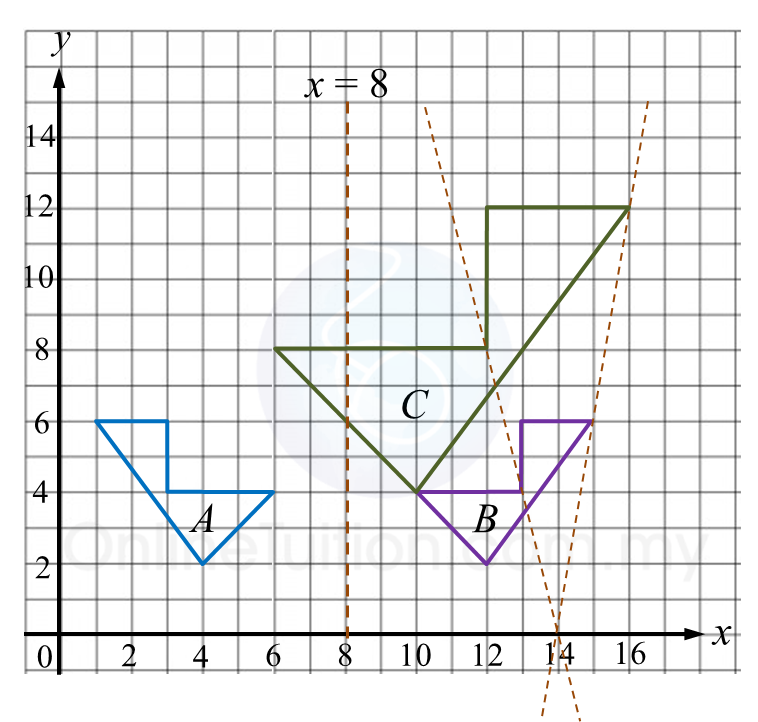
(b) Diagram below shows three pentagons, A, B and C, drawn on a Cartesian plane.

(i) C is the image of A under the combined transformation WV.
Describe in full the transformation:
(a) V (b) W
(ii) Given A represents a region of area 12 m2, calculate the area, in m2, of the region represented by C.
Solution:
(a)
(b)
(b)(i)(a)
V: A reflection in the line x = 8
(b)(i)(b)
W: An enlargement of scale factor 2 with centre (14, 0).
(b)(ii)
Area of B = area of A = 12 m2
Area of C = (Scale factor)2 x Area of object
= 22 x area of B
= 22 x 12
= 48 m2
(a) Diagram below shows two points, M and N, on a Cartesian plane.

Transformation T is a translation and transformation R is an anticlockwise rotation of 90o about the centre (0, 2).
(i) State the coordinates of the image of point M under transformation R.
(ii) State the coordinates of the image of point N under the following transformations:
(a) T2,
(b) TR,
(b) Diagram below shows three pentagons, A, B and C, drawn on a Cartesian plane.

(i) C is the image of A under the combined transformation WV.
Describe in full the transformation:
(a) V (b) W
(ii) Given A represents a region of area 12 m2, calculate the area, in m2, of the region represented by C.
Solution:
(a)

(b)

(b)(i)(a)
V: A reflection in the line x = 8
(b)(i)(b)
W: An enlargement of scale factor 2 with centre (14, 0).
(b)(ii)
Area of B = area of A = 12 m2
Area of C = (Scale factor)2 x Area of object
= 22 x area of B
= 22 x 12
= 48 m2