Question 6:
Diagram below shows trapezium ABCD.
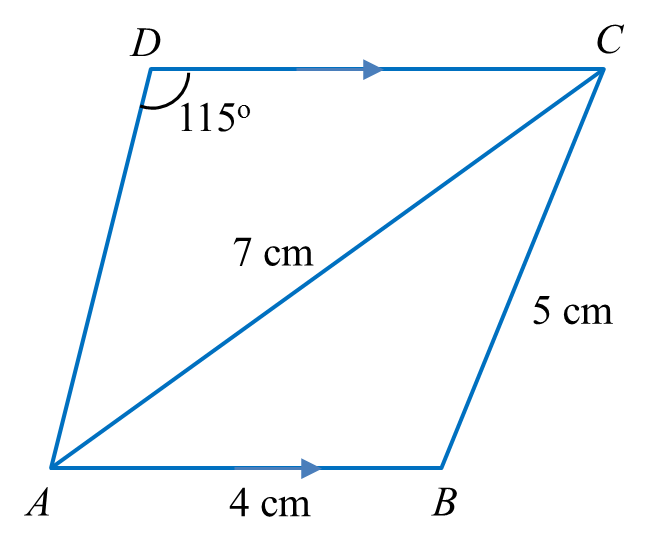 (a) Calculate
(a) Calculate
(i) ∠BAC.
(ii) the length, in cm, of AD.
(b) The straight line AB is extended to B’ such that BC = B’C.
(i) Sketch the trapezium AB’CD.
(ii) Calculate the area, in cm2, of ∆BB’C.
Solution:
(a)(i)
52=42+72−2(4)(7)cos∠BAC25=16+49−56cos∠BAC56cos∠BAC=40cos∠BAC=4056 ∠BAC=cos−14056 =44o25'
(a)(ii)
(b)(i)
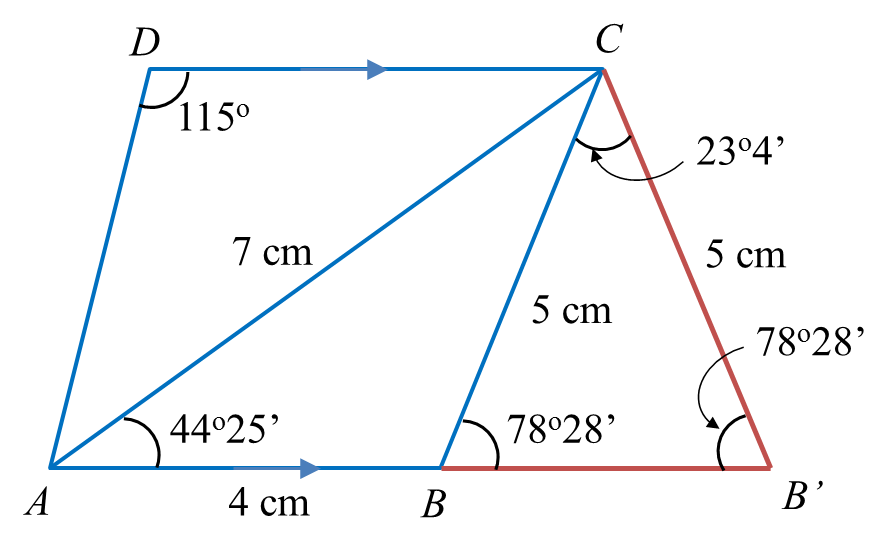
(b)(ii)
Diagram below shows trapezium ABCD.
 (a) Calculate
(a) Calculate(i) ∠BAC.
(ii) the length, in cm, of AD.
(b) The straight line AB is extended to B’ such that BC = B’C.
(i) Sketch the trapezium AB’CD.
(ii) Calculate the area, in cm2, of ∆BB’C.
Solution:
(a)(i)
52=42+72−2(4)(7)cos∠BAC25=16+49−56cos∠BAC56cos∠BAC=40cos∠BAC=4056 ∠BAC=cos−14056 =44o25'
(a)(ii)
(b)(i)

(b)(ii)