Question 10 (10 marks):
Diagram shows a curve y = 2x2 – 18 and the straight line PQ which is a tangent to the curve at point K.
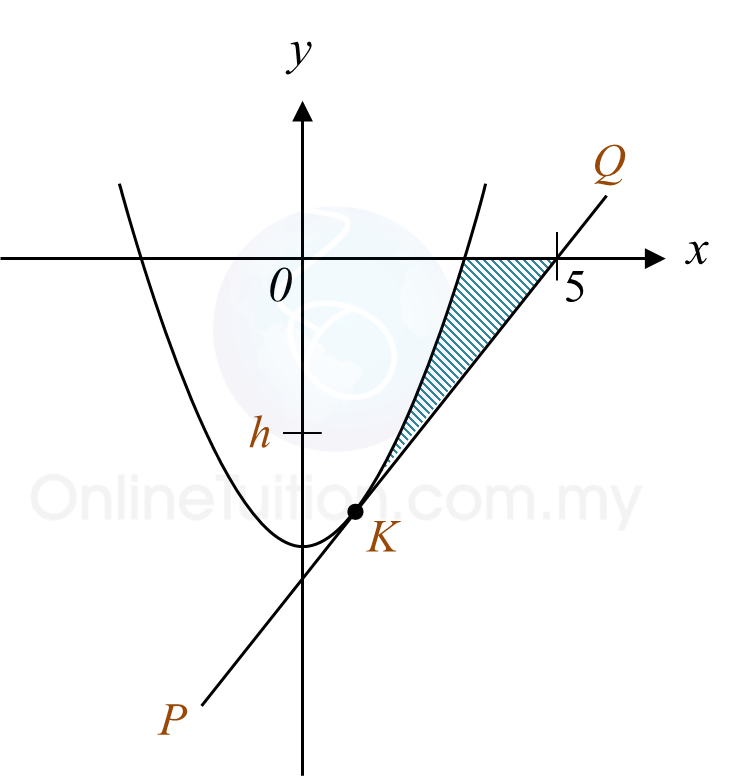
It is given that the gradient of the straight line PQ is 4.
(a) Find the coordinates of point K
(b) Calculate the area of the shaded region.
(c) When the region bounded by the curve, the x-axis and the straight line y = h is rotated through 180o about the y-axis, the volume generated is 65π unit3.
Find the value of h.
Solution:
(a)
y=2x2−18dydx=4xGradient of straight line PQ=44x=4x=1When x=1, y=2(1)2−18=−16Coordinates of K=(1,−16).
(b)
At x-axis, y=0∴
(c)
Diagram shows a curve y = 2x2 – 18 and the straight line PQ which is a tangent to the curve at point K.

It is given that the gradient of the straight line PQ is 4.
(a) Find the coordinates of point K
(b) Calculate the area of the shaded region.
(c) When the region bounded by the curve, the x-axis and the straight line y = h is rotated through 180o about the y-axis, the volume generated is 65π unit3.
Find the value of h.
Solution:
(a)
y=2x2−18dydx=4xGradient of straight line PQ=44x=4x=1When x=1, y=2(1)2−18=−16Coordinates of K=(1,−16).
(b)
At x-axis, y=0∴
(c)