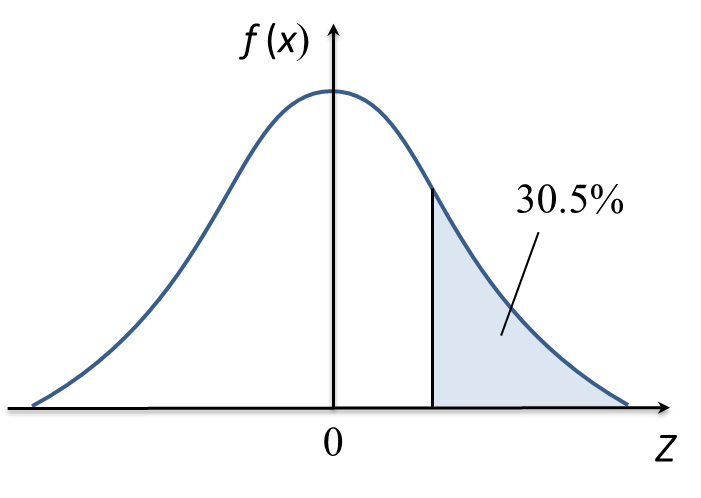
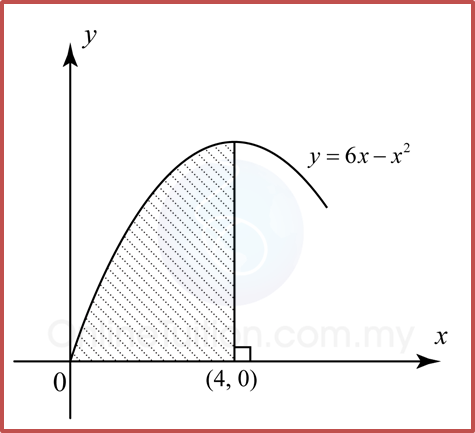
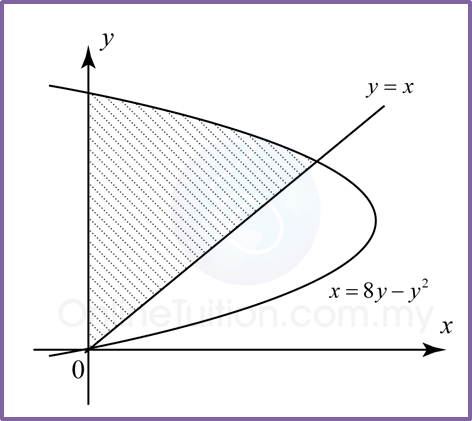
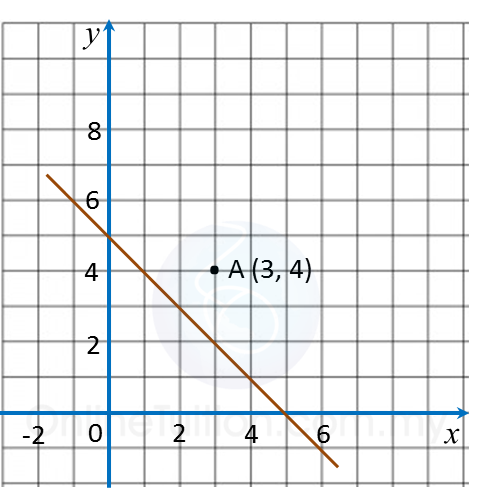
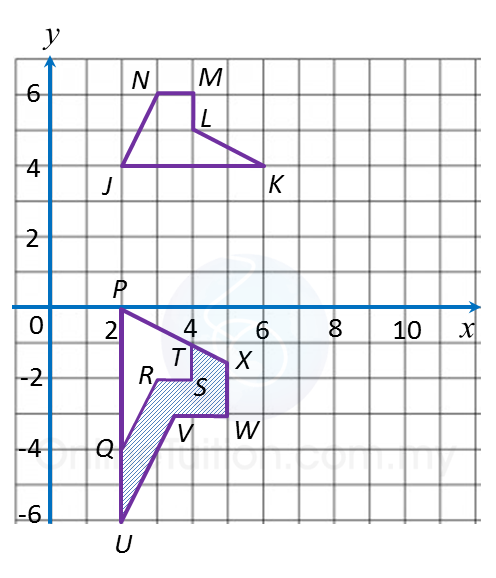
Bab 9 Pembezaan

Posted on June 9, 2020 by Myhometuition

Bab 9 Pembezaan

9.2.1 Terbitan Pertama untuk Fungsi Polinomial (Contoh)

Contoh:

Cari dy/dx bagi setiap fungsi yang berikut:

(a) y = 12

(b) y = x⁴

(d) y = 5x³

\begin{array}{l} (e) y = \frac{1}{x} \\ (f) y = \frac{2}{x^{4}} \\ (g) y = \frac{2}{5 x^{2}} \\ (h) y = 3 \sqrt{x} \\ (i) y = 4 \sqrt{x^{3}} \end{array}

Penyelesaian:

(a) y = 12

dy/dx = 0

(b) y = x⁴

dy/dx = 4x³

(c) y = 3x

dy/dx = 3

(d) y = 5x³

dy/dx = 15x²

(e)

\begin{array}{l} y = \frac{1}{x} = x^{- 1} \\ \frac{d y}{d x} = - x^{- 1 - 1} = - \frac{1}{x^{2}} \end{array}

(f)

\begin{array}{l} y = \frac{2}{x^{4}} = 2 x^{- 4} \\ \frac{d y}{d x} = - 4 (2 x^{- 4 - 1}) \\ = - 8 x^{- 5} = - \frac{8}{x^{5}} \end{array}

(g)

\begin{array}{l} y = \frac{2}{5 x^{2}} = \frac{2 x^{- 2}}{5} \\ \frac{d y}{d x} = - 2 (\frac{2 x^{- 2 - 1}}{5}) \\ = - \frac{4 x^{- 3}}{5} \\ = - \frac{4}{5 x^{3}} \end{array}

(h)

\begin{array}{l} y = 3 \sqrt{x} = 3 {(x)}^{\frac{1}{2}} \\ \frac{d y}{d x} = \frac{1}{2} (3 x^{\frac{1}{2} - 1}) \\ = \frac{3}{2} x^{- \frac{1}{2}} = \frac{3}{2 \sqrt{x}} \end{array}

(i)

\begin{array}{l} y = 4 \sqrt{x^{3}} = 4 {(x^{3})}^{\frac{1}{2}} = 4 x^{\frac{3}{2}} \\ \frac{d y}{d x} = \frac{3}{2} (4 x^{\frac{3}{2} - 1}) \\ = 6 x^{\frac{1}{2}} = 6 \sqrt{x} \end{array}

Bab 9 Pembezaan

Posted on June 9, 2020 by Myhometuition

9.4.1 Pembezaan Peringkat Kedua, Titik Pusingan: Titik Maksimum dan Titik Minimum (Contoh)

Contoh 1 (Nilai Maksimum suatu fungsi kuadratik)

Diberi bahawa y = 3x (4 – x), hitungkan

(a) nilai x apabila y adalah maksimum,

(b) nilai maksimum y.

Penyelesaian:

y = 3x (4 – x)

y = 12x – 3x²

\begin{array}{l} \frac{d y}{d x} = 12 - 6 x \\ Apabila y ialah maksimum, \frac{d y}{d x} = 0 \end{array}

0 = 12 – 6x

x = 2

y = 12x – 3x²

apabila x = 2,

y = 12 (2) – 3 (2)²

y = 12

Contoh 2 (Menentukan titik pusingan dan ujian terbitan kedua)

Cari koordinat titik-titik pusingan bagi lengkung y = 2x³+ 3x²– 12x + 7 dan tentukan jenis titik itu.

Penyelesaian:

\begin{array}{l} y = 2 x^{3} + 3 x^{2} - 12 x + 7 \\ \frac{d y}{d x} = 6 x^{2} + 6 x - 12 \\ di titik pusingan, \frac{d y}{d x} = 0 \end{array}

6x² + 6x – 12 = 0

x² + x – 2 = 0

(x – 1) (x + 2) = 0

x = 1 atau x = –2

apabila x = 1

y = 2 (1)³ + 3 (1)² – 12 (11) + 7

y = 0

(1, 0) ialah suatu titik pusingan.

apabila x = –2

y = 2 (–2)³ + 3 (–2)² – 12 (–2) + 7

y = 27

(-2, 27) ialah suatu titik pusingan.

\begin{array}{l} \frac{d^{2} y}{d x^{2}} = 12 x + 6 \\ Apabila x = 1, \\ \frac{d^{2} y}{d x^{2}} = 12 (1) + 6 = 18 > 0 (positif) \\ Oleh itu, titik pusingan (1, 0) adalah titik minimum . \end{array}

\begin{array}{l} Apabila x = - 2, \\ \frac{d^{2} y}{d x^{2}} = 12 (- 2) + 6 = - 18 < 0 (negatif) \\ Oleh itu, titik pusingan (-2, 27) adalah titik maksimum . \end{array}

8.4.5 Taburan Kebarangkalian, SPM Praktis (Kertas 2)

Posted on June 9, 2020 by Myhometuition

Soalan 12:
(a) Didapati bahawa 60% murid dari sebuah kelas tertentu mendapat gred A bagi Bahasa Inggeris dalam peperiksaan percubaan O level.
Jika 10 orang murid dari kelas itu dipilih secara rawak, cari kebarangkalian bahawa
(i) tepat 7orang murid mendapat gred A.
(ii) tidak lebih daripada 7 orang murid mendapat gred A.

(b) Rajah di bawah menunjukkan satu graf taburan normal piawai yang mewakili isi padu kicap dalam botol yang dihasilkan oleh sebuah kilang.

Diberi bahawa min ialah 950 cm³ dan variansnya ialah 256 cm⁶. Jika peratus isi padu yang melebihi V ialah 30.5%, cari
(i) nilai V,
(ii) kebarangkalian bahawa isi padu antara 930 cm³dan 960 cm³.

Penyelesaian:

\begin{array}{l} (a)(i) \\ P (X = r) = {}^{n}c_{r} . p^{r} . q^{n - r} \\ P (X = 7) = {}^{10}C_{7} {(0.6)}^{7} {(0.4)}^{3} \\ = 0.0860 \\ (i i) \\ P (X \leq 7) \\ = 1 - P (X > 7) \\ = 1 - P (X = 8) - P (X = 9) - P (X = 10) \\ = 1 - {}^{10}C_{8} {(0.6)}^{8} {(0.4)}^{2} - {}^{10}C_{9} {(0.6)}^{9} {(0.4)}^{1} - {}^{10}C_{10} {(0.6)}^{10} {(0.4)}^{0} \\ = 1 - 0.1209 - 0.0403 - 0.0060 \\ = 0.8328 \end{array}

\begin{array}{l} (b) (i) \\ P (X > V) = 30.5 % \\ P (Z > \frac{V - 950}{16}) = 0.305 \\ P (Z > 0.51) = 0.305 \\ \frac{V - 950}{16} = 0.51 \\ V = 0.51 (16) + 950 \\ = 958.16 {cm}^{3} \end{array}

\begin{array}{l} (i i) \\ Kebarangkalian \\ = P (930 < X < 960) \\ = P (\frac{930 - 950}{16} < Z < \frac{960 - 950}{16}) \\ = P (- 1.25 < Z < 0.625) \\ = 1 - P (Z > 1.25) - P (Z > 0.625) \\ = 1 - 0.1056 - 0.2660 \\ = 0.6284 \end{array}

8.4.5 Taburan Kebarangkalian, SPM Praktis (Kertas 2)

Posted on June 9, 2020 by Myhometuition

Soalan 11:
(a) 30% daripada pen di dalam sebuah kotak berwarna biru. Charlie memilih 4 batang pen secara rawak. Cari kebarangkalian sekurang-kurangnya satu batang pen yang dipilih tidak berwarna biru.

(b) Jisim betik yang dituai dari sebuah ladang buah-buahan adalah mengikut taburan normal dengan min 2 kg dan sisihan piawai h kg. Diberi bahawa 15.87% daripada betik itu mempunyai jisim lebih daripada 2.5 kg.
(i) Hitung nilai h.
(ii) Diberi bilangan betik yang dituai dari lading buah-buahan itu ialah 1320, cari bilangan betik yang mempunyai jisim antara 1.0 kg hingga 2.5 kg.

Penyelesaian:

\begin{array}{l} (a) \\ P (X \geq 1) = 1 - P (X = 0) \\ = 1 - {}^{4}C_{4} {(0.3)}^{4} {(0.7)}^{0} \\ = 0.9919 \end{array}

\begin{array}{l} (b) μ = 2, σ = h \\ (i) \\ P (X > 2.5) = 15.87 % \\ P (Z > \frac{2.5 - 2}{h}) = 0.1587 \\ P (Z > 1.0) = 0.1587 \\ \frac{2.5 - 2}{h} = 1.0 \\ h = 0.5 \end{array}

\begin{array}{l} (i i) \\ p = P (1.0 < x < 2.5) \\ = P (\frac{1.0 - 2}{0.5} < Z < \frac{2.5 - 2}{0.5}) \\ = P (- 2 < Z < 1) \\ = 1 - P (Z < - 2) - P (Z > 1) \\ = 1 - P (Z > 2) - P (Z > 1) \\ = 1 - 0.0228 - 0.1587 \\ = 0.8185 \\ Bilangan betik = 0.8185 \times 1320 \\ = 1080 \end{array}

8.4.5 Taburan Kebarangkalian, SPM Praktis (Kertas 2)

Posted on June 9, 2020 by Myhometuition

Soalan 10:
(a) Satu tinjauan dijalankan berkenaan kelab bulan sabit merah di sebuah sekolah.
Didapati bahawa min bilangan ahli kelab bulan sabit merah ialah 315, varians ialah 126 dan kebarangkalian seorang murid menyertai kelab bulan sabit merah ialah p.

(i) Cari nilai p.

(ii) Jika 8 orang murid dari sekolah itu dipilih secara rawak, cari kebarangkalian lebih daripada 5 orang murid menyertai kelab bulan sabit merah.

(b) Jisim baja yang digunakan di sebuah dusun buah-buahan mempunyai taburan normal dengan min 5 kg dan varians 0.8 kg. Cari kebarangkalian dalam satu hari tertentu, lebih daripada 6 kg baja digunakan.

Penyelesaian:

\begin{array}{l} (a)(i) \\ n p = 315 \\ n p (1 - p) = 126 \\ 315 (1 - p) = 126 \\ 1 - p = \frac{126}{315} \\ 1 - p = 0.4 \\ p = 0.6 \\ (i i) \\ n = 8, p = 0.6 \\ P (X = r) = {}^{n}c_{r} . p^{r} . q^{n - r} \\ P (X = r) = {}^{8}C_{r} {(0.6)}^{r} {(0.4)}^{8} \\ P (X > 5) \\ = P (X = 6) + P (X = 7) + P (X = 8) \\ = {}^{8}C_{6} {(0.6)}^{6} {(0.4)}^{2} + {}^{8}C_{7} {(0.6)}^{7} {(0.4)}^{1} + {}^{8}C_{8} {(0.6)}^{8} {(0.4)}^{0} \\ = 0.20902 + 0.08958 + 0.01680 \\ = 0.3154 \end{array}

\begin{array}{l} (b) \\ P (X > 6) = P (Z > \frac{6 - 5}{\sqrt{0.8}}) \\ = P (Z > 1.12) \\ = 0.1314 \end{array}

Bab 16 Fungsi Trigonometri

Posted on June 8, 2020 by Myhometuition

5.3.2b Melakar Graf Fungsi Trigonometri (Bahagian 2)

Contoh:

Lakarkan graf bagi setiap fungsi trigonometri yang berikut untuk 0 ≤ x ≤ 2π.

(g) y = –sin x
(h) y = –kos x

(i) y = | sin x |
(j) y = | kos x |

(k) y = tan 2x

Penyelesaian:

(g) y = –sin x

(h) y = –kos x

(i) y = | sin x |

(j) y = | kos x |

(k) y = tan 2x

Bab 15 Vektor

Posted on June 7, 2020 by Myhometuition

4.4.1 Pengungkapan Suatu Vektor sebagai Gabungan Linear Vektor yang lain (Contoh)

Contoh:

Rajah di bawah menunjukkan sebuah segiempat selari ABCD. Titik Q terletak pada garis lurus AB dan titik S terletak pada garis lurus DC. Garis lurus AS dipanjangkan ke titik T dengan keadaan AS = 2ST.

Diberi bahawa AQ : QB = 3 : 1, DS : SC = 3 : 1,

\vec{A Q} = 6 \underset{˜}{a} dan \vec{A D} = \underset{˜}{b}

(a) Ungkapan dalam sebutan

\underset{˜}{a} dan \underset{˜}{b} :

(i) \vec{A S} (ii) \vec{Q C}

(b) Seterusnya, tunjukkan titik Q, C dan T adalah segaris.

Penyelesaian:

(a)(i)

\begin{array}{l} \vec{A S} = \vec{A D} + \vec{D S} \\ = \vec{A D} + \vec{A Q} \leftarrow \begin{array}{l} A Q : Q B = 3 : 1 dan \\ D S : S C = 3 : 1 \\ ∴ \vec{A Q} = \vec{D S} \end{array} \\ = \underset{˜}{b} + 6 \underset{˜}{a} \\ = 6 \underset{˜}{a} + \underset{˜}{b} \end{array}

(a)(ii)

\begin{array}{l} \vec{Q C} = \vec{Q B} + \vec{B C} \\ = \frac{1}{3} \vec{A Q} + \vec{A D} \leftarrow \begin{array}{l} A Q : Q B = 3 : 1 \\ \frac{A Q}{Q B} = \frac{3}{1} \Rightarrow Q B = \frac{1}{3} A Q \\ bagi segiempat selari, \\ B C / / A D, B C = A D \end{array} \\ = \frac{1}{3} (6 \underset{˜}{a}) + \underset{˜}{b} \\ = 2 \underset{˜}{a} + \underset{˜}{b} \end{array}

(b)

\begin{array}{l} \vec{Q T} = \vec{Q A} + \vec{A T} \\ = \vec{Q A} + \frac{3}{2} \vec{A S} \leftarrow \begin{array}{l} A S = 2 S T \\ A T = 3 S T = \frac{3}{2} A S \end{array} \\ = - 6 \underset{˜}{a} + \frac{3}{2} (6 \underset{˜}{a} + \underset{˜}{b}) \\ = 3 \underset{˜}{a} + \frac{3}{2} \underset{˜}{b} \\ = \frac{3}{2} (2 \underset{˜}{a} + \underset{˜}{b}) \\ = \frac{3}{2} \vec{Q C} \\ Maka Q, C dan T adalah segaris . \end{array}

Bab 14 Pengamiran

Posted on June 7, 2020 by Myhometuition

3.5.1 Pengamiran Sebagai Penghasiltambahan Luas (Contoh)

Contoh 1:

Cari luas rantau berlorek.

Penyelesaian:

Luas rantau berlorek, L

\begin{array}{l} = \int_{a}^{b} y d x \\ = \int_{0}^{4} (6 x - x^{2}) d x \\ = {[\frac{6 x^{2}}{2} - \frac{x^{3}}{3}]}_{0}^{4} \\ = [3 {(4)}^{2} - \frac{{(4)}^{3}}{3}] - 0 \\ = 26 \frac{2}{3} {unit}^{2} \end{array}

Contoh 2:

Cari luas rantau berlorek.

Penyelesaian:

y = x -----(1)

x = 8y – y² -----(2)

Gantikan (1) ke dalam (2),

y = 8y – y²

y²– 7y = 0

y (y – 7) = 0

y = 0 atau 7

Dari (1), x = 0 atau 7

Maka, titik persilangan antara lengkung dengan garis lurus ialah (0, 0) dan (7, 7).

Titik persilangan lengkung dengan paksi-y adalah,

x = 8y – y²

pada y-axis, x = 0

0 = 8y – y²

y (y – 8) = 0

y = 0 atau 8

Luas kawasan berlorek = (A₁) Luas segitiga + (A₂) Luas di bawah lengkung dari y = 7 hingga y = 8.

\begin{array}{l} = \frac{1}{2} \times tapak \times tinggi + \int_{7}^{8} x d y \\ = \frac{1}{2} \times (7) (7) + \int_{7}^{8} (8 y - y^{2}) d y \\ = \frac{49}{2} + {[\frac{8 y^{2}}{2} - \frac{y^{3}}{3}]}_{7}^{8} \\ = 24 \frac{1}{2} + [4 {(8)}^{2} - \frac{{(8)}^{3}}{3}] - [4 {(7)}^{2} - \frac{{(7)}^{3}}{3}] \\ = 24 \frac{1}{2} + 85 \frac{1}{3} - 81 \frac{2}{3} \\ = 28 \frac{1}{6} {unit}^{2} \end{array}

3.4.10 SPM Praktis, Penjelmaan (Soalan Panjang)

Posted on June 6, 2020 by Myhometuition

Soalan 10:
(a) Rajah di bawah menunjukkan titik A dan garis lurus y + x = 5 dilukis pada suatu satah Cartesan.

Penjelmaan T ialah satu translasi

(\begin{array}{l} 5 \\ - 2 \end{array})

Penjelmaan R ialah satu pantulan pada garis lurus y + x = 5.
Nyatakan koordinat imej bagi titik A di bawah setiap penjelmaan berikut:
(i) Penjelmaan T,
(ii) Penjelmaan gabungan TR.

(b) Rajah di bawah menunjukkan pentagon JKLMN, PQRST dan PUVWX, dilukis pada suatu satah Cartesan.

(i) PUVWX ialah imej bagi JKLMN di bawah gabungan penjelmaan CB.
Huraikan selengkapnya penjelmaan:
(a) B
(b) C

(ii) Diberi bahawa pentagon JKLMN mewakili suatu kawasan yang mempunyai luas 80 m² .
Hitungkan luas, dalam m² , kawasan yang diwakili oleh rantau berlorek.

Penyelesaian:
(a)

(i) (3, 4) → T → (8, 2)
(ii) (3, 4) → R → (1, 2) → T → (6, 0)

(b)

(b)(i)(a)
B: Putaran ikut arah jam melalui 90^o pada pusat (0, 2).

(b)(i)(b)

\begin{array}{l} Factor skala = \frac{P U}{P Q} = \frac{6}{4} = \frac{3}{2} \\ C: Satu pembesaran pada pusat P (2, 0) dengan faktor skala \frac{3}{2} . \end{array}

(b)(ii)
Luas PQRST = Luas JKLMN = 80 m²

\begin{array}{l} Luas P U V W X \\ = {(\frac{3}{2})}^{2} \times luas P Q R S T \\ = \frac{9}{4} \times 80 \\ = 180 m^{2} \\ ∴ Luas rantau berlorek \\ = luas of P U V W X - luas P Q R S T \\ = 180 - 80 \\ = 100 m^{2} \end{array}

3.4.9 SPM Praktis, Penjelmaan (Soalan Panjang)

Posted on June 6, 2020 by Myhometuition

Soalan 9:
Rajah menunjukkan tiga segi tiga RPQ, UST dan RVQ, dilukis pada suatu satah Cartes.

(a) Penjelmaan R ialah satu putaran 90^o , ikut arah jam pada pusat O.
Penjelmaan T ialah satu translasi

(\begin{array}{l} 2 \\ 3 \end{array})

Nyatakan koordinat imej bagi titik P di bawah setiap penjelmaan berikut:
(i) T² ,
(ii) TR.

(b)(i) Segi tiga UST ialah imej bagi segi tiga RPQ di bawah gabungan penjelmaan VW.
Huraikan selengkapnya penjelmaan:
(a) W (b) V

(ii) Diberi bahawa segi tiga RPQ mewakili suatu kawasan yang mempunyai luas 15 m² .
Hitungkan luas, dalam m² , kawasan yang diwakili oleh rantau berlorek.

Penyelesaian:
(a)

(a)(i)
(–5, 3) → T → (–3, 6) ) → T → (–1, 9)

(a)(ii)
(–5, 3) → R → (3, 5) → T → (5, 8)

(b)(i)(a)
W: Satu pantulan pada garis lurus URQT.

(b)(i)(b)

\begin{array}{l} Factok skala = \frac{U S}{R V} = \frac{6}{2} = 3 \\ V: Satu pembesaran pada pusat (- 4, 2) dengan faktor skala 3 . \end{array}

(b)(ii)
Luas UST = (faktor skala)² x Luas objek RPQ
= 3² x luas objek RPQ
= 3² x 15
= 135 m²

Oleh itu,
Luas rantau berlorek
= Luas UST – luas RPQ
= 135 – 15
= 120 m²