Home › View all posts by Myhometuition › Page 11

Author: Myhometuition

5.5 Parallel Lines (Part 2)

Posted on by
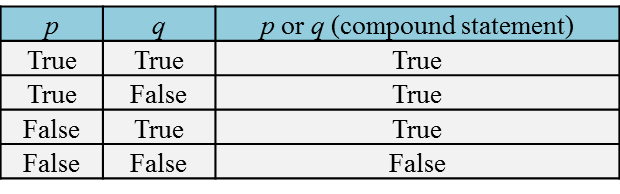
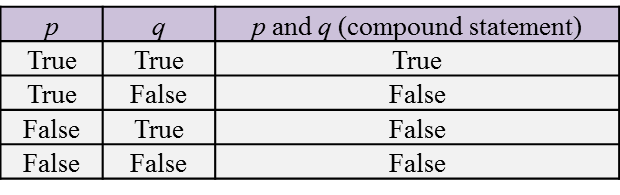
(B) Equation of Parallel Lines
 
To find the equation of the straight line which passes through a given point and parallel to another straight line, follow the steps below:
 
Step 1 : Let the equation of the straight line take the form y = mx + c.
Step 2 : Find the gradient of the straight line from the equation of the straight line parallel to it.
Step 3 : Substitute the value of gradient, m, the x-coordinate and y-coordinate of the given point into y = mx + c to find the value of the y-intercept, c.
Step 4 : Write down the equation of the straight line in the form y = mx + c.
 
Example 2:
Find the equation of the straight line that passes through the point (–8, 2) and is parallel to the straight line 4y + 3x = 12.

Solution:
4y+3x=12 4y=−3x+12 y=− 3 4 x+3 ∴m=− 3 4 At (−8,2), substitute m=− 3 4 , x=−8, y=2 into: y=mx+c 2=− 3 4 ( −8 )+c c=2−6 c=−4 ∴ The equation of the staright line is y=− 3 4 x−4.

4.6 SPM Practice (Long Questions)

Posted on by

Question 9:
(a) State whether the following statements are true statement or false statement.
( i ) { }⊂{ H,O,T } ( ii ) { 2 }⊂{ 2,3,4 }={ 2,3,4 }

(b) Complete the following statement to form a true statement by using the quantifier ‘all’ or ‘some’.
   ……… factor of 24 are factor of 40

(c) Write down two implications based on the following compound statement.

The perimeter of square ABCD is 60 cm if and only if the side of square ABCD is 15 cm.
(d) It is given that the volume of the sphere is 4 3 π r 3 where r is the radius.
Make one conclusion by deduction for the volume of the sphere with radius 3 cm.

Solution:
(a)(i) True

(a)(ii) False

(b)    …Some… factor of 24 are factor of 40

(c)(i) If the perimeter of square ABCD is 60 cm, then the side of square ABCD is 15 cm.

(c)(ii) If the side of square ABCD is 15 cm, then the perimeter of square ABCD is 60 cm.

(d)
 4 3 π× 3 3 =36π Volume of the sphere is 36π.    



Question 10:
(a)(i) State whether the following compound statement is true or false.

   All straight lines have positive gradients.
(ii) Write down the converse of the following implication.

If x = 5, then x2 = 25.
(b) Write down Premise 2 to complete the following argument:
Premise 1: If Q is an odd number, then 2 × Q is an even number.
Premise 2: _____________________
Conclusion: 2 × 3 is an even number.

(c) Make a general conclusion by induction for the sequence of numbers 4, 18, 48, 100, … which follows the following pattern.
4 = 1 (2)2
18 = 2 (3)2
48 = 3 (4)2
100 = 4 (5)2
   .
   .
   .

Solution:
(a)(i) False

(a)(ii) If x2 = 25, then x = 5

(b) Premise 2: 3 is an odd number

(c) n (n + 1)2, where n = 1, 2, 3, …


4.5.1 Argument (Sample Questions)

Posted on by

Example 1:
Complete the conclusion in the following argument:
Premise 1: All regular polygons have equal sides.
Premise 2: ABCD is a regular polygon.
Conclusion:
Solution:
Conclusion: ABCD has equal sides.



Example 2:
Complete the conclusion in the following argument:
Premise 1: If m > 4, then 2m > 8.
Premise 2: 2m < 8
Conclusion:
Solution:
Conclusion: m < 4.


Example 3:
Complete the premise in the following argument:
Premise 1:
Premise 2: m ×n is not an even number.
Conclusion: m and n are not even numbers.
Solution:
Premise 1: If m and n are even numbers, then m ×n is an even number.
 
 
 
Example 4:
Complete the premise in the following argument:
Premise 1: If x = 3, then x2 = 9.
Premise 2:
Conclusion: x ≠ 3
Solution:
Premise 2: x2 ≠ 9.

4.4.1 Implications (Sample Questions)

Posted on by

Example 1:
Write down two implications based on the following statement.
y3 = -125 if and only if y = -5.

Solution:
Implication 1: If y3 = -125, then y = -5.
Implication 2: If y = -5, then y3 = -125. 



Example 2:
Write down two implications based on the following statement.
8 is a factor of 24 if and only if 24 can be divided exactly by 8.

Solution:
Implication 1: 8 is a factor of 24 if 24 can be divided exactly by 8.
Implication 2: 24 can be divided exactly by 8 if 8 is a factor of 24.



Example 3:
State the converse of the following statement and hence, determine whether its converse is true or false.
(a) If 2x > 8, then x > 4.
(b) If x is a multiple of 6, then it is a multiple of 3.

Solution:
(a) Converse implication: If x > 4, then 2x > 8.
 The converse is true.
(b) Converse implication: If x is a multiple of 3, then it is multiple of 6.
 The converse is false. (9 is a multiple of 3 but it is not a multiple of 6) 

4.3 Operations on Statements (Sample Questions 2)

Posted on by

Example 3:
Determine whether each of the following statements is true or false.
(a) 3 × (-4) = -12 and 13 + 6 = 19
(b) 100 × 0.7 = 70 and 12 + (-30) = 18

Solution:
When two statements are combined using ‘and’, a true compound statement is obtained only if both statements are true.
If one or both statements are false, then the compound statement is false.

(a) Both the statements ‘3 × (-4) = -12’ and ‘13 + 6 = 19’ are true. Therefore, the statement ‘3 × (-4) = -12 and 13 + 6 = 19’ is true.

(b) The statement ‘12 + (-30) = 18’ is false. Therefore, the statement ‘100 × 0.7 = 70 and 12 + (-30) = 18’ is false.



Example 4:
Determine whether each of the following statements is true or false.
(a) m + m = m2 or p × p × p = p-3
(b)  64 3 =−4 or  −27 3 =−3

Solution:
When two statements are combined using ‘or’, a false compound statement is obtained only if both statements are false.
If one or both statements are true, then the compound statement is true.

(a) Both the statements ‘m+ m = m2’ and ‘p × p × p= p-3’ are false. Therefore the statement m + m = m2 or p × p × p = p-3 is false.

(b) The statement  ' − 27 3 = − 3 '  is true. Therefore, the statement  64 3 =−4 or  −27 3 =−3  is true.

4.3 Operations on Statements

Posted on by
4.3 Operations on Statements (Part 3)

(C) Truth Values of Compound Statements using ‘Or’
 
1. When two statements are combined using ‘or’, a false compound statement is obtained only if both statements are false.
 
2. f one or both statements are true, then the compound statement is true.
 
The truth table:
Let p = statement 1 and q= statement 2.
The truth values for ‘p’ or ‘q’ are as follows:


 
Example 6:
Determine the truth value of the following statements.
(a) 60 is divisible by 4 or 9.
(b) 53 = 25 or 43 = 64.
(c) 5 + 7 > 14 or √9 = 2.
 
Solution:
(a)
60 is divisible by 4  ← (p is true)
60 is divisible by 9  ← (q is false)
Therefore, 60 is divisible by 4 or 9 is a true statement. (‘p or q’ is true)
 
(b)
53 = 25  ← (p is false)
43 = 64  ← (q is true)
Therefore, 53 = 25 or 43 = 64 is a true statement. (‘p or q’ is true)
 
(c)
5 + 7 > 14  ← (p is false)
√9 = 2  ← (q is false)
Therefore, 5 + 7 > 14 or √9 = 2 is a false statement. (‘p or q’ is false)

4.3 Operations on Statements

Posted on by
4.3 Operations on Statements (Part 2)
(B) Truth Values of Compound Statements using ‘And’
 
4. When two statements are combined using ‘and’, a true compound statement is obtained only if both statements are true.
 
5. If one or both statements are false, then the compound statement is false.
 
The truth table:
Let p = statement 1 and q = statement 2.
The truth values for ‘p’ and ‘q’ are as follows:

 
Example 5:
Determine the truth value of the following statements.
(a) 12 × (–3) = –36 and 15 – 7 = 8.
(b) 5 > 3 and –4 < –5.
(c) Hexagons have 5 sides and each of the interior angles is 90o.
 
Solution:
(a)
12 × (–3) = –36 ← (p is true)
15 – 7 = 8 ← (q is true)
Therefore 12 × (–3) = –36 and 15 – 7 = 8 is a true statement. (‘p and q’ is true)
 
(b)
5 > 3 ← (p is true)
–4 < –5 ← (q is false)
Therefore 5 > 3 and –4 < –5 is a false statement. (‘p and q’ is false)

(c)
Hexagons have 5 sides. ← (p is false)
Each of the interior angles of Hexagon is 90o. ← (q is false)
Therefore Hexagons have 5 sides and each of the interior angles is 90o is a false statement. (‘p and q’ is false)

3.4 SPM Practice (Long Questions)

Posted on by

Question 7:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ=P∪Q∪R .
On the diagrams in the answer space, shade set
(a) P ∩ Q,
(b) P ' ∩Q∪R


Solution:
(a) 
P ∩ Q


(b) 
P ' ∩Q∪R



Question 8:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ=P∪Q∪R .
On the diagrams in the answer space, shade set
(a) Q ' ∩R
(b) ( Q∪R )∩ P '



Solution:
(a) 
Q ' ∩R


(b) 
( Q∪R )∩ P '



3.4 SPM Practice (Long Questions)

Posted on by

Question 5:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ=P∪Q∪R
On the diagrams in the answer space, shade
(a) P ∩ Q,
(b) Q∩( P ' ∪R).

Solution:
(a) 
P ∩ Q

(b)
Q∩( P ' ∪R).




Question 6:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ=P∪Q∪R
On the diagrams in the answer space, shade
(a) P ∩ Q,
(b) P∩ (Q∪R) ' .

Solution:
(a)
P ∩ Q


(b)
P∩ (Q∪R) ' .



3.4 SPM Practice (Long Questions)

Posted on by

Question 1:
The Venn diagrams in the answer space shows sets X, Y and Z such that the universal set, ξ = X ∪ Y ∪ Z
On the diagrams in the answer space, shade
( a ) X' ∩ Y , ( b ) ( X ∪ Y' ) ∩ Z


Solution:
(a) 
• X’ ∩ Y means the intersection of the region outside X with the region Y.

 
 
(b)
• Find the region of (X υ Y’) first.
• (X υ Y’) means the union of the region X and the region outside Y.
• The region then intersects with region Z to give the result of (X υ Y’) ∩ Z.





Question 2:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ = P υ Q υ R
On the diagrams in the answer space, shade
(a) Q ∩ R,
(b) (P’ ∩ R) υ Q.

Solution:
(a) 
• Q ∩ R means the intersection of the region Q and the region R.



(b)
• Find the region of (P’ ∩ R) first.
• (P’ ∩ R) means the region that is outside P and is inside R.
• The union of this region with region Q give the result of (P’ ∩ R) υ Q.