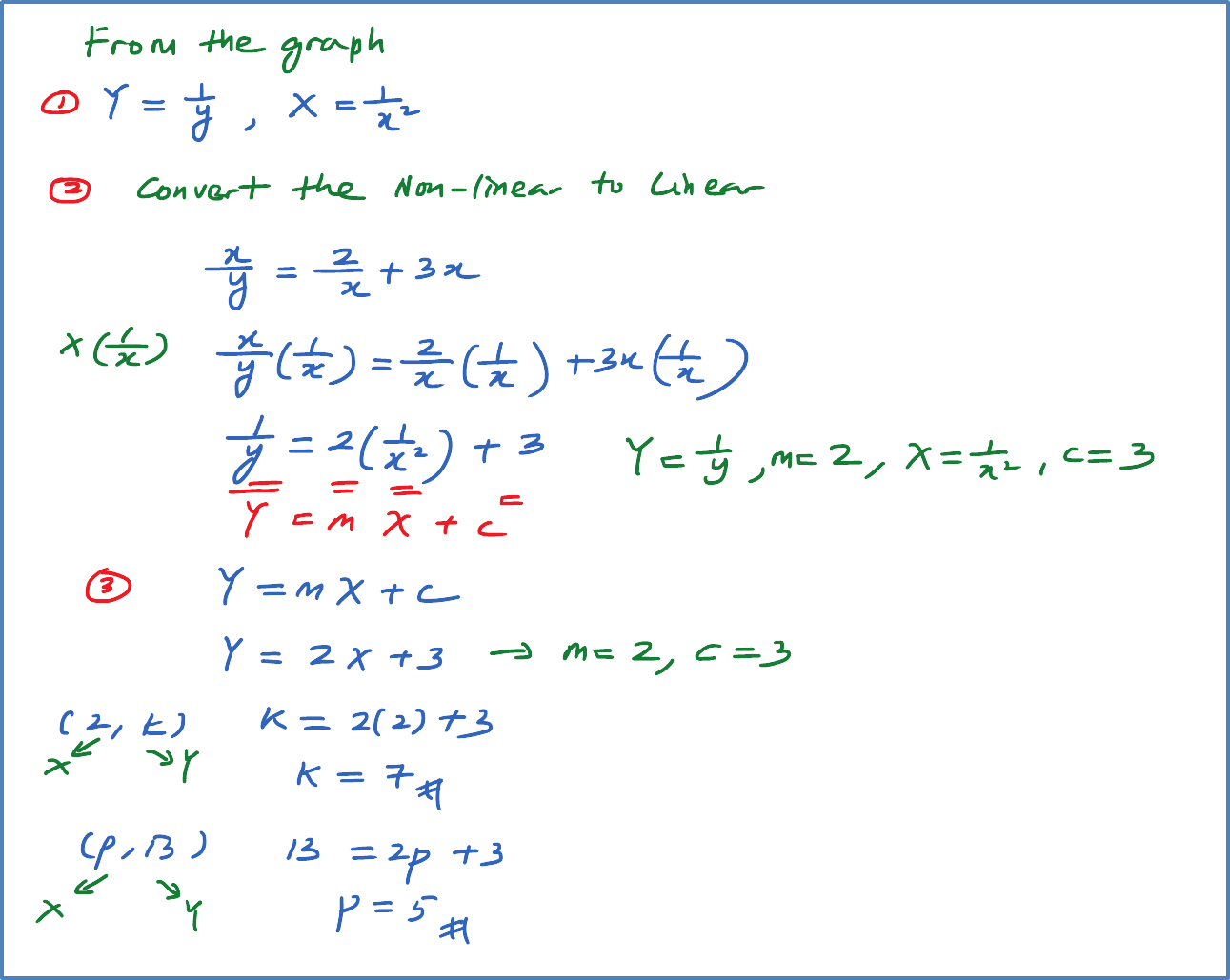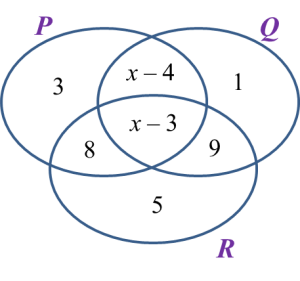
Solution:
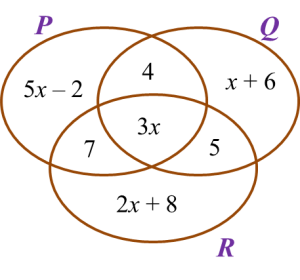
Solution:
8x = 64
x = 8
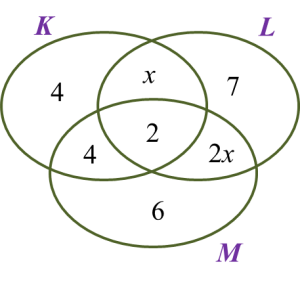
Solution:





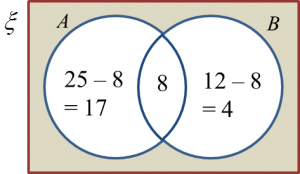

Question 8:
The variables x and y are related by the equation y=p3x, where k is a constant.
Diagram below shows the straight line graph obtained by plotting log10y against x.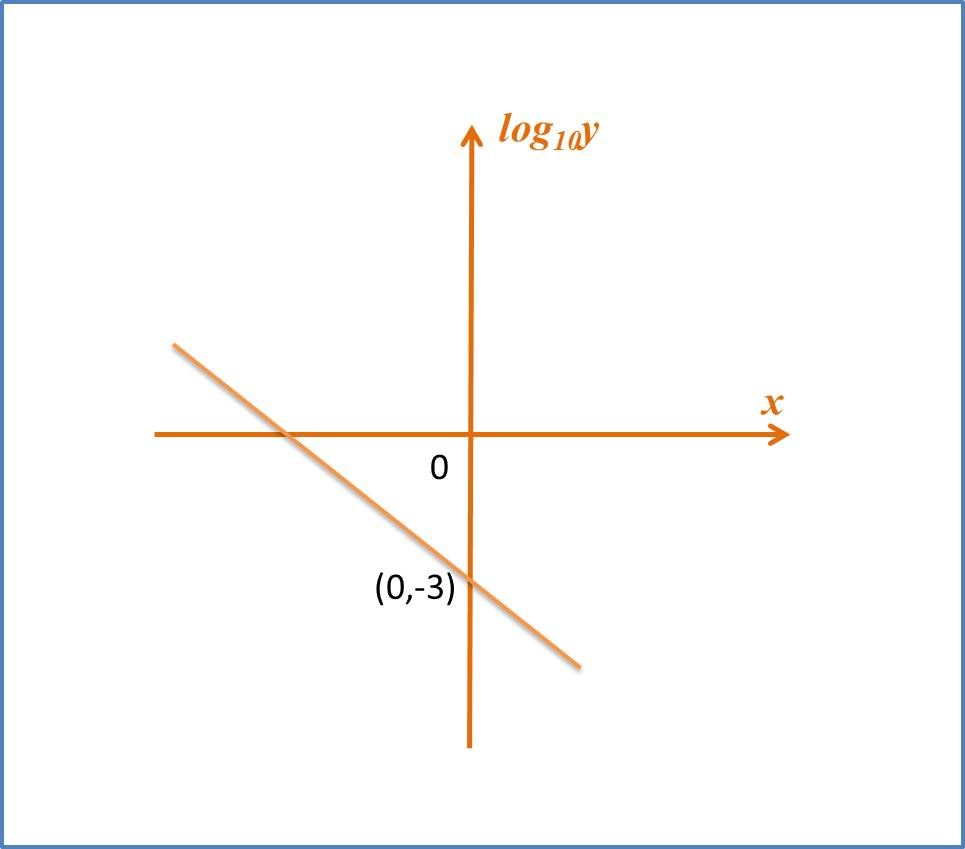
Solution: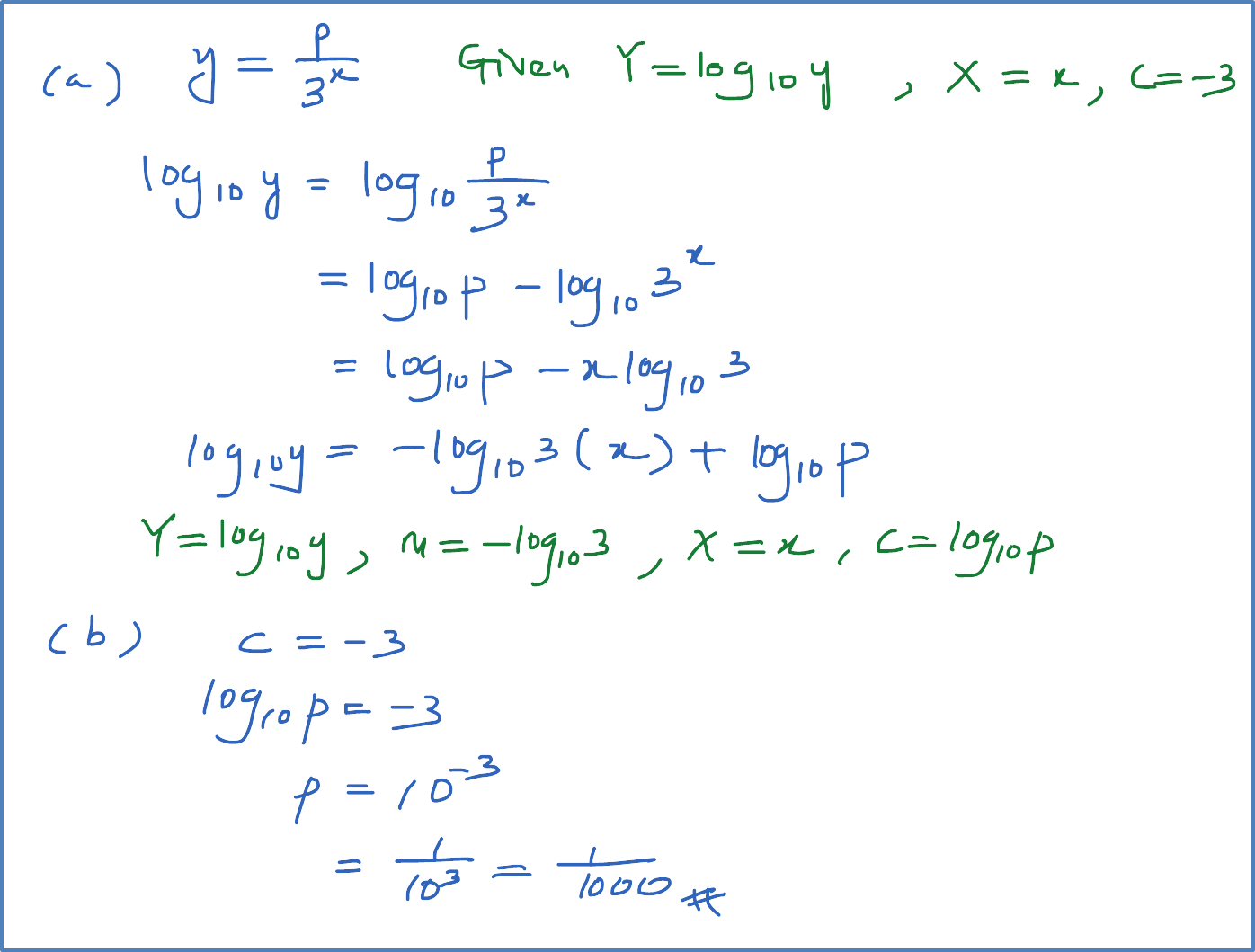
Question 9:
Variable x and y are related by the equation y2=pxq . When the graph lg y against lg x is drawn, the resulting straight line has a gradient of -2 and an vertical intercept of 0.5 . Calculate the value of p and of q.
Solution: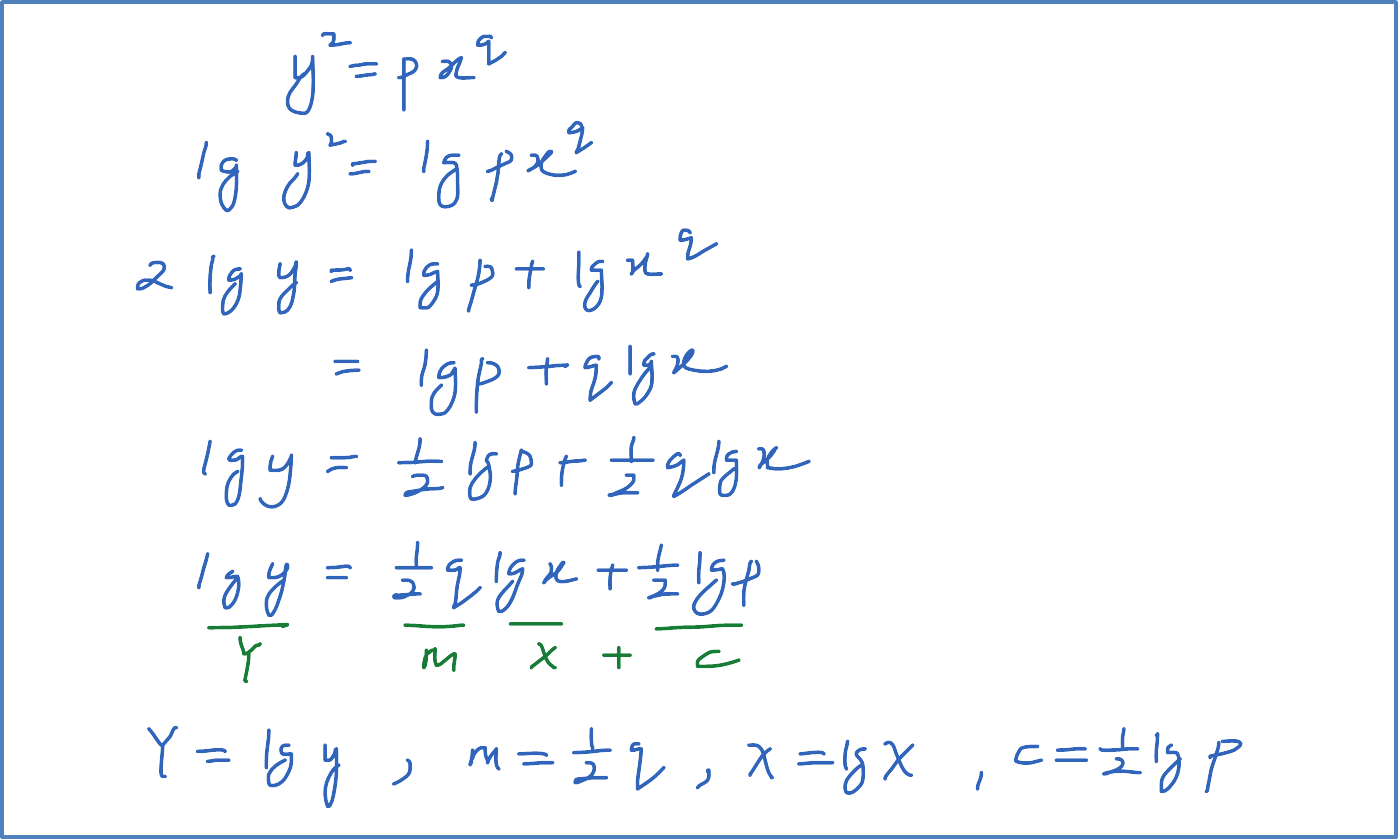
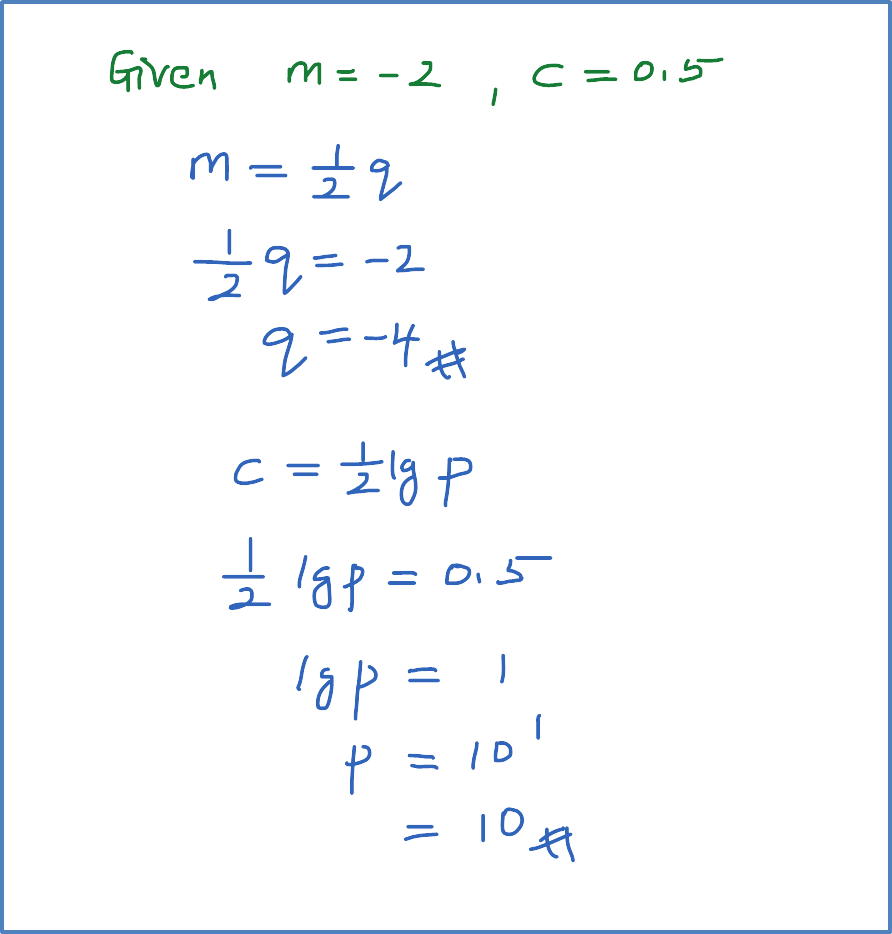
Question 10:
Variable x and y are related by the equation y=cd−x. When the graph y against xy is drawn the resulting line has gradient 0.25 and an intercept on the y-axis of 1.25. Calculate the value of c and of d.
Solution: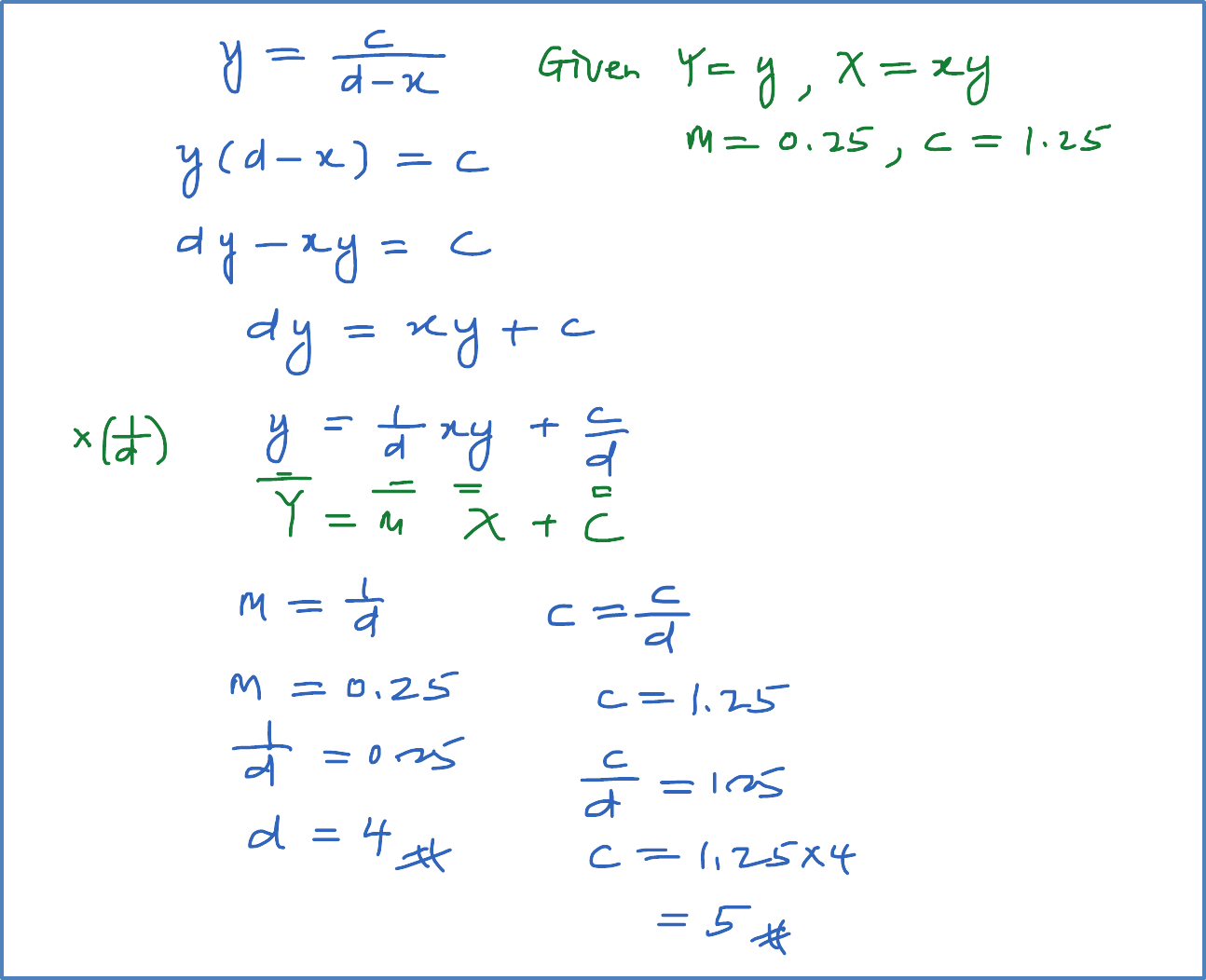
Question 6:
The variables x and y are related by the equation y=px3, where p is a constant. Find the value of p and n.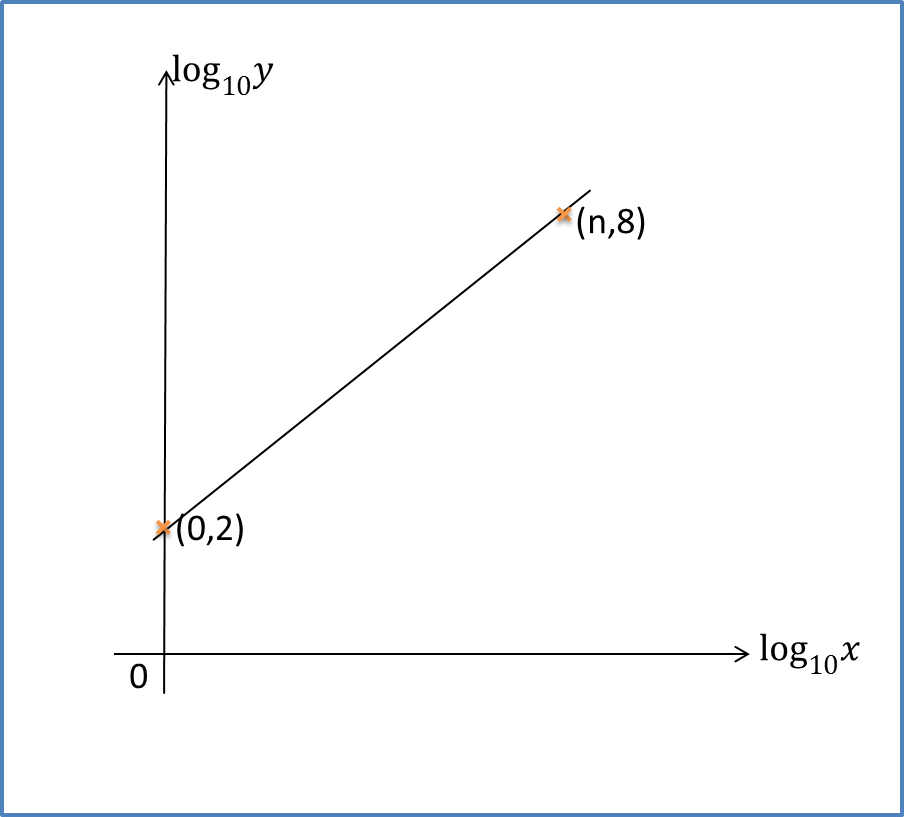
Solution:
Question 7:
Diagram A shows part of the curve y=ax2+bx . Diagram B shows part of the straight line obtained when the equation is reduced to the linear form. Find
(a) the values of a and b,
(b) the values of p and q.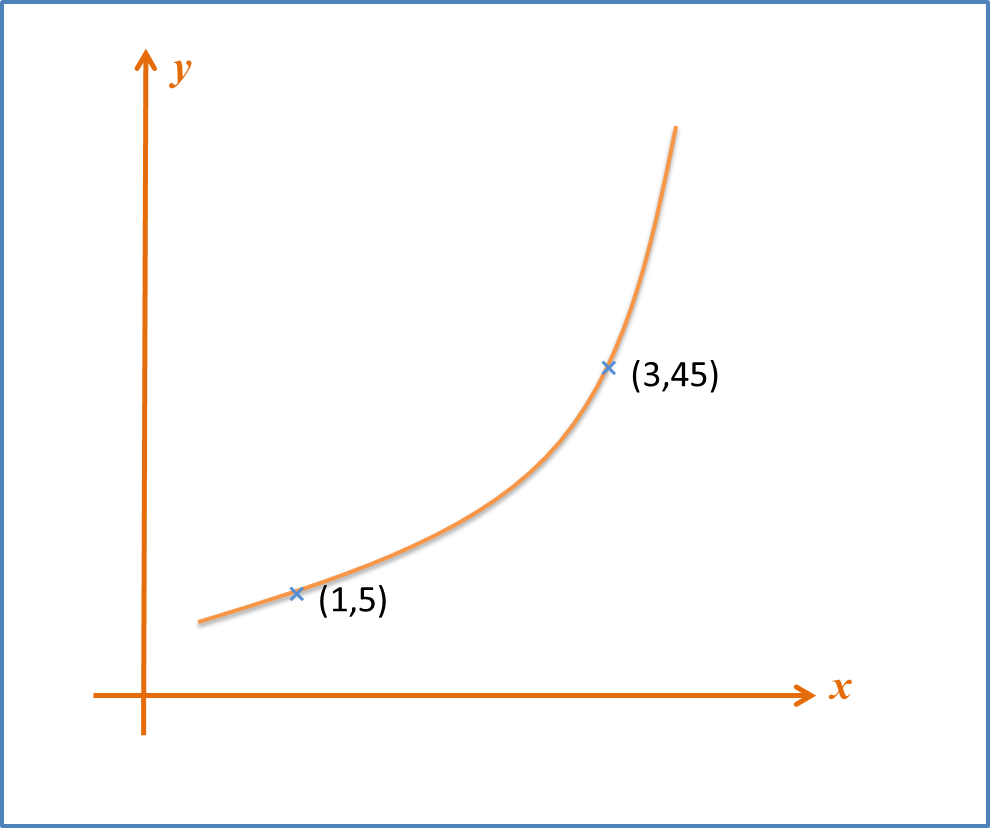
Diagram A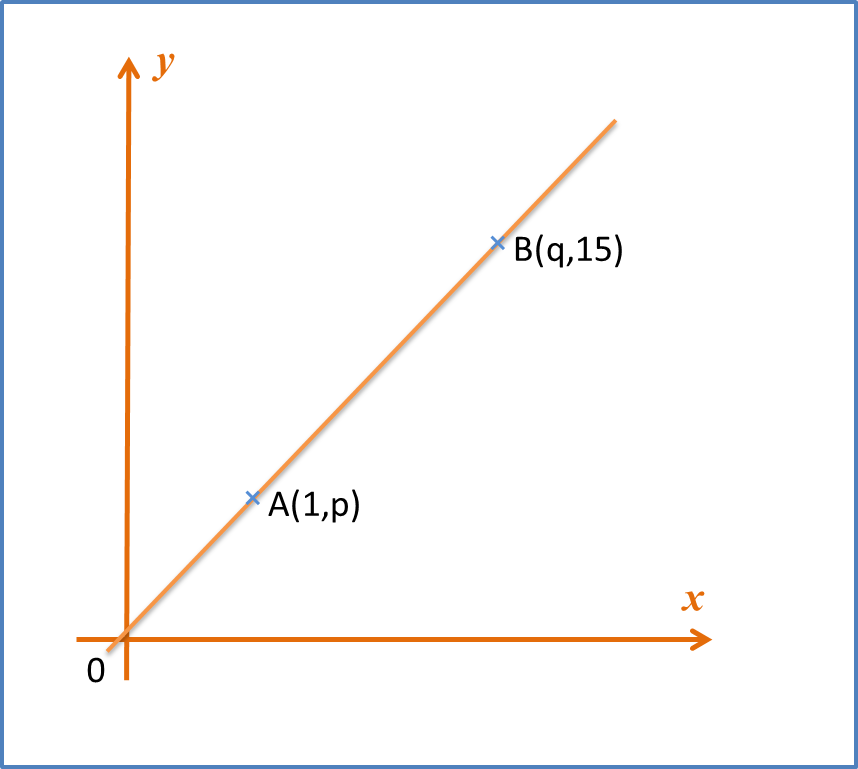
Diagram B
Solution: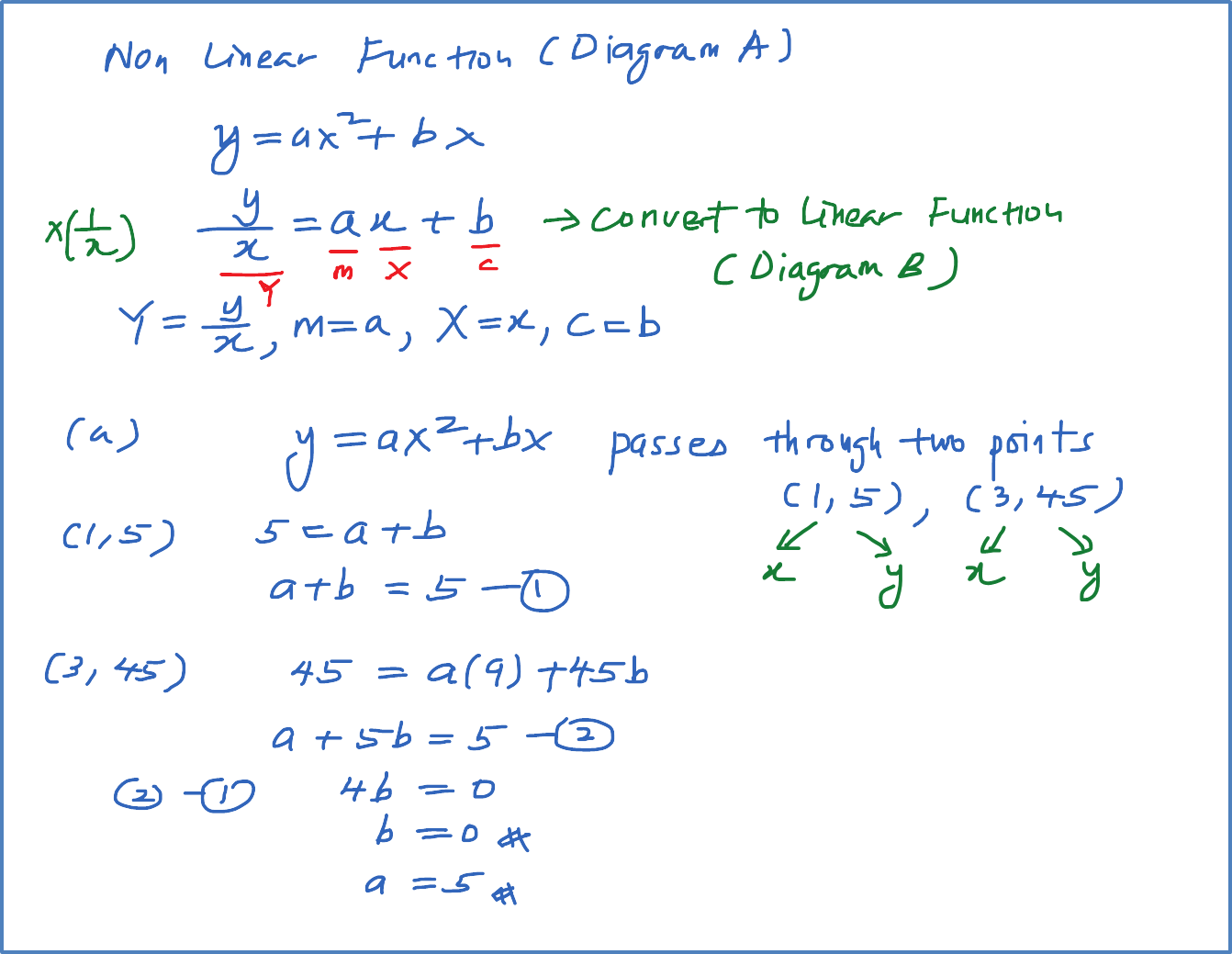
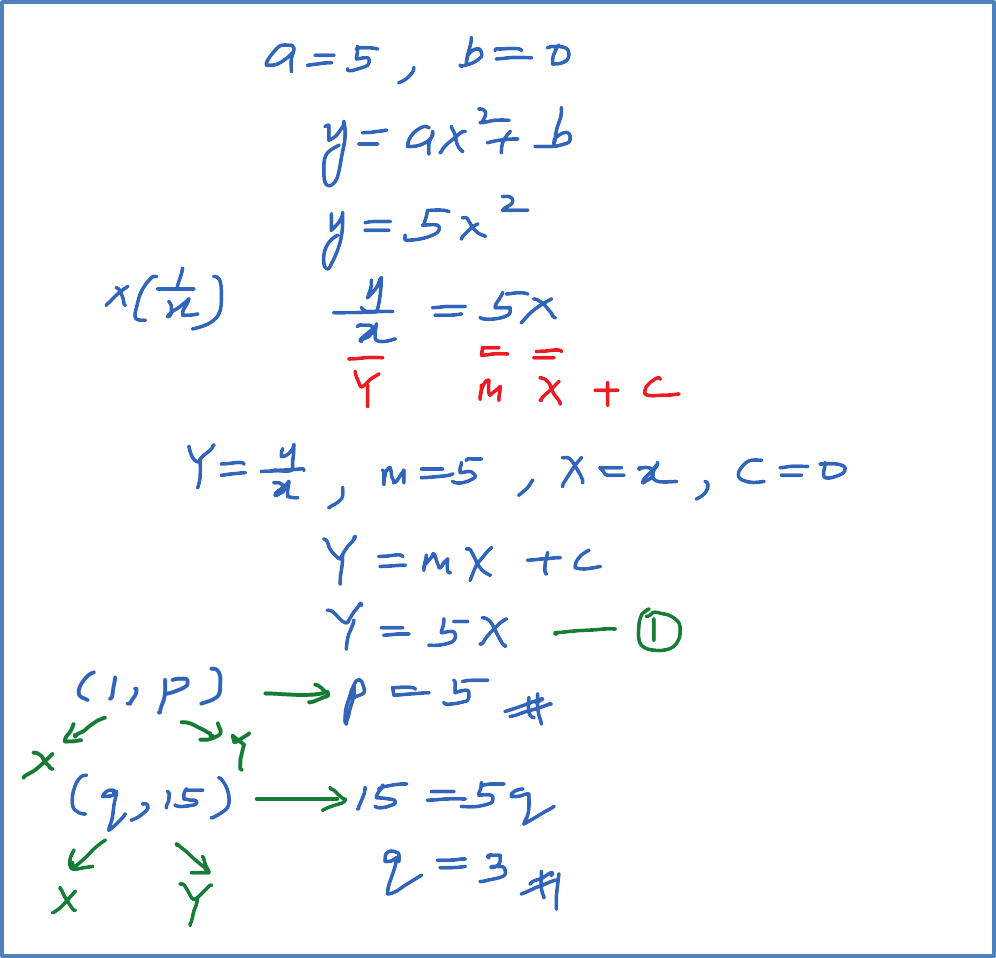
Question 4:
The diagram shows part of the straight line graph obtained by plotting yx against √x.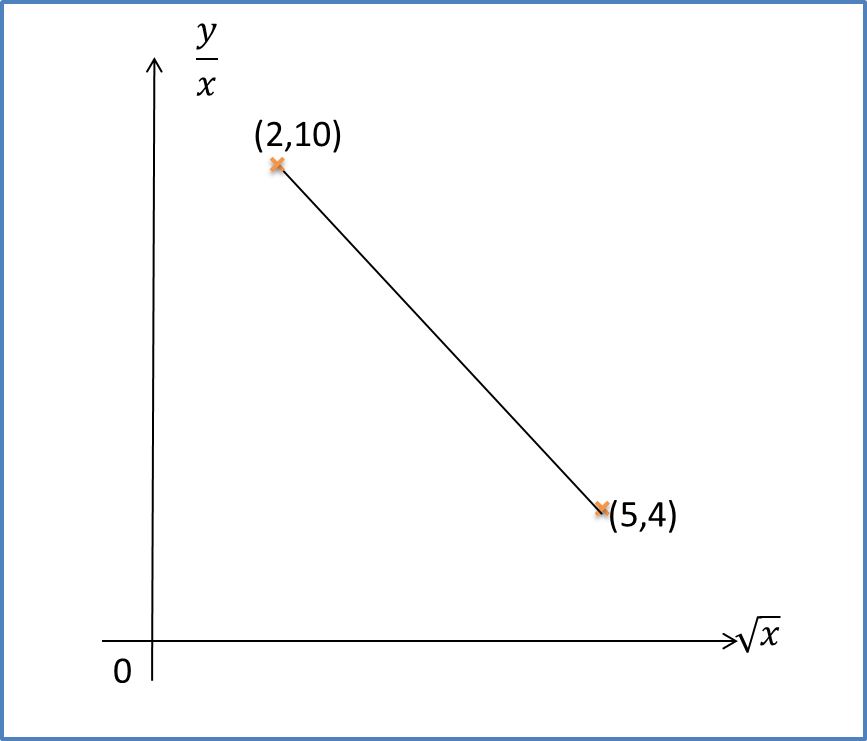
Given its original non-linear equation is y=px+qx32. Calculate the values of p and q.
Solution:
Question 5:
The diagram below shows the graph of the straight line that is related by the equation xy=2x+3x.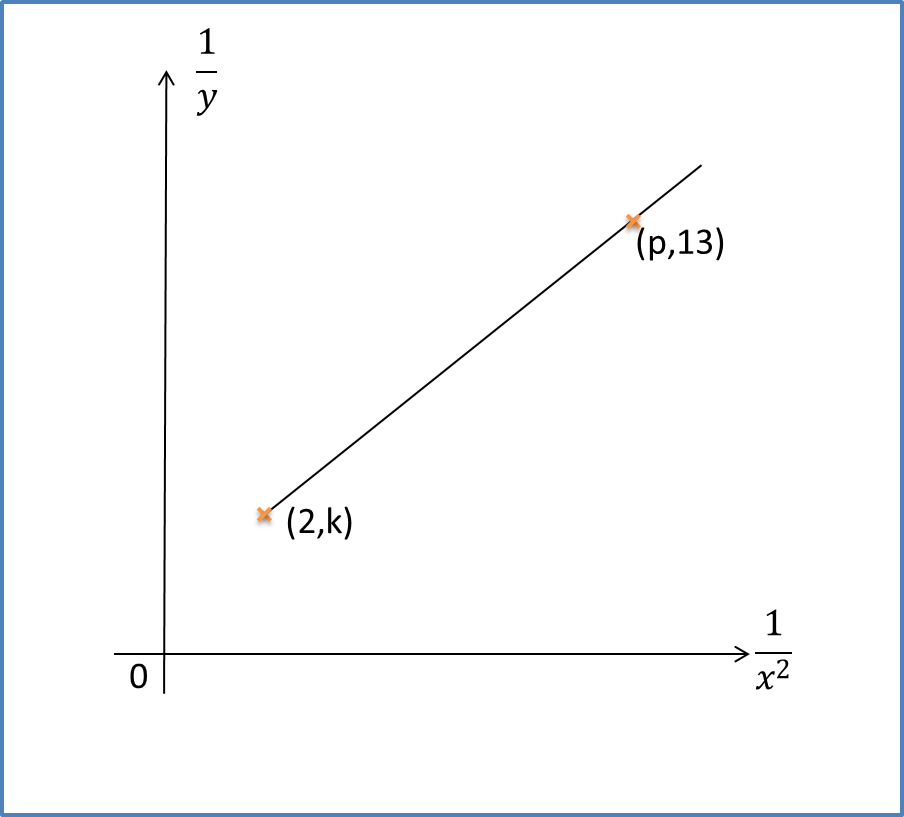
Find the values of p and k.
Solution: