6.6 Sukatan Serakan (Bhg 2)
(B) Median dan Kuartil
1. Kuartil pertama (Q1) ialah suatu nombor dengan keadaan ¼ daripada jumlah data mempunyai nilai yang kurang daripadanya.
2. Median ialah kuartil kedua (nilai yang berada di tengah-tengah data).
3. Kuartil ketiga (Q3) ialah suatu nombor dengan keadaan ¾ daripada jumlah data mempunyai nilai yang kurang daripadanya.
4. Julat antara kuartil adalah beza antara kuartil ketiga dan kuartil pertama.
Julat antara kuartil = kuartil ketiga – kuartil pertama |
Contoh 2:
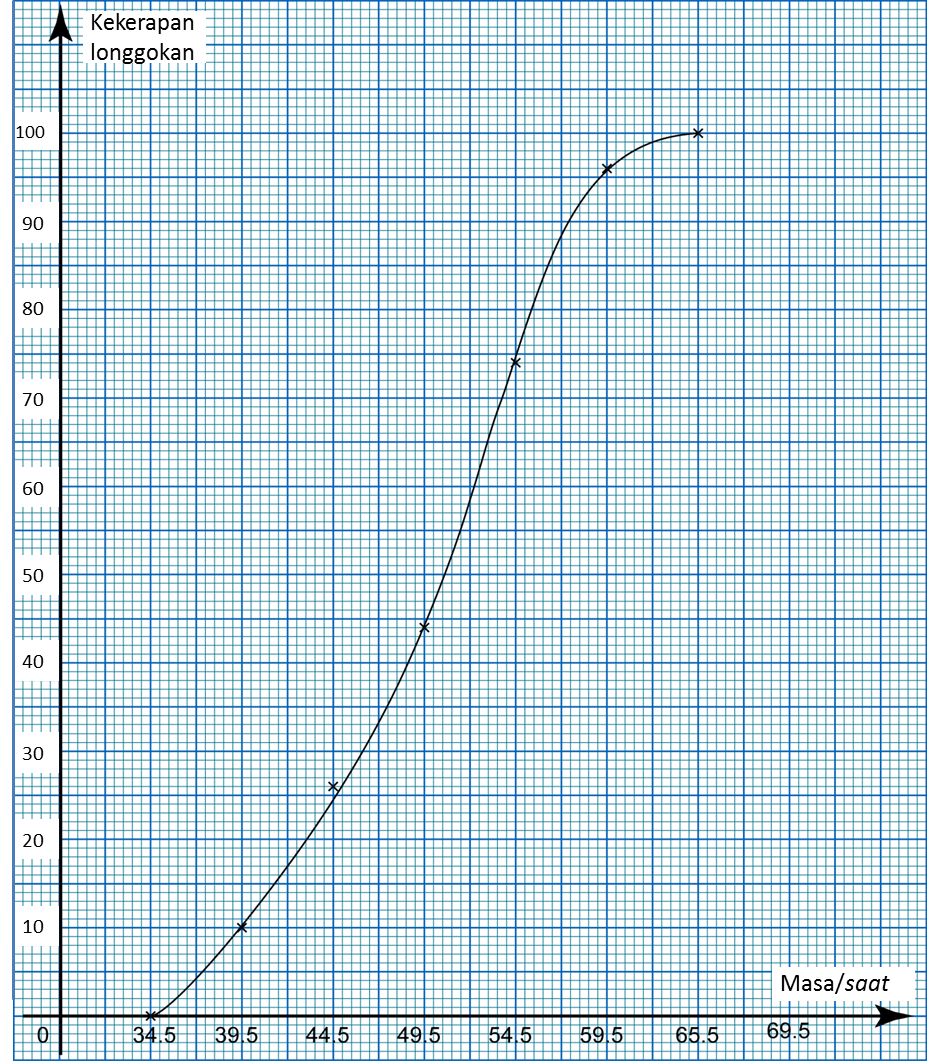
Ogif di atas menunjukkan taburan masa (dalam saat) yang diambil oleh 100 orang pelajar dalam satu pertandingan berenang. Daripada ogif itu, tentukan
(a) median,
(b) kuartil pertama,
(c) kuartil ketiga,
(d) julat antara kuartil bagi masa yang diambil.
Penyelesaian:
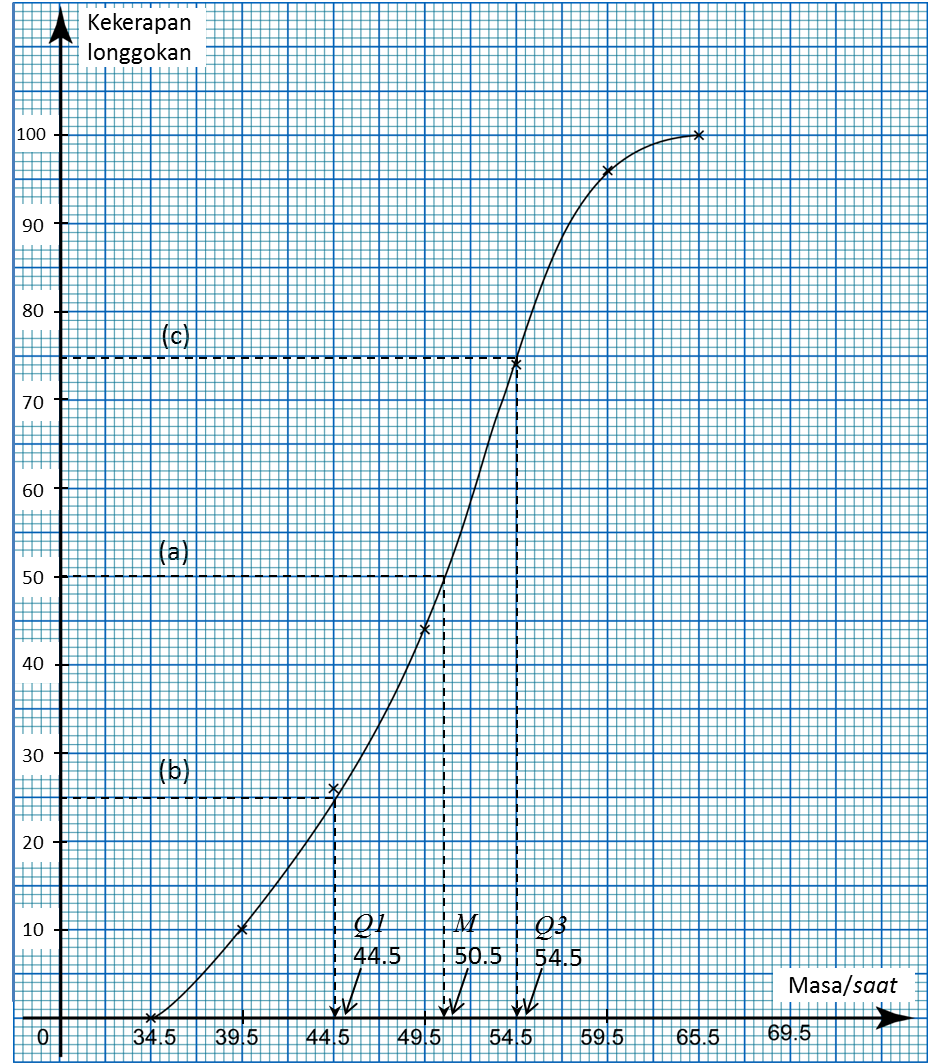
(a) ½ daripada 100 orang pelajar = ½ × 100 = 50
Daripada ogif, median, M = 50.5 saat
(b) ¼ daripada 100 orang pelajar = ¼ × 100 = 25
Daripada ogif, kuartil pertama, Q1= 44.5 saat
(c) ¾ daripada 100 orang pelajar = ¾ × 100 = 75
Daripada ogif, kuartil ketiga, Q3 = 54.5 saat
(d)
Julat antara kuartil
= kuartil ketiga – kuartil pertama
= 54.5 – 44.5
= 10.0 saat
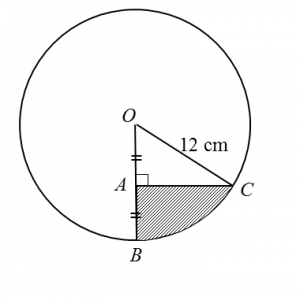 Given that A, B and C are points such that OA = AB and
Given that A, B and C are points such that OA = AB and 
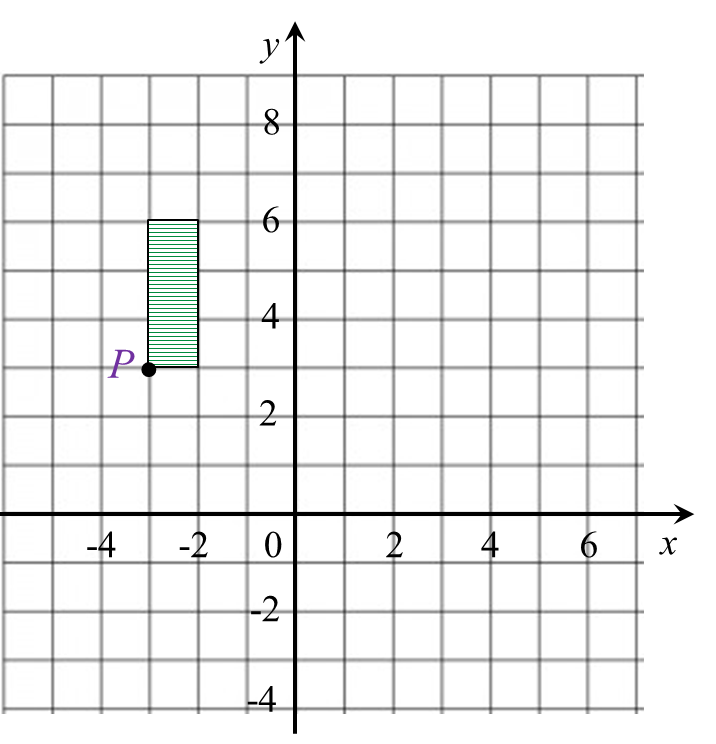 Diagram 9.1
Diagram 9.1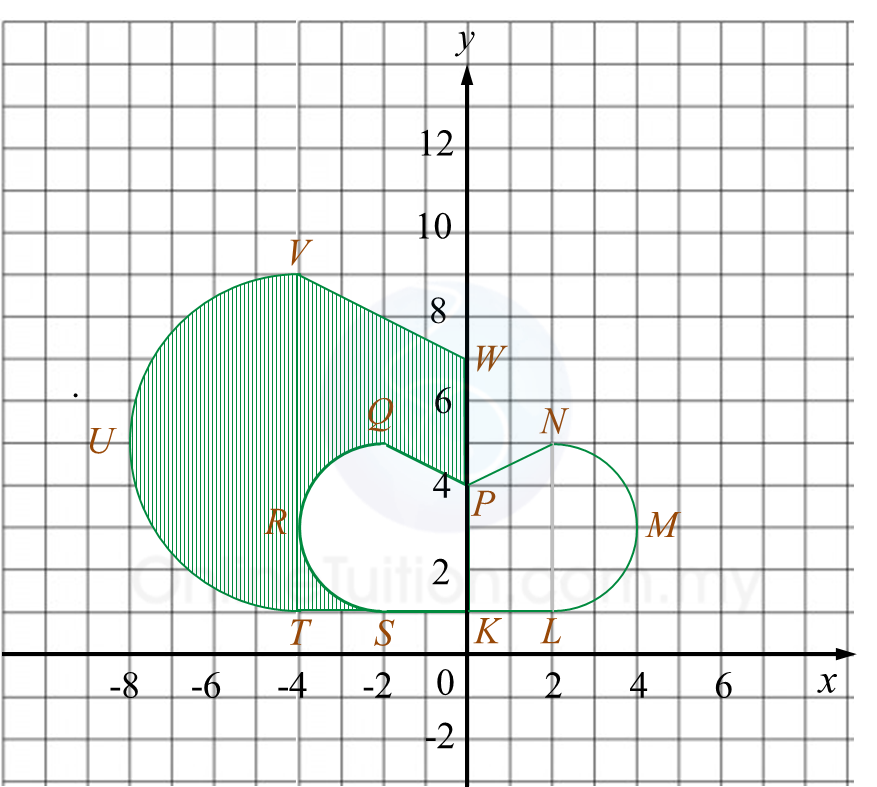 Diagram 9.2
Diagram 9.2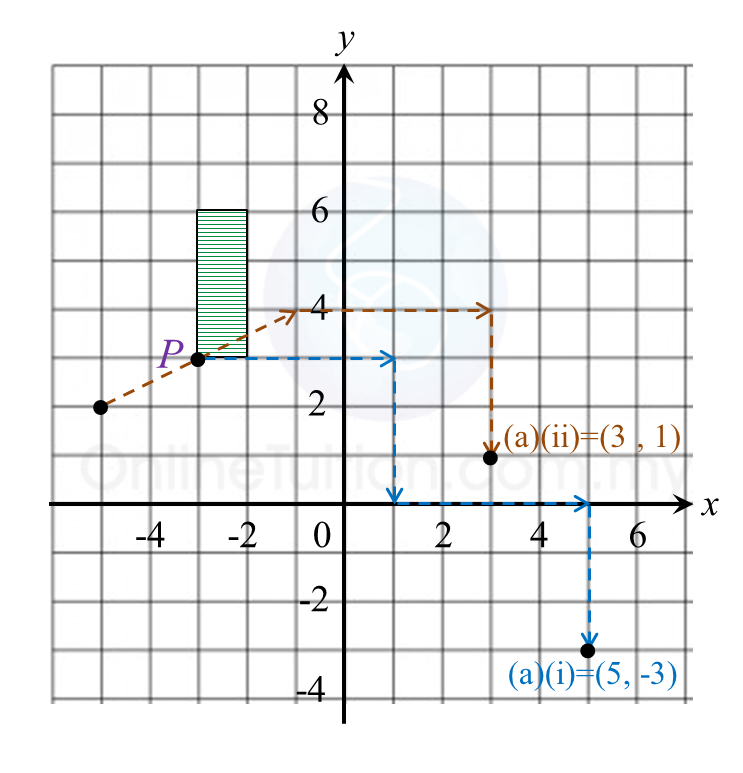
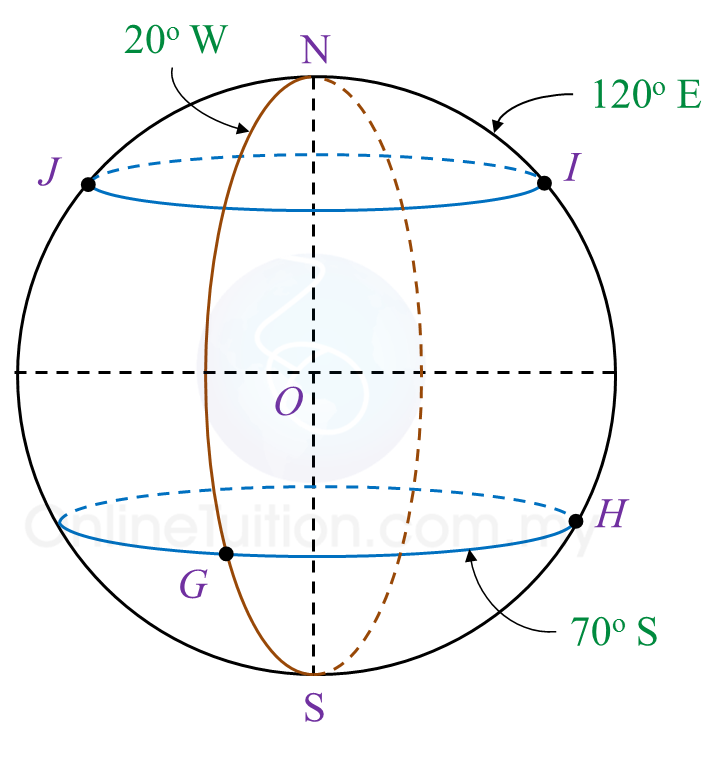 Diagram 8
Diagram 8