Question 1 (10 marks):
Use a graph to answer this question.
Table 1 shows the values of two variables, x and y, obtained from an experiment. A straight line will be obtained when a graph of y2x against 1x is plotted.

(a) Based on Table 1, construct a table for the values of 1x and y2x.
(b) Plot y2x against 1x, using a scale of 2 cm to 0.1 unit on the 1x-axis and 2cm to 2 units on the y2x-axis. Hence, draw the line of best fit.
(c) Using the graph in 1(b)
(i) find the value of y when x = 2.7,
(ii) express y in terms of x.
Solution:
(a)

(b)

(c)(i)
When x=2.7, 1x=0.37From graph,y2x=5.2y22.7=5.2y=3.75
(c)(ii)
Form graph, y-intercept, c = –4gradient, m=16−(−4)0.8−0=25Y=mX+cy2x=25(1x)−4y=√25−4x
Use a graph to answer this question.
Table 1 shows the values of two variables, x and y, obtained from an experiment. A straight line will be obtained when a graph of y2x against 1x is plotted.

(a) Based on Table 1, construct a table for the values of 1x and y2x.
(b) Plot y2x against 1x, using a scale of 2 cm to 0.1 unit on the 1x-axis and 2cm to 2 units on the y2x-axis. Hence, draw the line of best fit.
(c) Using the graph in 1(b)
(i) find the value of y when x = 2.7,
(ii) express y in terms of x.
Solution:
(a)

(b)

(c)(i)
When x=2.7, 1x=0.37From graph,y2x=5.2y22.7=5.2y=3.75
(c)(ii)
Form graph, y-intercept, c = –4gradient, m=16−(−4)0.8−0=25Y=mX+cy2x=25(1x)−4y=√25−4x

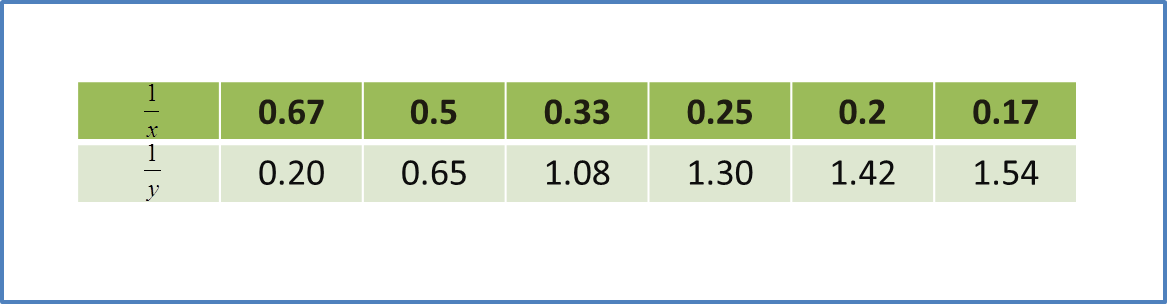
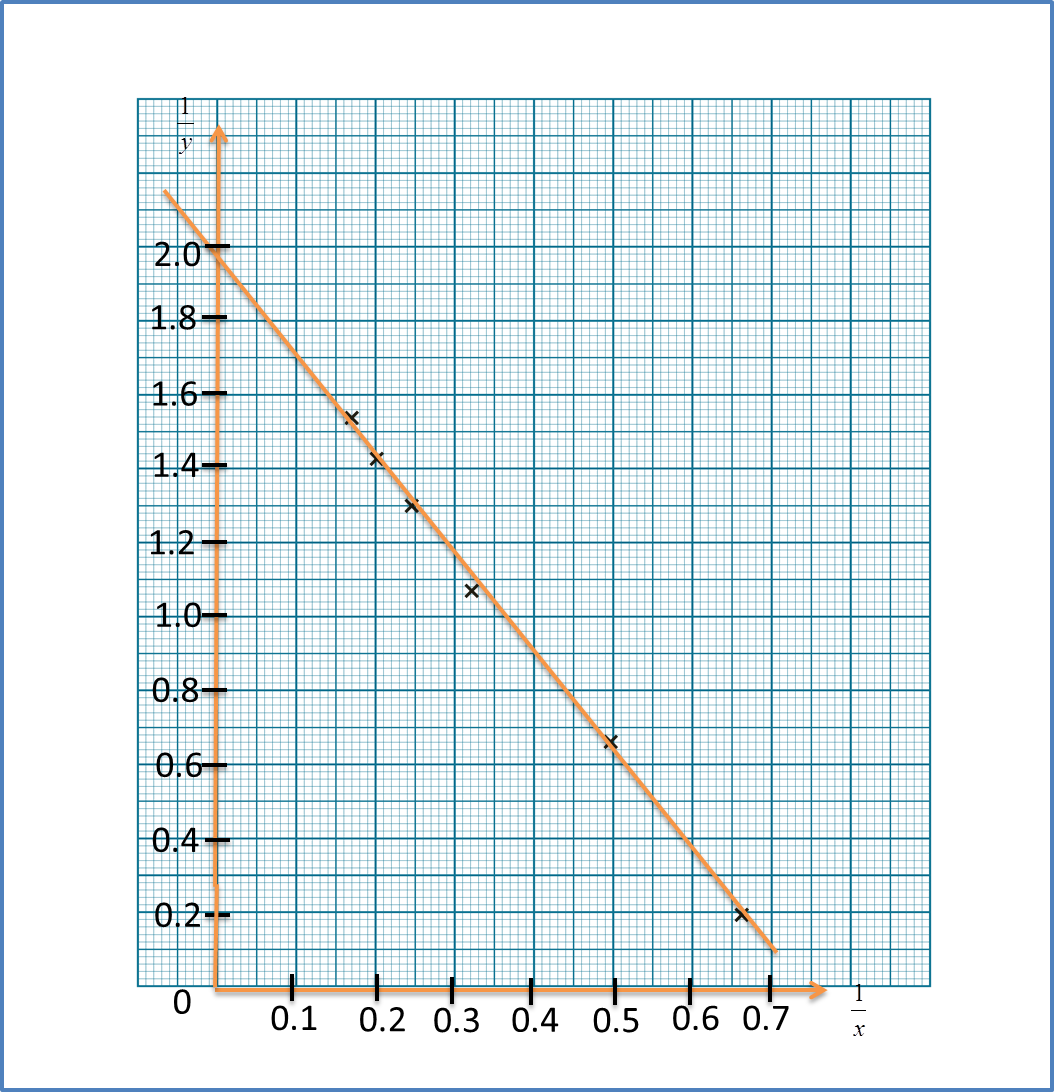
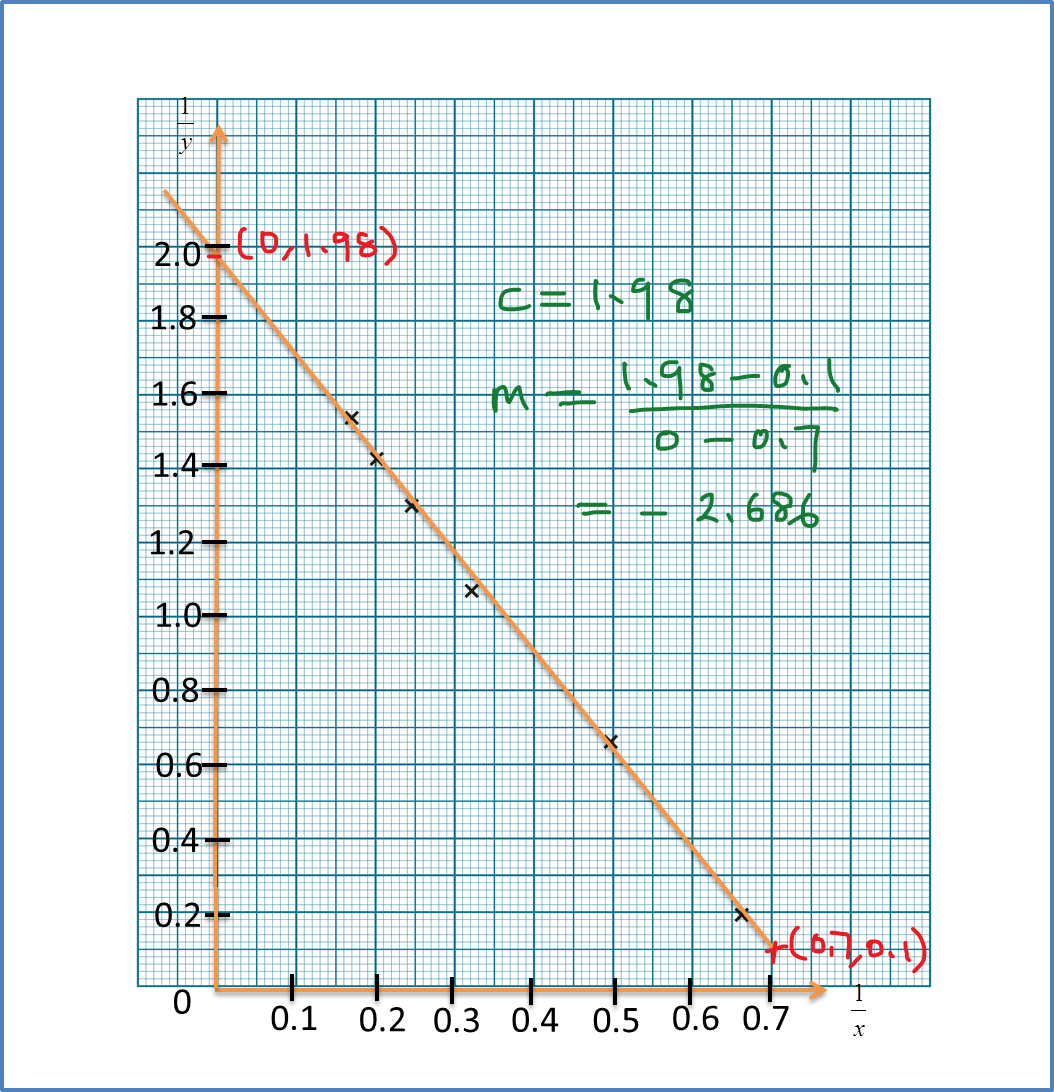




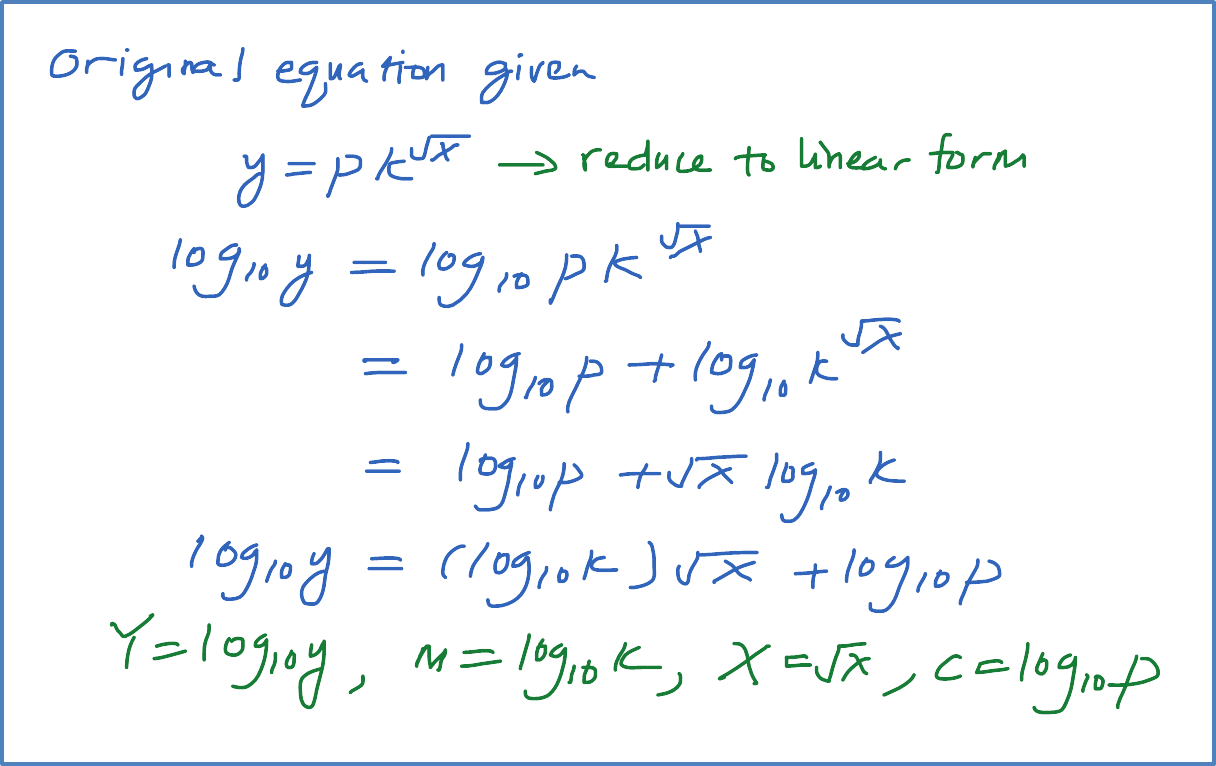
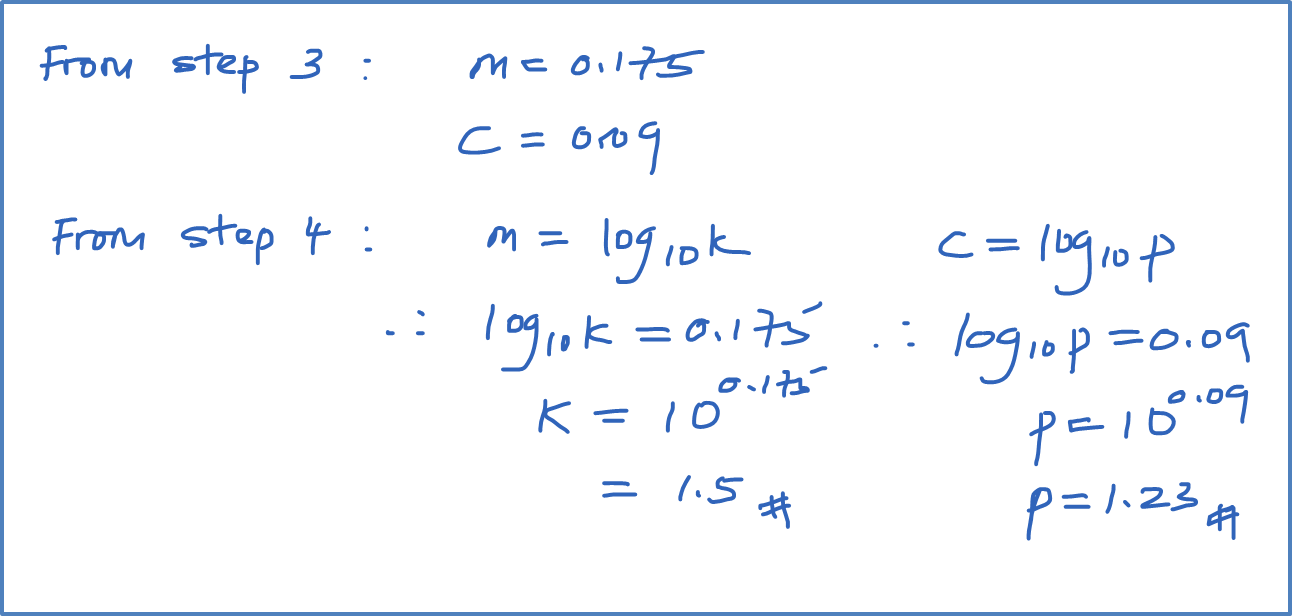
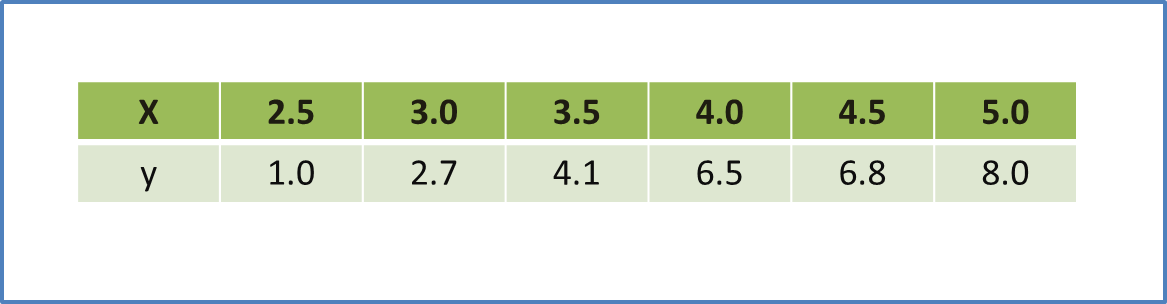


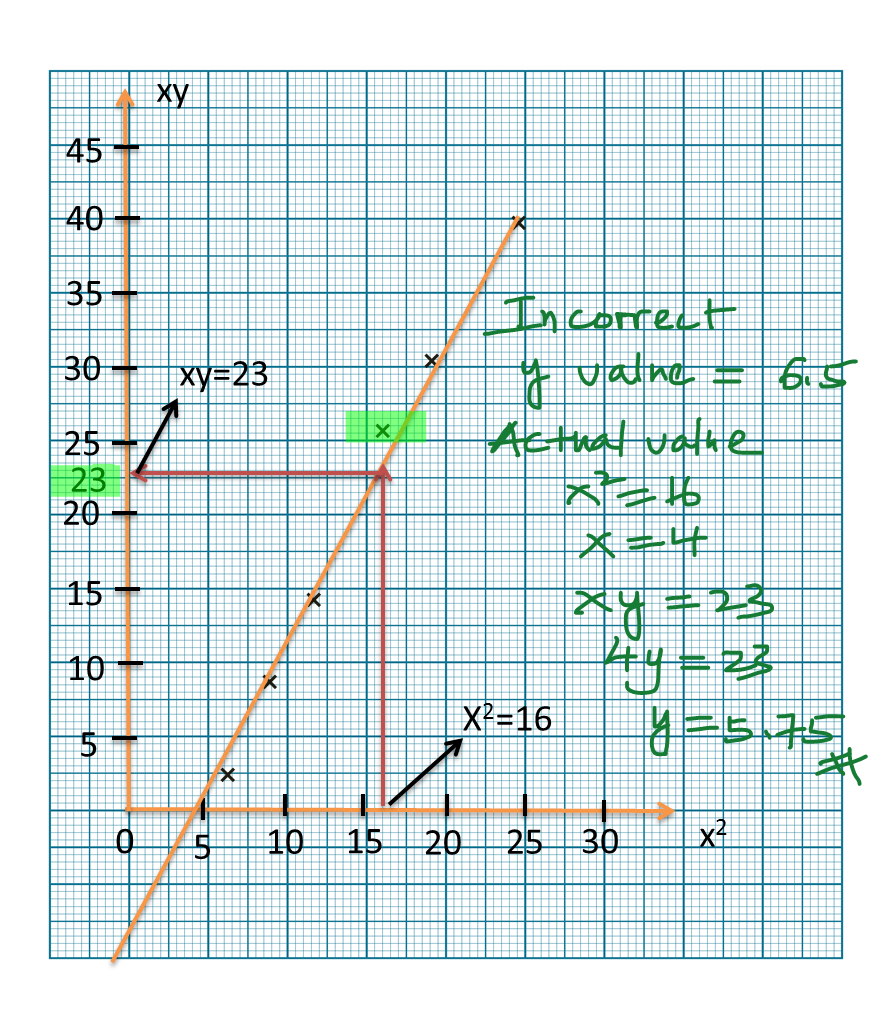
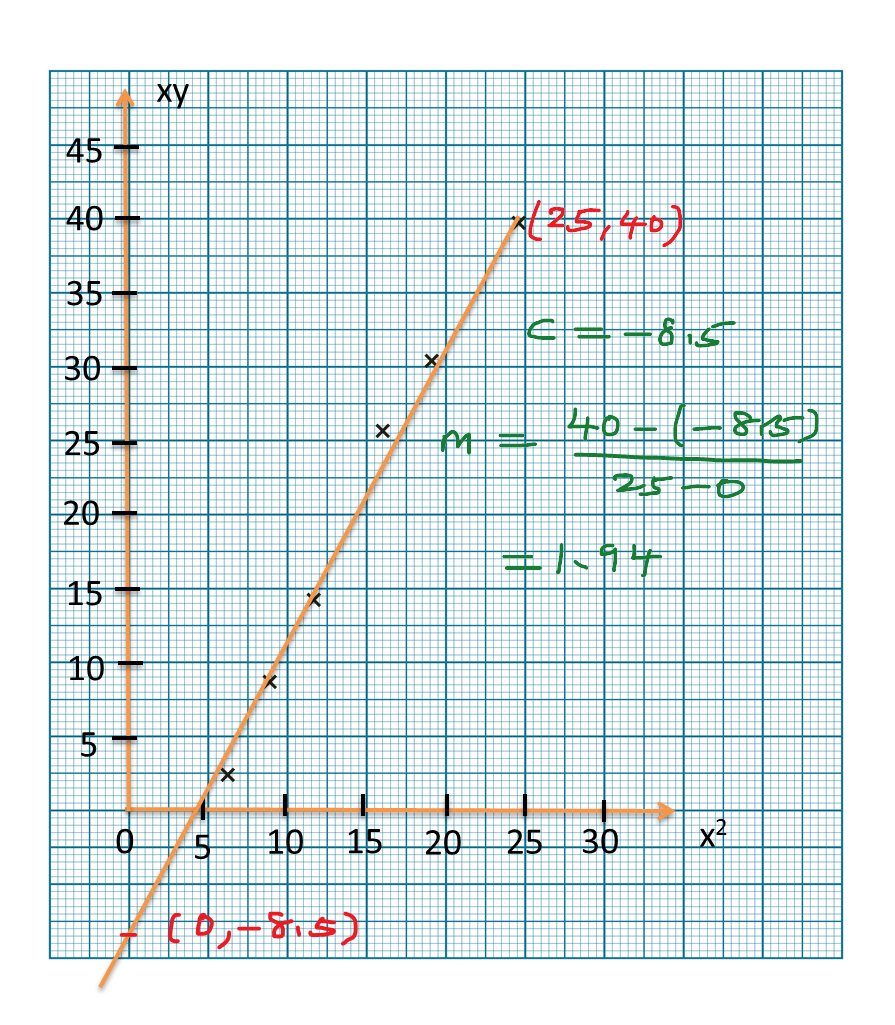

 Diagram 7.1
Diagram 7.1 Diagram 7.2
Diagram 7.2
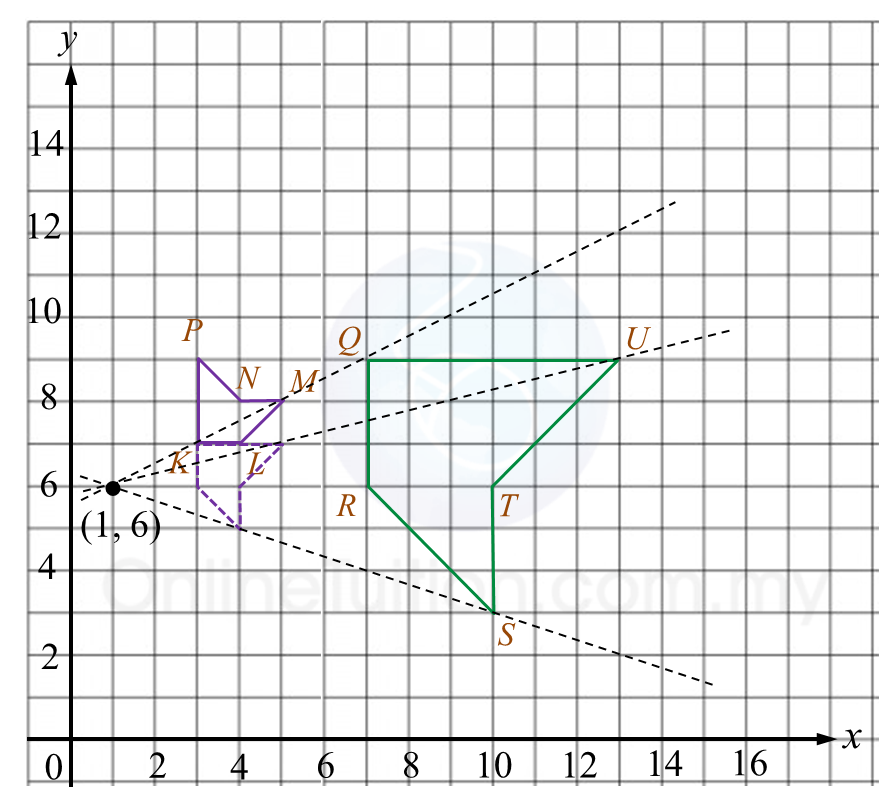

 Diagram 6
Diagram 6
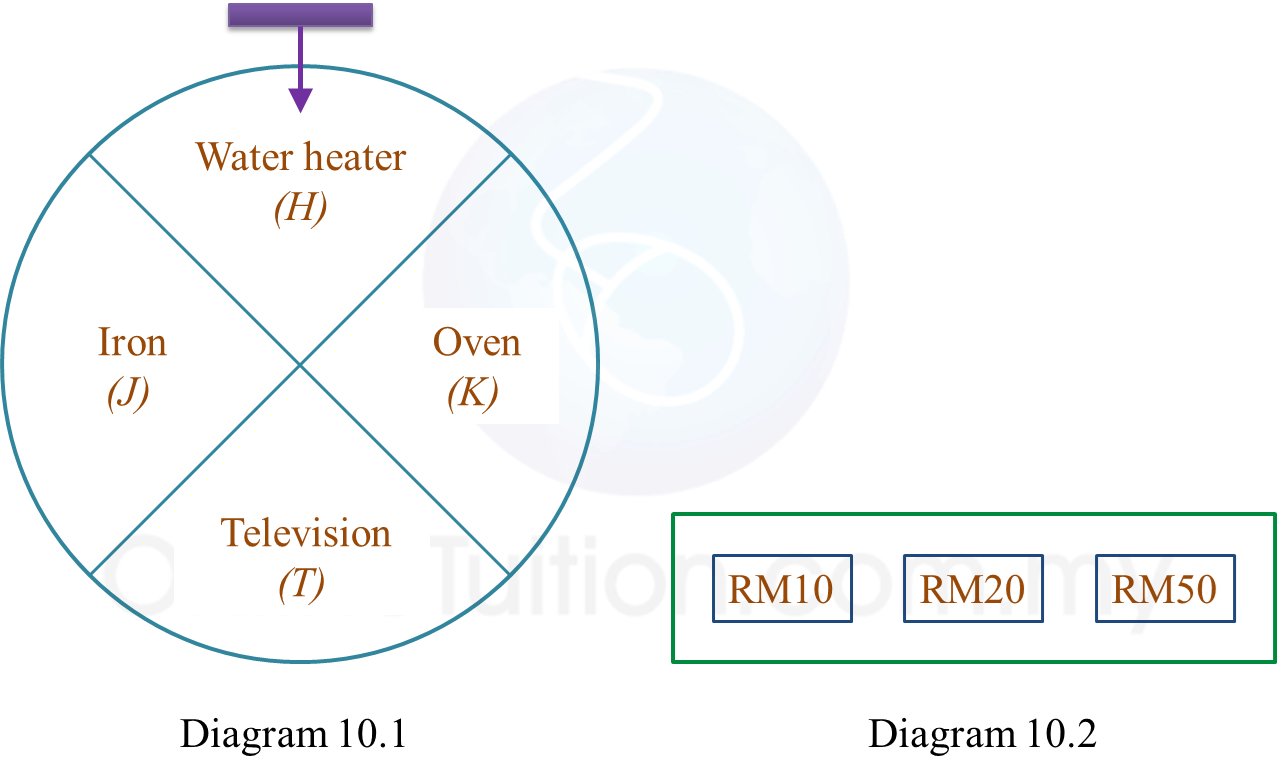




 Diagram 1
Diagram 1
