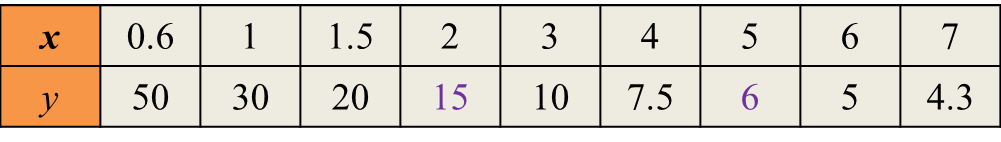Question 11 (5 marks):
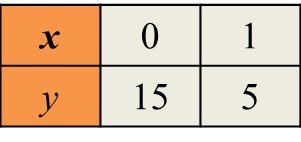
Table 8 shows the information of books purchased by Maslinda.
 Table 8
Table 8
Maslinda purchased x history books and y Science books. The total number of books purchased is 5. The total price of the books purchased is RM17.
(a) Write two linear equations in terms of x and y to represent the above information.
(b) Hence, by using matrix method, calculate the value of x and of y.
Solution:
(a)
x + y = 5
4x + 3y = 17
(b)
(1 14 3)(xy)=( 517) (xy)=11(3)−4(1)( 3 −1−4 1)( 517) (xy)=−1(3(5)+(−1)(17)−4(5)+(1)(17)) (xy)=−1(15−17−20+17) (xy)=−1(−2−3) (xy)=(23)x=2 and y=3
Table 8 shows the information of books purchased by Maslinda.
 Table 8
Table 8Maslinda purchased x history books and y Science books. The total number of books purchased is 5. The total price of the books purchased is RM17.
(a) Write two linear equations in terms of x and y to represent the above information.
(b) Hence, by using matrix method, calculate the value of x and of y.
Solution:
(a)
x + y = 5
4x + 3y = 17
(b)
(1 14 3)(xy)=( 517) (xy)=11(3)−4(1)( 3 −1−4 1)( 517) (xy)=−1(3(5)+(−1)(17)−4(5)+(1)(17)) (xy)=−1(15−17−20+17) (xy)=−1(−2−3) (xy)=(23)x=2 and y=3
Question 12 (6 marks):
Given A=(4 −23 −1), B=m(−1 n−3 4)and I=(1 00 1).
(a) Find the value of m and of n if AB = I.
(b) Write the following simultaneous linear equation as matrix equation:
4x – 2y = 3
3x – y = 2
Hence, by using matrix method, calculate the value of x and of y.
Solution:
(a)
If AB=I, then B=A−1A−1=14(−1)−(−2)(3)(−1 2−3 4)A−1=12(−1 2−3 4)By comparison:B=A−1m(−1 n−3 4)=12(−1 2−3 4)m=12 ; n=2
(b)
4x−2y=33x−y=2(4 −23 −1)(xy)=(32) (xy)=12(−1 2−3 4)(32) (xy)=12((−1)(3)+(2)(2)(−3)(3)+(4)(2)) (xy)=12( 1−1) (xy)=( 12−12)x=12 and y=−12
Given A=(4 −23 −1), B=m(−1 n−3 4)and I=(1 00 1).
(a) Find the value of m and of n if AB = I.
(b) Write the following simultaneous linear equation as matrix equation:
4x – 2y = 3
3x – y = 2
Hence, by using matrix method, calculate the value of x and of y.
Solution:
(a)
If AB=I, then B=A−1A−1=14(−1)−(−2)(3)(−1 2−3 4)A−1=12(−1 2−3 4)By comparison:B=A−1m(−1 n−3 4)=12(−1 2−3 4)m=12 ; n=2
(b)
4x−2y=33x−y=2(4 −23 −1)(xy)=(32) (xy)=12(−1 2−3 4)(32) (xy)=12((−1)(3)+(2)(2)(−3)(3)+(4)(2)) (xy)=12( 1−1) (xy)=( 12−12)x=12 and y=−12
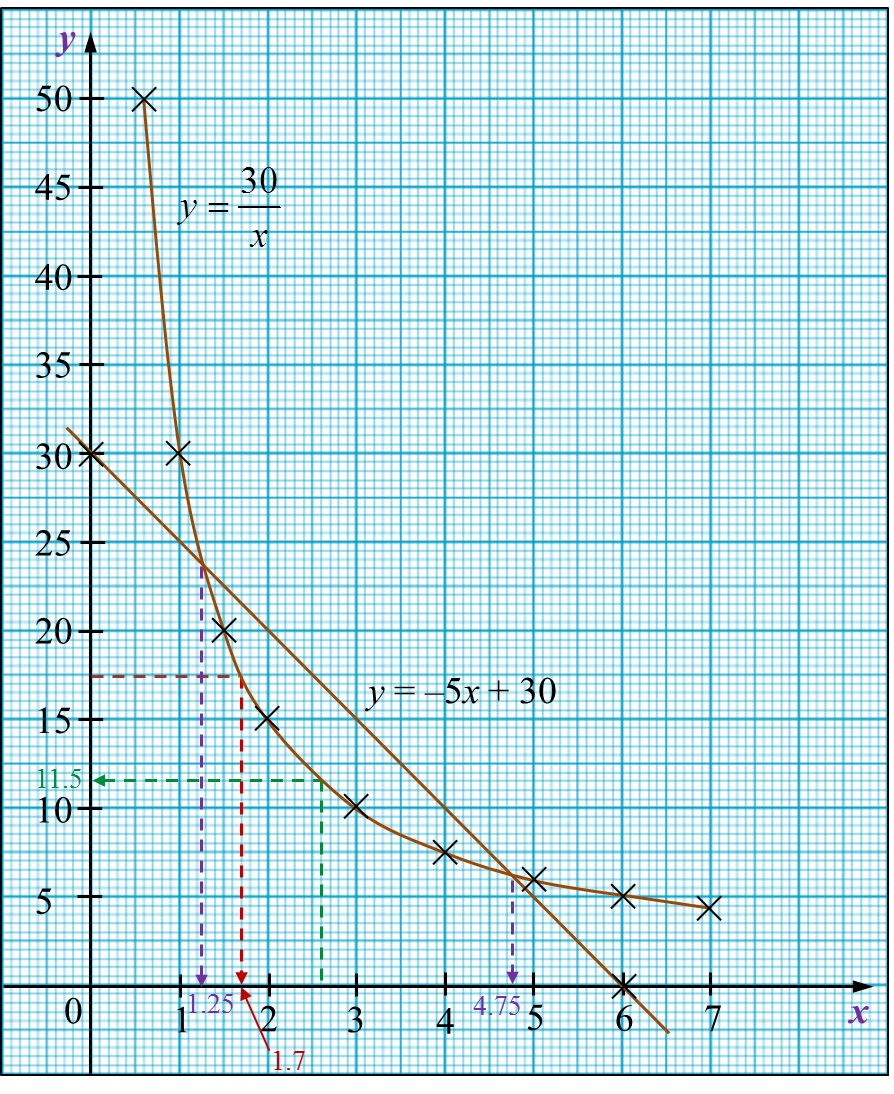
 Diagram 7
Diagram 7 Table 1
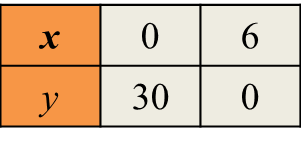
Table 1



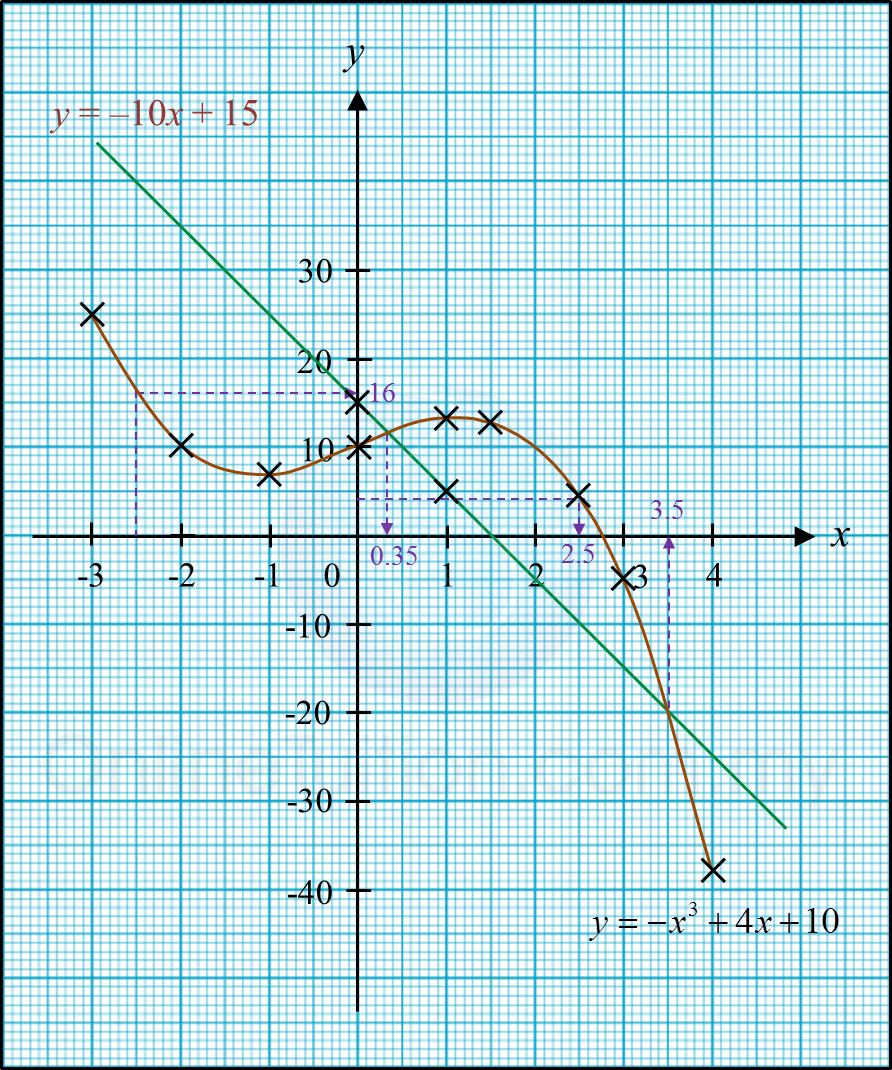
 Diagram 6
Diagram 6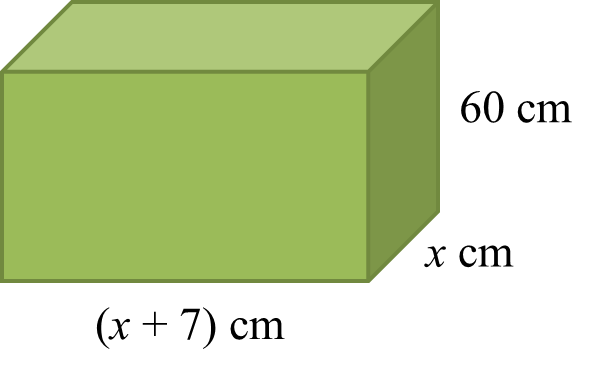

 Table 2
Table 2