Author: Myhometuition
1.2 SPM Practice (Short Questions)
Question 11:
Express each of the following as a number in base two.
(a) 26 + 24 + 1
(b) 25 + 23 + 2 + 20
Solution:
(a)26+24+1=1_×26+0_×25+1_×24+0_×23+0_×22+0_×21+1_×20=10100012
(b)25+23+2+20=1_×25+0_×24+1_×23+0_×22+1_×21+1_×20=1010112
Express each of the following as a number in base two.
(a) 26 + 24 + 1
(b) 25 + 23 + 2 + 20
Solution:
(a)26+24+1=1_×26+0_×25+1_×24+0_×23+0_×22+0_×21+1_×20=10100012
(b)25+23+2+20=1_×25+0_×24+1_×23+0_×22+1_×21+1_×20=1010112
Question 12:
State the value of the digit 2 in the number 324175 , in base ten.
Solution:

Value of the digit 2
= 2 × 53
= 250
State the value of the digit 2 in the number 324175 , in base ten.
Solution:

Value of the digit 2
= 2 × 53
= 250
Question 13:
101102 + 1112 =
Solution:

Alternatively, use a scientific calculator to get the answer directly.
101102 + 1112 =
Solution:

Alternatively, use a scientific calculator to get the answer directly.
Question 14:
1100102 – 1112 =
Solution:
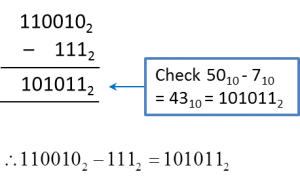
Alternatively, use a scientific calculator to get the answer directly.
1100102 – 1112 =
Solution:

Alternatively, use a scientific calculator to get the answer directly.
1.2 SPM Practice (Short Questions)
Question 8:
Express 110101012 as a number in base eight.
Solution:

Express 110101012 as a number in base eight.
Solution:

Question 9:
Express 100001102 as a number in base eight.
Solution:

Express 100001102 as a number in base eight.
Solution:

Question 10:
Given h8=101112, where h is an integer, find the value of h.
Solution:
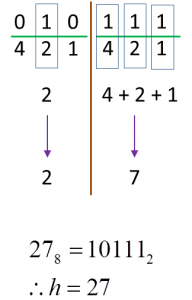
Given h8=101112, where h is an integer, find the value of h.
Solution:

1.2 SPM Practice (Short Questions)
Question 5:
Solution:
What is the value of the digit 3, in base ten, in the number 43155?
Identify the place value of each digit in the number first.
4 |
3 |
1 |
5 |
|
Place Value |
53 |
52 |
51 |
50 |
Value of the digit 3
= 3 × 52
= 75Question 6:
Solution:
Express 5(52 + 2) as a number in base 5.
Step 1: Expand 5(52 + 2) first.
Step 2: write 5(52 + 2) in expanded notation for base 5.
5(52 + 2)
= 53 + 2 × 5
= 1 × 53 + 0 × 52 + 2 × 51+ 0 × 50
= 10205
53 |
52 |
51 |
50 |
1 |
0 |
2 |
05 |
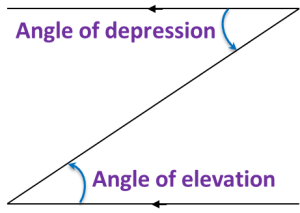
10.1 Angle of Elevation and Angle of Depression (Part 2)
3. The angle of elevation or angle of depression is always measured from the horizontal line.

Example 3:
Diagram below shows two vertical poles JK and NL on a horizontal plane. M is a point on NL such that JK = ML.
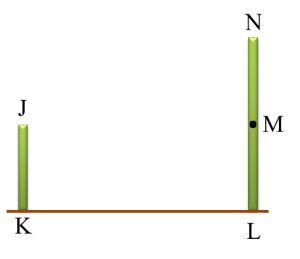

The angle of depression of point J from point N is
Solution:
The angle of depression of point J from N is the angle between line JN and the horizontal line through N.
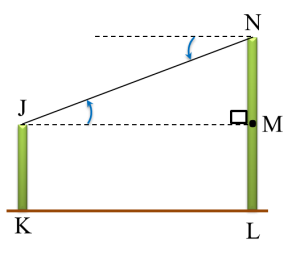

Angle of depression of J from N
= angle of elevation of N from J
=∠NJM
=∠NJM
SPM Practice (Short Questions)
8.4 Circles, SPM Practice (Short Questions)
Question 9:


In figure above, ABC is a tangent to the circle centre O at B. AED is a straight line.
Find the value of y.
Solution:
∠ABO = 90o
∠BOE = 2 × 40o = 80o
In quadrilateral AEOB,
∠AEO = 360o – ∠ABO – ∠BOE – 35o
= 360o – 90o – 80o – 35o = 155o
yo+ ∠AEO = 180o
yo+ 155o = 180o
yo = 180o – 155o
y o = 25
Question 10:

In figure above, ABC is a tangent to the circle centre O, at point B.
The value of x is
Solution:
∠OBC = 90o
∠BOD = 2 × 50o = 100o
In quadrilateral BODC,
xo = 360o – ∠BOD – ∠OBC – 120o
= 360o – 100o – 90o – 120o
= 50
8.3 Common Tangents (Part 3)
3. Do not intersect
(a) Circles of the same size
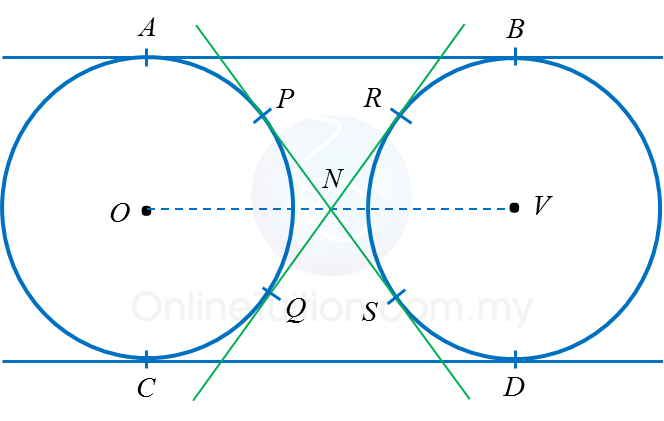

Number of common tangents |
Properties of common tangents |
Four common tangents:
AB, CD, PS and RQ |
AB = CD = OV
PS = RQ
AB // OV // CD |
(b) Circles of different sizes
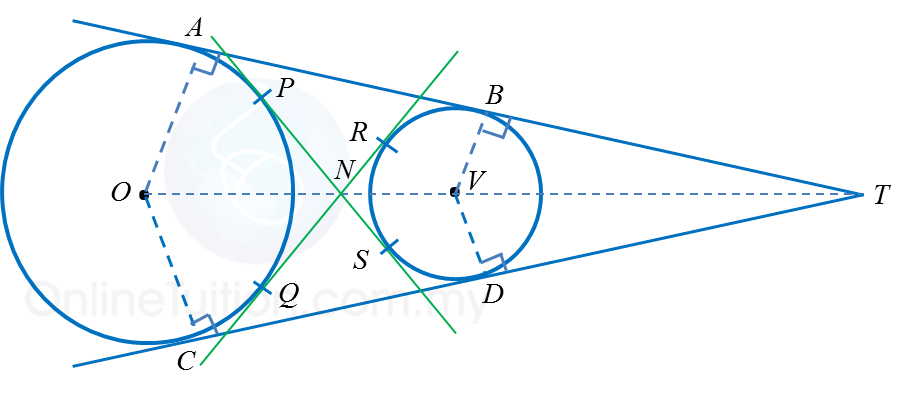

Number of common tangents |
Properties of common tangents |
Four common tangents:
AB, CD, PS and RQ |
AB = CD
BT = DT
PS = RQ
OA // VB
OC // VD |
8.3 Common Tangents (Part 2)
2. Intersect at one point
(a) Circles of the same size
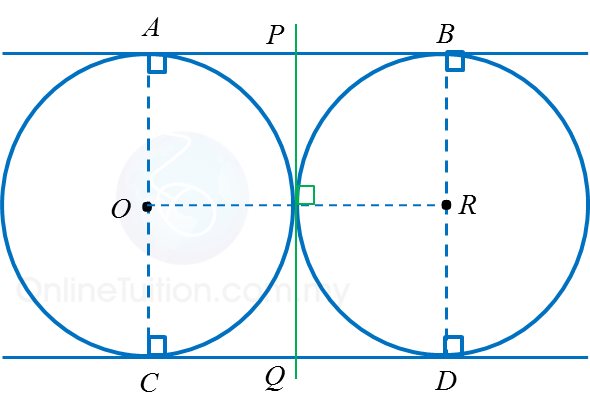

Number of common tangents |
Properties of common tangents |
Three common tangents:
AB, CD and PQ |
AC = PQ = BD
AB = OR = CD
AB // OR // CD
AC // PQ // BD
PQ perpendicular to OR |
(b) Circles of different sizes
(i) External contact
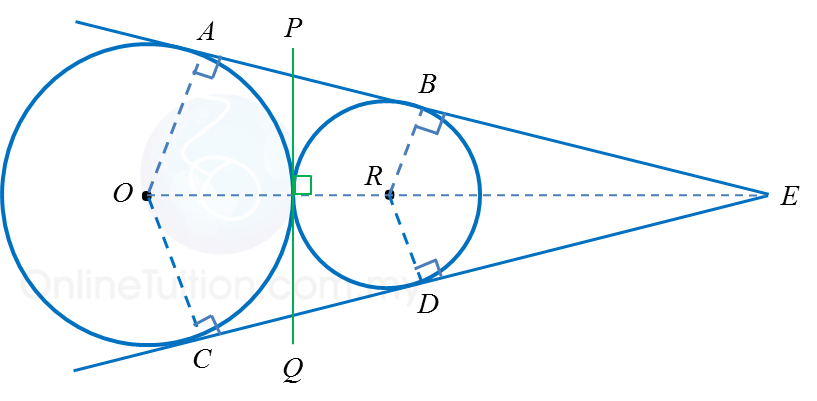
Number of common tangents |
Properties of common tangents |
Three common tangents:
ABE, CDE and PQ |
AB = CD
BE = DE
OA // RB
OC // RD
PQ perpendicular to ORE |
(ii) Internal contact
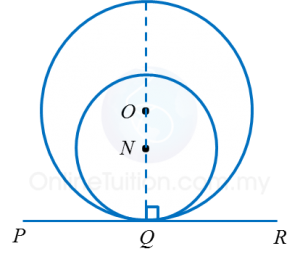
Number of common tangents |
Properties of common tangents |
One common tangent: PQR |
ONQ perpendicular to PR |
8.2 Angle between Tangent and Chord (Example 3 & 4)
Example 3:
In the diagram, PQR is a tangent to the circle QSTU at Q.
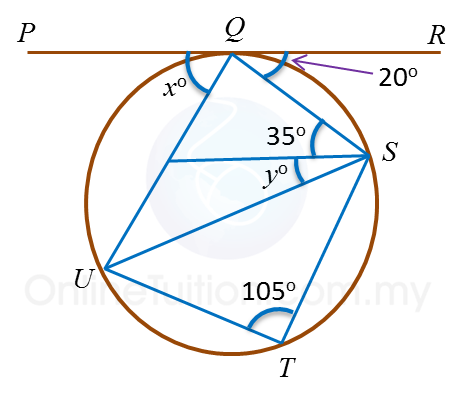

Find the values of
(a) x (b) y
Solution:
(a)
∠UTS + ∠UQS = 180o ←(opposite angle in cyclic quadrilateral QSTU)
105o + ∠ UQS = 180o
∠ UQS = 75o
x+ 75o + 20o = 180o←(the sum of angles on a straight line PQR = 180o)
x+ 95o = 180o
x = 85o
(b)
∠ PQU = ∠ QSU ← (angle in alternate segment)
85o = 35o + y
y = 50o Example 4:
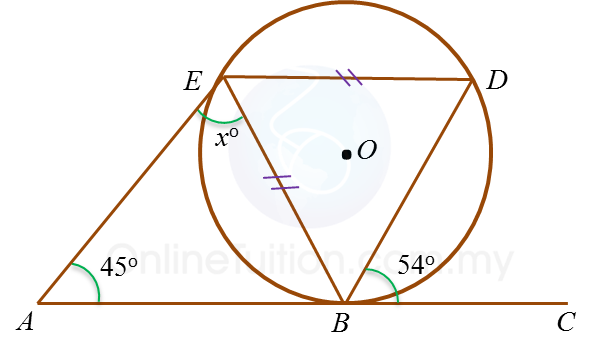

In the diagram, ABC is a tangent to the circle BDE with centre O, at B.
Find the value of x.
Solution:
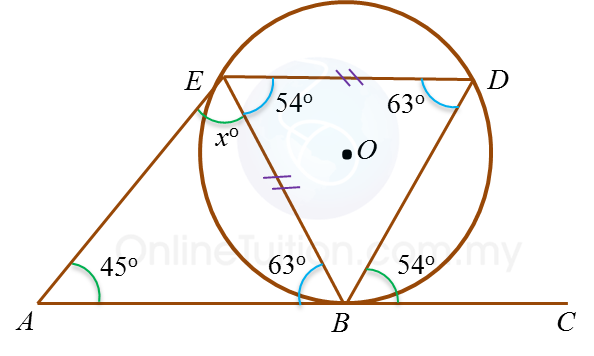
∠BED=∠CBD=54∘∠BDE=180∘−54∘2=63∘←Isosceles triangle∠EBD=∠EDB∠ABE=∠BDE=63∘In△ABE,x∘+45∘+63∘=180∘x∘+108∘=180∘x=72

8.2 Angle between Tangent and Chord (Example 1 & 2)
Example 1:
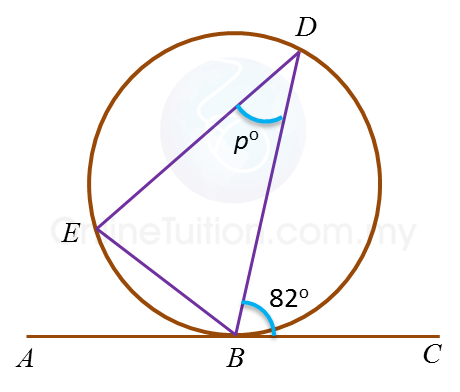

In the diagram, ABC is a tangent to the circle BDE at B.
The length of arc BD is equal to the length of arc DE.
Find the value of p.
Solution:
Angle BED = 82o ← (angle in alternate segment)
Angle DBE = 82o ← (Arc BD = Arc DE, BDE is an isosceles triangle)
Therefore p= 180o – 82o – 82o = 16o
Example 2:
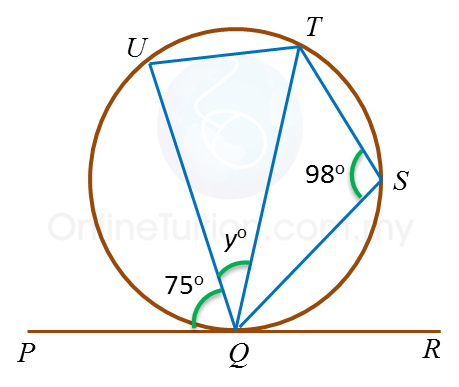
In the diagram, PQR is a tangent to the circle QSTU at Q.

Find the value of y.
Solution:
Angle QUT
= 180o– 98o ← (opposite angle in cyclic quadrilateral QSTU )
= 82o
Angle QTU = 75o ← (angle in alternate segment)
Therefore y= 180o – (82o + 75o) ← (Sum of interior angles in ∆ QTU)
= 23o




