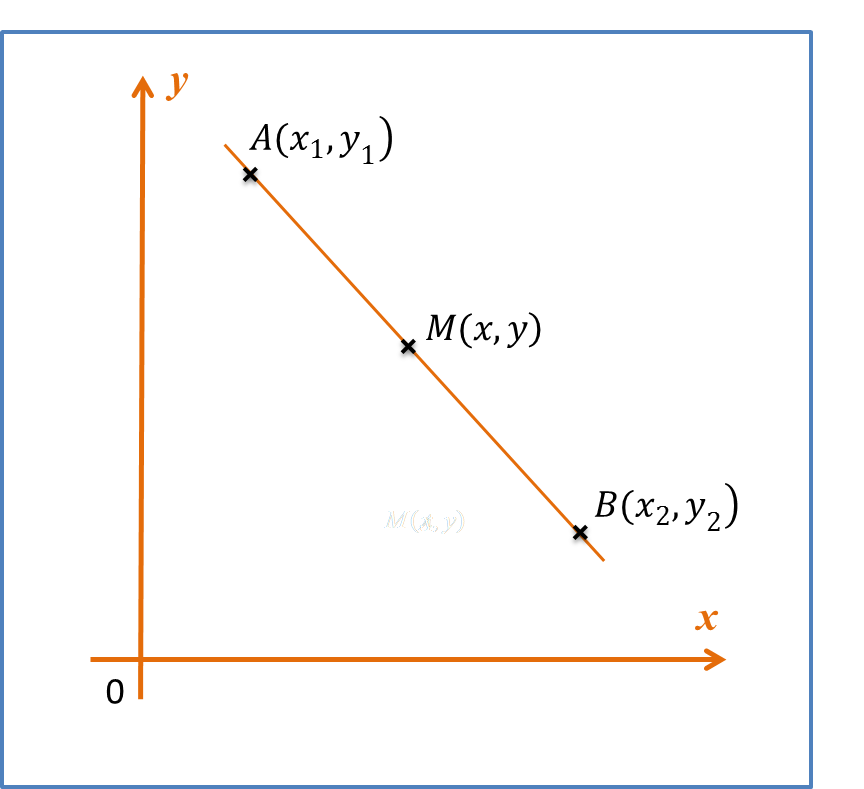
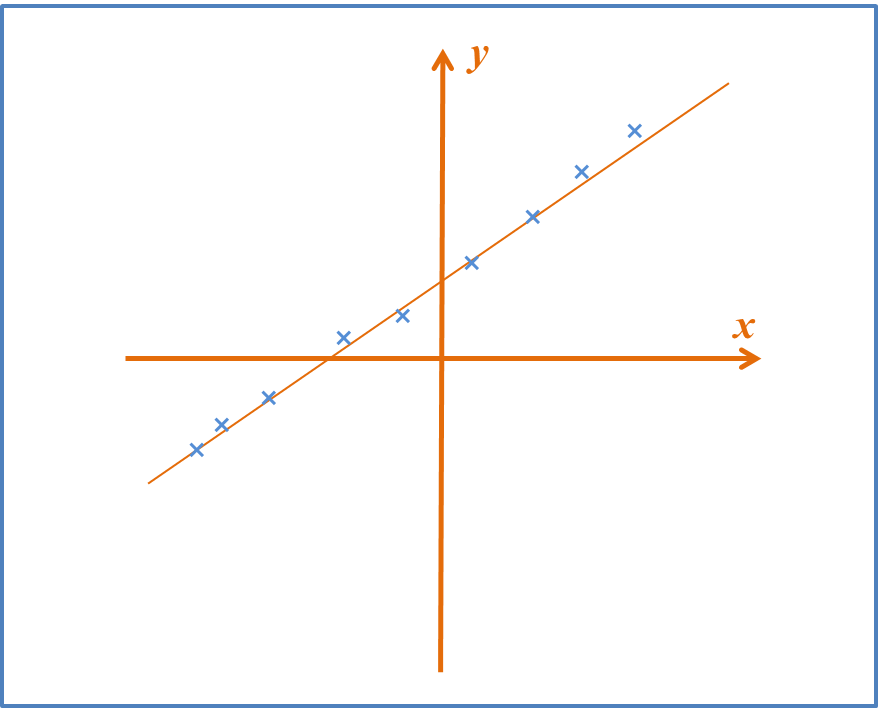
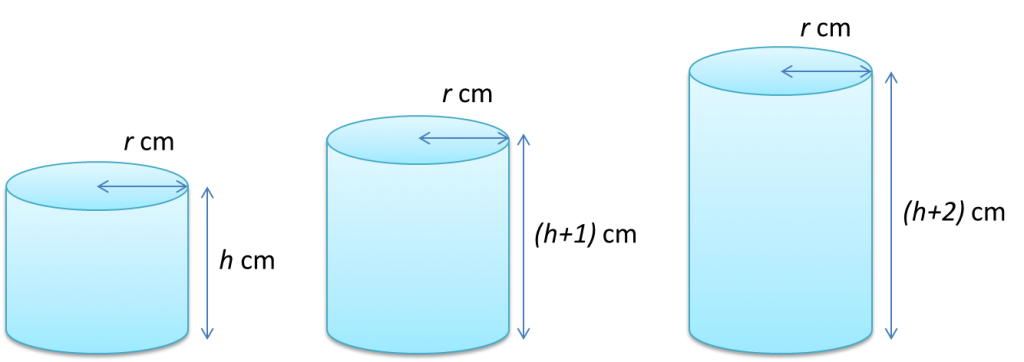
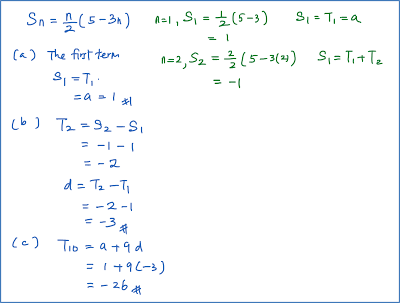Examples:
Reduce each of the following equations to the linear form. Hence, state the gradient and the Y-intercept of the linear equations in terms of  a and b.
(a)  $y=a{x}^3+b{x}^2$
(b)  $y=ax+\frac{b}{x}$
(c)  $y=ax-b{x}^2$
(d)  $xy=\frac{p}{x}+qx$
(e)  $y=a\sqrt{x}+\frac{b}{\sqrt{x}}$
(f)  $\frac{a}{y}=\frac{b}{x}+1$

[Note :
X and Y cannot have constant, but can have the variables (for example x and y)
 m and c can only have the constant(for example a and b), cannot have the variables x and y]

Solution:

(C) Mid Point 



Mid Point AB is given by $$M=\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)$$

2.2 The Line of Best Fit

Line of best fit has 2 characteristics:
(i) it passes through as many points as possible,
(ii) the number of points which are not on the line of best fit are equally distributed on the both sides of the line.

Question 2 (10 marks):
Use a graph to answer this question.
Table shows the values of two variables, x and y, obtained from an experiment. A straight line will be obtained when a graph of $\frac{y^2}{x}\text{ against }\frac{1}{x}$ is plotted.


(a) Based on Table, construct a table for the values of $\frac{1}{x}\text{ and }\frac{y^2}{x}.$  
$\begin{array}{l}\left(b\right)\text{ Plot }\frac{y^2}{x}\text{ against }\frac{1}{x}\text{, using a scale of 2 cm to 0}\text{.1 unit on the }\frac{1}{x}\text{-axis}\\ \text{ and 2cm to 2 units on the }\frac{y^2}{x}\text{-axis}\text{.}\\ \text{ Hence, draw the line of best fit}\text{.}\end{array}$

(c) Using the graph in 11(b)
(i) find the value of y when x = 2.7,
(ii) express y in terms of x.

Solution:
(a)


(b)


(c)(i)
$\begin{array}{l}\text{When }x=2.7,\frac{1}{x}=0.37\\ \text{From graph,}\\ \frac{y^2}{x}=5.2\\ \frac{y^2}{2.7}=5.2\\ y=3.75\end{array}$


(c)(ii)
$\begin{array}{l}\text{Form graph, }y\text{-intercept, }c\text{ = –4}\\ \text{gradient, }m=\frac{16-\left(-4\right)}{0.8-0}=25\\ Y=mX+c\\ \frac{y^2}{x}=25\left(\frac{1}{x}\right)-4\\ y=\sqrt{25-4x}\end{array}$