Home › View all posts by user › Page 36

Author: user

5.1 Indices and Laws of Indices (Part 2)

Posted on by

5.1 Indices and Laws of Indices (Part 2)

(C) Fractional Indices
   a 1 n  is a  n th root of  a .    a 1 n = a n    a m n  is a  n th root of  a m .    a m n = a m n

Example 1:
Find the value of the followings:
(a) 81 1 2 (b) 64 1 3 (c) 625 1 4

Solution:
(a) 81 1 2 = 81 = 9 (b) 64 1 3 = 64 3 = 4 (c) 625 1 4 = 625 4 = 5

Example 2:
Find the value of the followings:
(a)  16 3 2 (b)  ( 27 64 ) 2 3

Solution:
(a)  16 3 2 = ( 16 1 2 ) 3 = 4 3 = 64 (b)  ( 27 64 ) 2 3 = ( 27 64 3 ) 2 = ( 3 4 ) 2 = 9 16



(D) Laws of Indices

   a m × a n = a m + n   Example:    3 3 × 3 2    = 3 3 + 2 = 3 5 = 243   


   a m ÷ a n = a m − n    or    a m a n = a m − n , a ≠ 0      Example:    3 3 ÷ 3 2    = 3 3 − 2 = 3 1 = 3   or    3 3 3 2 = 3 3 − 2 = 3 1 = 3


   ( a m ) n = a m n   Example:    ( 7 3 ) 4 = 7 3 × 4 = 7 12   


   ( a b ) n = a n b n   Example:    ( 15 ) 3 = ( 5 × 3 ) 3 = 2 3 × 3 3     


   ( a b ) n = a n b n ,   b ≠ 0   Example:    ( 3 5 ) 4 = 3 4 5 4 = 81 625   

Indices and Laws of Indices (Part 1)

Posted on by

Positive Integral Indices
When a real number a is multiplied by itself n times, the result is the nth power of a.

Example:  5×5×5×5 = 54 (5 to the power of 4)

In general, if a is any real number and n is a positive integer, then


The integer n is called the index or exponent and a is the base.



5.1 Indices and Laws of Indices (Part 1)
(A) Zero Indices
The zero index of any number is equal to one.

  a 0 = 1, where a ≠ 0

Example 1:
Find the value of the followings:
(a) 2500
(b) 0.5130
(c)  ( 2 7 ) 0 (d)  ( − 11 1 25 ) 0

Solution:
(a) 2500 = 1
(b) 0.5130 = 1
(c)  ( 2 7 ) 0 = 1 (d)  ( − 11 1 25 ) 0 = 1



(B) Negative Integral Indices

   a −n  is a reciprocal of  a n .      a −n = 1 a n

Example 2:
Find the value of the followings:
(a) 102 -1
(b)  –6 -3
(c)  ( 1 3 ) − 4 (d)  ( 2 5 ) − 2 (e)  − ( 2 5 ) − 4

Solution:
(a)  102 − 1 = 1 102 (b)  − 6 − 3 = 1 − 6 3 = − 1 216 (c)  ( 1 3 ) − 4 = ( 3 ) 4 = 81 (d)  ( 2 5 ) − 2 = ( 5 2 ) 2 = 25 4 (e)  ( − 2 5 ) − 4 = ( − 5 2 ) 4 = 625 16

Quadratic Functions, SPM Practice (Long Questions)

Posted on by

Question 3:
Given that the quadratic function f(x) = 2x2 – px + p has a minimum value of –18 at x = 1.
(a) Find the values of p and q.
(b) With the value of p and q found in (a), find the values of x, where graph f(x) cuts the x-axis.
(c) Hence, sketch the graph of f(x).

Solution:
(a)
f( x )=2 x 2 −px+q =2[ x 2 − p 2 x+ q 2 ] =2[ ( x+ −p 4 ) 2 − ( −p 4 ) 2 + q 2 ] =2[ ( x− p 4 ) 2 − p 2 16 + q 2 ] =2 ( x− p 4 ) 2 − p 2 8 +q


∴ p 4 =1−−−−−−( 1 ) and − p 2 8 +q=−18−−−( 2 ) From( 1 ),p=4. Substitute p=4 into ( 2 ): − ( 4 ) 2 8 +q=−18   − 16 8 +q=−18  q=−18+2    =−16


(b)
f( x )=2 x 2 −4x−16 f( x )=0 when it cuts x-axis 2 x 2 −4x−16=0 x 2 −2x−8=0 ( x−4 )( x+2 )=0 x=4,−2 Graph f( x ) cuts x-axis at x=−2 and x=4.

(c)

Quadratic Functions, SPM Practice (Short Questions)

Posted on by

Question 3:
The straight line y = 5x – 1 does not intersect with the curve y = 2x2 + x + h.
Find the range of values of h.

Solution:
y=5x−1         ...... (1) y=2 x 2 +x+h ...... (2) Substitute (1) into (2), 5x−1=2 x 2 +x+h 2 x 2 +x+h−5x+1=0 2 x 2 −4x+h+1=0                   b 2 −4ac<0 ( −4 ) 2 −4( 2 )( h+1 )<0              16−8h−8<0                             8<8h                             h>1

Question 4:
Find the maximum value of the function 5 – x – 2x2 , and the corresponding value of x.

Solution:
5−x−2 x 2 =−2 x 2 −x+5 =−2[ x 2 + 1 2 x− 5 2 ] =−2[ x 2 + 1 2 x+ ( 1 4 ) 2 − ( 1 4 ) 2 − 5 2 ] =−2[ ( x+ 1 4 ) 2 − 1 16 − 5 2 ] =−2[ ( x+ 1 4 ) 2 − 41 16 ] =−2 ( x+ 1 4 ) 2 +5 1 8


5−x−2 x 2  has a maximum value when 2 ( x+ 1 4 ) 2 =0               x=− 1 4 The maximum value of 5−x−2 x 2  is 5 1 8 .

Quadratic Functions, SPM Practice (Short Questions)

Posted on by

Question 1:

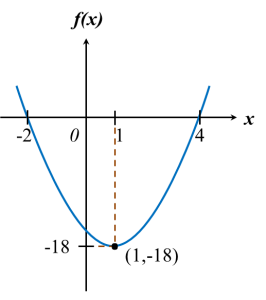
Find the minimum value of the function f (x) = 2x2 + 6x + 5. State the value of xthat makes f (x) a minimum value.

Solution:

By completing the square for f (x) in the form of f (x) = a(x + p)2 + q to find the minimum value of f (x).

f ( x ) = 2 x 2 + 6 x + 5 = 2 [ x 2 + 3 x + 5 2 ] = 2 [ x 2 + 3 x + ( 3 × 1 2 ) 2 − ( 3 × 1 2 ) 2 + 5 2 ]
= 2 [ ( x + 3 2 ) 2 − 9 4 + 5 2 ] = 2 [ ( x + 3 2 ) 2 + 1 4 ] = 2 ( x + 3 2 ) 2 + 1 2

Since a = 2 > 0,
Therefore f (x) has a minimum value when x = − 3 2 . . The minimum value of f (x) = ½. 

Question 2:

The quadratic function f (x) = –x2 + 4x + k2, where k is a constant, has a maximum value of 8.
Find the possible values of k.

Solution:
f (x) = –x2 + 4x + k2
f (x) = –(x2 – 4x) + k2 ← [completing the square for f (x) in
the form of f (x) = a(x + p)2+ q]
f (x) = –[x2 – 4x + (–2)2 – (–2)2] + k2
f (x) = –[(x – 2)2 – 4] + k2
f (x) = –(x – 2)2 + 4 + k2

Given the maximum value is 8.
Therefore, 4 + k2 = 8
k2 = 4
k = ±2

 

 

 

 

3.4 Quadratic Inequalities (Part 2)

Posted on by
(C) Linear Inequality 

Example 1
(a)  Given x = 6 − y 3  , find the range of values of x for which y > 9 .
(b) Given 2 x + 3 y − 6 = 0  , find the range of values of x for which y < 4 .






(D) Quadratic Inequalities 

Example 2
Find the range of values of x which satisfy  the following inequalities:
(a) (2x + 1) (3x – 1) < 14
(b) (x– 2) (5x – 4) + 1 > 0

3.2 Maximum and Minimum Value of Quadratic Functions

Posted on by

Maximum and Minimum Point

  1. A quadratic functions f ( x ) = a x 2 + b x + c can be expressed in the form f ( x ) = a ( x + p ) 2 + q by the method of completing the square.
  2. The minimum/maximum point can be determined from the equation in this form f ( x ) = a ( x + p ) 2 + q .
Minimum Point
  1. The quadratic function f(x) has a minimum value if a is positive. 
  2. The quadratic function f(x) has a minimum value when (x + p) = 0
  3. The minimum value is equal to q.
  4. Hence the minimum point is (-p, q)

Maximum Point

  1. The quadratic function f(x) has a maximum value if a is negative.
  2. The quadratic function f(x) has a maximum value when (x + p) = 0
  3. The maximum value is equal to q.
  4. Hence the maximum point is (-p, q)



Example
Find the maximum or minimum point of the following quadratic equations
a. f ( x ) = ( x − 3 ) 2 + 7
b. f ( x ) = − 5 − 3 ( x + 15 ) 2

Answer:
(a)
f ( x ) = ( x − 3 ) 2 + 7 a = 1 , p = − 3 , q = 7 a > 0 ,  the quadratic function has a minimum point Minimum point = ( − p , q ) = ( 3 , 7 )

(b)
f ( x ) = − 5 − 3 ( x + 15 ) 2 a = − 3 ,   p = 15 ,   q = − 5 a < 0 ,  the quadratic function has a maximum point Maximum point = ( − p , q ) = ( − 15 , − 5 )

Quadratic Equations, SPM Practice (Paper 2)

Posted on by

Question 4:
It is given α and β are the roots of the quadratic equation x (x – 3) = 2k – 4, where k is a constant.
 (a) Find the range of values of k if α≠β. (b) Given  α 2  and  β 2  are the roots of another quadratic equation      2 x 2 +tx−4=0, where t is a constant, find the value of t and of k.

Solution:
(a) x( x−3 )=2k−4 x 2 −3x+4−2k=0 a=1, b=−3, c=4−2k                     b 2 −4ac>0 ( −3 ) 2 −4( 1 )( 4−2k )>0                9−16+8k>0                             8k>7                               k> 7 8

(b) From the equation  x 2 −3x+4−2k=0, α+β=− b a          =− −3 1          =3.............( 1 ) αβ= c a     = 4−2k 1     =4−2k.............( 2 ) From the equation 2 x 2 +tx−4=0, α 2 + β 2 =− t 2 α+β=−t.............( 3 ) α 2 × β 2 =− 4 2 αβ=−8.............( 4 ) Substitute (1)=(3), 3=−t t=−3 Substitute (2)=(4), 4−2k=−8 4+8=2k k=6

Quadratic Equations, SPM Practice (Paper 2)

Posted on by

2.10.2 Quadratic Equations, SPM Practice (Paper 2)

Question 3:
If α and β are the roots of the quadratic equation 3x2 + 2x– 5 = 0, form the quadratic equations that have the following roots.
(a)  2 α  and  2 β (b)  ( α + 2 β )  and  ( β + 2 α )

Solution:
3x2 + 2x – 5 = 0
a = 3, b = 2, c = –5
The roots are α and β.
α + β = − b a = − 2 3 α β = c a = − 5 3

(a)
The new roots are  2 α and 2 β . Sum of new roots = 2 α + 2 β = 2 β + 2 α α β = 2 ( α + β ) α β = 2 ( − 2 3 ) − 5 3 = 4 5

Product of new roots = ( 2 α ) ( 2 β ) = 4 α β = 4 − 5 3 = − 12 5

Using the formula, x2– (sum of roots)x + product of roots = 0
The new quadratic equation is
x 2 − ( 4 5 ) x + ( − 12 5 ) = 0
5x2 – 4x– 12 = 0



(b)
The new roots are  ( α + 2 β ) and ( β + 2 α ) . Sum of new roots = ( α + 2 β ) + ( β + 2 α )
= α + β + ( 2 α + 2 β ) = α + β + 2 α + 2 β α β = α + β + 2 ( α + β ) α β = 4 5 + 2 ( 4 5 ) − 12 5 = 4 5 − 2 3 = 2 15
Product of new roots = ( α + 2 β ) ( β + 2 α ) = α β + 2 + 2 + 4 α β
= − 12 5 + 4 + 4 − 12 5 = − 12 5 + 4 − 5 3 = − 1 15

The new quadratic equation is
x 2 − ( 2 15 ) x + ( − 1 15 ) = 0
15x2 – 2x– 1 = 0

Quadratic Equations, SPM Practice (Paper 2)

Posted on by


Question 2:
Given α and β are two roots of the quadratic equation (2x + 5)(x + 1) + p = 0 where αβ = 3 and p is a constant.
Find the value p, α and of β.

Solutions:
(2x + 5)(x + 1) + p = 0
2x2 + 2x + 5x + 5 + p = 0
2x2 + 7x + 5 + p = 0
*Compare with, x2– (sum of roots)x + product of roots = 0
x 2 + 7 2 x + 5 + p 2 = 0 ← divide both  sides with 2
Product of roots, αβ = 3
5 + p 2 = 3  
5 + p = 6
p = 1

Sum of roots = − 7 2  
   α + β = − 7 2   →  (1) and  α β = 3    →  (2) from (2),  β = 3 α    →  (3) Substitute (3) into (1), α + 3 α = − 7 2  

2α2+ 6 = –7α ← (multiply both sides with 2α)
2α2+ 7α + 6 = 0
(2α + 3)(α + 2) = 0
2α + 3 = 0   or α + 2 = 0
α=− 3 2    α = –2

Substitute  α = − 3 2  into (3), β = 3 − 3 2 = 3 ( − 2 3 ) = − 2

Substitute α = –2 into (3),
β = − 3 2 ∴   p = 1 ,  and when  α = − 3 2 , β = − 2  and  α = − 2 , β = − 3 2 .