
- Blowing air into a liquid will cause the liquid evaporate faster.
- During evaporation, latent heat is absorbed from the liquid (as a surrounding) causing the temperature of the liquid decreases.
Applications of Cooling by Evaporation
Refrigerators
- The cooling effect in many refrigerators is produced by the evaporation of a volatile liquid called Freon.
- The liquid Freon evaporates rapidly in the pipes in the freezer compartment as more and more of its vapour is drawn away by the electric pump. As the Freon evaporates, it draws the necessary latent heat from the food inside the refrigerator.
- The pump compresses the vapour which turns liquid again on being forced through the zig-zag pipe at the back of the refrigerator. The latent heat released is given off through the cooling fins.
- In this way, thermal energy is extracted from the food inside the refrigerator and given out at the back. A refrigerator actually makes your kitchen warmer.
4.3.6 Evaporation and Boiling
Rate of Evaporation
- Evaporation is the process of converting a substance (such as water) from its liquid state to its gaseous state at temperature lower than the boiling point of the liquid.
- There are several ways of making a liquid evaporate faster:
- Increase its temperature
- Increase its surface area
- Pass air through it or across its surface
- Make the liquid into a fine spray
A spray is made up of millions of tiny liquid droplets with a very large total surface area. The highly curved surfaces make it easier for molecules to escape.
4.3.5 Specific Latent Heat of Vaporisation
Measuring the Specific Latent Heat of Vaporization of Water
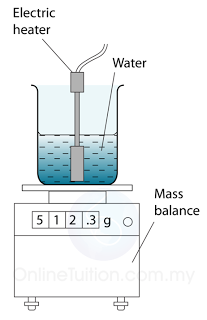
- Figure above shows the apparatus used. When the water in the can is boiling vigorously, the mass reading on the balance is noted and a stopwatch started. A few minutes later, the stopwatch is stopped and the mass reading is taken again.
- The difference in the mass readings gives the mass of water which has been changed into steam during the time measured.
Therefore, the specific latent heat of vaporisation of water can be calculated by the following equation

- The boiling point of a liquid is proportional to the air pressure of the surrounding. The higher the air pressure, the higher the boiling point.
- At higher altitude, the atmospheric pressure is lower. Therefore the boiling point of a liquid will decrease at higher altitude.
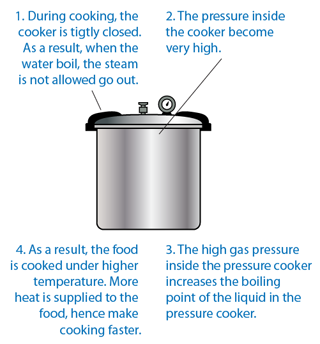
Pressure Cooker
- Pressure cooker can cook faster than normal cooker.
- The high gas pressure inside the pressure cooker increases the boiling point of the liquid in the pressure cooker.
- As a result, the food is cooked under higher temperature. More heat is supplied to the food, hence make cooking faster.
- The function of the safety valve is to release extra steam to the surrounding and consequently reduce the pressure in the pressure cooker when it is too high.
4.3.4 Specific Latent Heat
- The specific latent heat of a substance is the amount of heat requires to change the phase of 1 kg of substance at a constant temperature.
- Specific latent heat is measured in J/kg, if energy is measured in J and mass in kg.For example, specific latent heat of ice is 334000J/kg means 334000 J of energy is needed to convert 1kg of water into ice or vice versa.
Formula: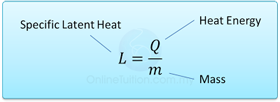
- The specific latent heat of vaporization is the heat needed to change 1 kg of a liquid at its boiling point into vapour without a change in temperature.
- The specific latent heat of fusion is the heat needed to change 1 kg of a solid at its melting point into a liquid, without a change in temperature.
- If any solid is to become a liquid, it must gain the necessary latent heat. Equally, if a liquid is to change back into a solid, it must lose this latent heat.
Measuring the Specific Latent Heat of Fusing of Ice
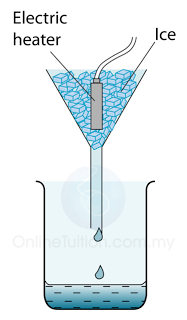
- Figure above shows the apparatus setup to determine the specific latent heat of fusion of ice. Some ice at 0 °C is heated by a small electric heater which is left switched on for several minutes.
- Some of the ice melts to form water which runs down through the funnel and is collected in the beaker.
- The mass of ice (m) melted is found by measuring the mass of water collected.
- If the power of the heater is P and the time taken to heat the ice = t, then the thermal energy supplied by the heater = thermal energy used to melt ice = Pt.
Therefore, the specific latent heat of fusion of ice
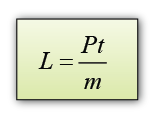
Precaution Steps:
- The heating element of the heater must fully immerse in ice so that all the heat generated is absorbed by the ice.
- A control set is needed to estimate the amount of mass of ice melted by the heat from the surrounding.
Note:
- The heat received by ice is less than the calculated value Pt as some heat is lost to the surrounding. This will result in the value of l obtained from the calculation to be slightly higher than the standard value.
- If impurity is present in water, the melting point of the water will be lower than normal.
How much heat energy is required to change 2 kg of ice at 0°C into water at 20°C? [Specific latent heat of fusion of water = 334 000 J/kg; specific heat capacity of water = 4200 J/(kg K).]
Answer:
m = 2kg
Specific latent heat of fusion of water, L = 334 000 J/kg
specific heat capacity of water = 4200 J/(kg K)
Energy needed to melt 2kg of ice,
Q1 = mL = (2)(334000) = 668000J
Energy needed to change the temperature from 0°C to °C.
Q2 = mcθ = (2)(4200)(20 - 0) = 168000J
Total energy needed = Q1 + Q2 = 668000 + 168000 = 836000J
Starting at 20°C, how much heat is required to heat 0.3 kg of aluminum to its melting point and then to convert it all to liquid? [Specific heat capacity of aluminium = 900J kg-1 °C-1; Specific latent heat of aluminium = 321,000 Jkg-1, Melting point of aluminium = 660°C]
Answer:
m = 0.3kg
Specific latent heat of fusion of aluminium, L = 321 000 J/kg
specific heat capacity of aluminium = 900 J/(kg K)
Energy needed to increase the temperature from 20°C to 660°C
Q1 = mcθ = (0.3)(900)(660 - 20) = 172,800J
Energy needed to melt 0.3kg of aluminium,
Q2 = mL = (0.3)(321000) = 96,300J
Total energy needed = Q1 + Q2 = 172,800 + 96,300 = 269,100J
How much heat must be removed by a refrigerator from 2 kg of water at 70 °C to convert it to ice cubes at -11°C? [Specific heat capacity of water = 4200J kg-1 °C-1; Specific latent heat of fusion of ice = 334,000 Jkg-1, specific heat capacity of ice = 2100 J/(kg K)]
Answer:
m = 2kg
Specific latent heat of fusion of water, L = 334,000 J/kg
Specific heat capacity of water, cw = 4,200 J/(kg K)
Specific heat capacity of ice, ci = 2,100 J/(kg K)
Energy to be removed to reduce the temperature from 70°C to 0°C (Freezing point of water)
Q1 = mcθ = (2)(4200)(70 - 0) = 588,000J
Energy needed to freeze 2kg of water,
Q2 = mL = (2)(334,000) = 668,000J
Energy to be removed to reduce the temperature from 0°C to -11°C
Q3 = mcθ = (2)(2100)(0 - (-11)) = 46,200J
Total energy needed = Q1 + Q2 + Q3 = 588,000 + 668,000 = 46,200J = 1,302,200J
4.3.3 Cooling Curve
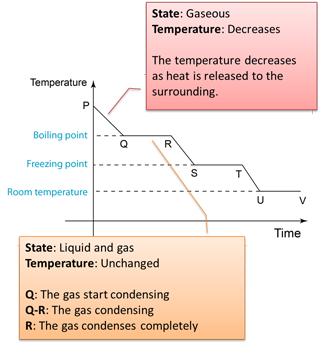
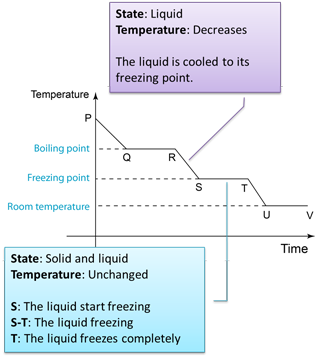
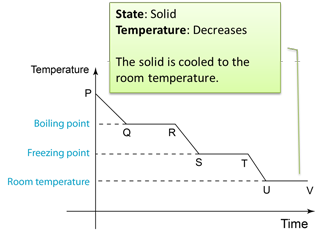
Figure below shows the change of the temperature when a gas is cooled to become solid.
Q & A
Q: Why the temperature remained unchanged from Q-R and S-T?A: The temperature remains unchanged because the heat released during the formation of the intermolecular forces compensates the heat losses to the surrounding.
Q & A
Q: Why the temperature remained unchanged from U-V?A: Because the temperature of the solid has reached the temperature of the surrounding.
4.3.2 Heating Curve
Figure below shows the change of the temperature when a solid is heated until it become gas.
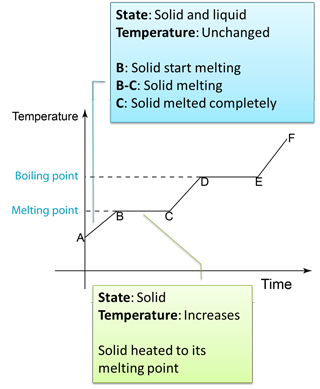
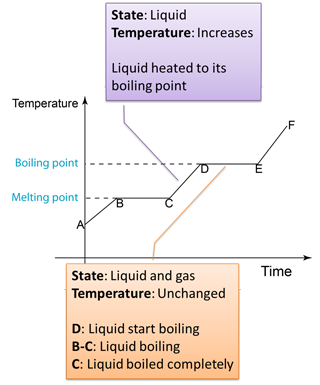
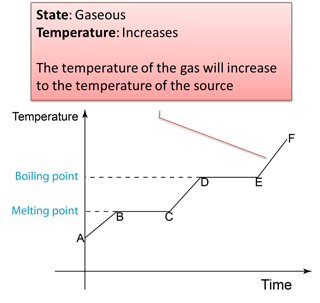
Note:
B to C
- Temperature remain unchanged because the heat absorbed is used to overcome the force between the particles in the solid.
- The heat absorbed to change a solid to liquid is called the latent heat of fusion.
D to E
- Temperature remain unchanged because the heat absorbed is used to overcome the force between the particles in the liquid and also the atmospheric pressure.
- The heat absorbed to change a liquid to gas is called the latent heat of vaporisation.
4.3.1 Latent Heat
- When a solid melt, heat is absorbed but the temperature remains constant.
- When a liquid is boiling, heat is also absorbed but the temperature again remains constant.
- The heat absorbed or given out at constant temperature during the change of phase is known as latent heat.
- The heat energy that releases during condensation or boiling is called the latent heat of vaporization.
- The heat energy that releases during freezing or melting is called the latent heat of fusion.
4.2.3 Applications of Specific Heat Capacity
Cooking Pot

- Different part of a cooking pot are made up of different material.
- The base of a cooking pot is usually made up of copper because
- copper has low specific heat capacity so that it need less heat to raise up the temperature.
- copper is a good heat conductor.
- copper has high density. The heavier base can make the pot become more stable.
- The handles of cooking pot is usually made up of plastic or wood because
- plastic and wood have high specific heat capacity. Their temperature won’t become too high even it absorbs large amount of heat.
- plastic and wood are good heat insulator.
- plastic and wood have low density hence they do not add much to the total weight of the pot.
- The body of the cooking pot is usually made up of stainless steel because
- steel has low specific heat capacity and hence need need less heat to raise up the temperature.
- steel does not react chemically with the food.
Car Engine
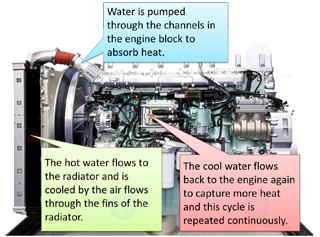
- Water is used to cool down the car engine.
- Water is used as the cooling agent in the car cooling system because
- it has high specific heat capacity. It can absorb a large amount of heat without a high increase in temperature.
- it is cheap and can be obtained easily.
- Water is pumped through the channels in the engine block to absorb heat.
- The hot water flows to the radiator and is cooled by the air flows through the fins of the radiator.
- The cool water flows back to the engine again to capture more heat and this cycle is repeated continuously.
Applications of Specific Heat Capacity - Factories with Low Ceiling
- Some factories without large machinery are constructed with low ceilings to reduce the volume of air inside the building.
- The smaller mass of air will have a smaller heat capacity.
- As a result, less heat needs to be removed to reduce the temperature of the air.
- This will then reduce the air conditioning costs for the factory.
Thermal Radiator
- Thermal radiators are always used in cold country to warm the house.
- Hot water is made to flow through a radiator. The heat given out from the radiator is then warm the air of the house.
- The cold water is then flows back to the water tank. This process is repeated continuously.
- Water is used in the radiator because it has high specific heat capacity.

Sea Breeze
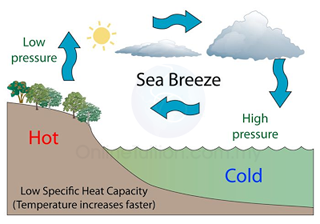
- Land has lower heat capacity than sea water. Therefore, in day time, the temperature of the land increases faster than the sea.
- Hot air (lower density) above the land rises. Cooler air from the sea flows towards land and hence produces sea breeze.
Land Breeze
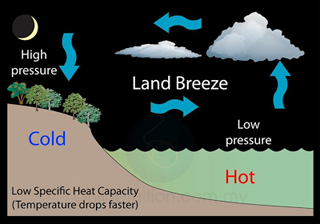
- Land has lower heat capacity than sea water. During night time, the temperature of the land drops faster than the sea.
- Hot air (lower density) above the sea rises. Cooler air from the land blows towards sea and hence produces land breeze.
Moderate Climate

- Places with the presence of lakes, sea and ocean may have more moderate climate.
- This is because, water has large specific heat capacity.
- During daytime when it is hot, the water from the lake/sea absorbs heat from the surroundings. This helps to reduce the temperature of the surroundings.
- During night-time, the water releases the heat absorbed during daytime, and hence prevents the temperature from dropping too much.
- As such, palcess near a large mass of water will have a smaller range of temperatures and hence a more moderate climate condition.
4.2.2 Specific Heat Capacity
- Specific heat capacity is a physical quantity used to compare the heat capacity of a given material of the same mass.
- It is the measure of how much energy can be store in 1 kg of mass of a substance.
- Specific heat capacity is defined as the amount of heat required to change the temperature of 1 kg of a substance by 1°C.
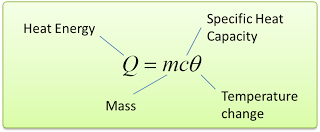
Mathematically, we write this as c = Q/mθ [Q = heat, c = specific heat capacity, m = mass, θ = change of temperature] - The SI unit of specific heat capacity is J/kg/°C.
- For example, the specific heat capacity of water is 4200 J/kg/°C means 4200J of heat energy is needed to change the temperature of 1kg water by 1°C.
- The amount of heat transferred in an object when temperature change can be calculated by using the following equation.
How much heat energy is required to change 2 kg of ice at 0°C into water at 20°C? [Specific latent heat of fusion of water = 334 000 J/kg; specific heat capacity of water = 4200 J/(kg K).]
Answer:
m = 2kg
Specific latent heat of fusion of water, L = 334 000 J/kg
specific heat capacity of water = 4200 J/(kg K)
Energy needed to melt 2kg of ice,
Q1 = mL = (2)(334000) = 668000J
Energy needed to change the temperature from 0°C to °C.
Q2 = mcθ = (2)(4200)(20 - 0) = 168000J
Total energy needed = Q1 + Q2 = 668000 + 168000 = 836000J
Starting at 20°C, how much heat is required to heat 0.3 kg of aluminum to its melting point and then to convert it all to liquid? [Specific heat capacity of aluminium = 900J kg-1 °C-1; Specific latent heat of aluminium = 321,000 Jkg-1, Melting point of aluminium = 660°C]
Answer:
m = 0.3kg
Specific latent heat of fusion of aluminium, L = 321 000 J/kg
specific heat capacity of aluminium = 900 J/(kg K)
Energy needed to increase the temperature from 20°C to 660°C
Q1 = mcθ = (0.3)(900)(660 - 20) = 172,800J
Energy needed to melt 0.3kg of aluminium,
Q2 = mL = (0.3)(321000) = 96,300J
Total energy needed = Q1 + Q2 = 172,800 + 96,300 = 269,100J
How much heat must be removed by a refrigerator from 2 kg of water at 70 °C to convert it to ice cubes at -11°C? [Specific heat capacity of water = 4200J kg-1 °C-1; Specific latent heat of fusion of ice = 334,000 Jkg-1, specific heat capacity of ice = 2100 J/(kg K)]
Answer:
m = 2kg
Specific latent heat of fusion of water, L = 334,000 J/kg
Specific heat capacity of water, cw = 4,200 J/(kg K)
Specific heat capacity of ice, ci = 2,100 J/(kg K)
Energy to be removed to reduce the temperature from 70°C to 0°C (Freezing point of water)
Q1 = mcθ = (2)(4200)(70 - 0) = 588,000J
Energy needed to freeze 2kg of water,
Q2 = mL = (2)(334,000) = 668,000J
Energy to be removed to reduce the temperature from 0°C to -11°C
Q3 = mcθ = (2)(2100)(0 - (-11)) = 46,200J
Total energy needed = Q1 + Q2 + Q3 = 588,000 + 668,000 = 46,200J = 1,302,200J
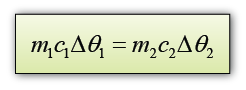
A 0.5 kg block of aluminium at a temperature of 100 °C is placed in 1.0 kg of water at 20 °C. Assuming that no thermal energy is lost to the surroundings, what will be the final temperature of the aluminium and water when they come to the same temperature? [The specific heat capacity of water is 4200 Jkg-1K-1 and The specific heat capacity of aluminium is 900 Jkg-1K-1]
Answer:
Let's say the final temperature for both aluminium block and water = θ
For aluminium,
m1 = 0.5 kg
c1 = 900 Jkg-1K-1
∆θ1 = 100 °C - θ
For water,
m2 = 1.0kg
c2 = 4200 Jkg-1K-1
∆θ2 = θ - 20 °C
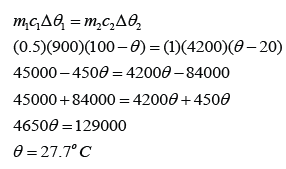
Example 2:
What will be the final temperature if 50 g of water at 0 °C is added to 250 g of water at 90 °C?
Answer:
For water at 90 °C,
m1 = 250g
c1 = c2 = c
∆θ1 = 90 °C - θ
For water at 0 °C,
m2 = 50g
∆θ2 = θ - 0 °C = θ
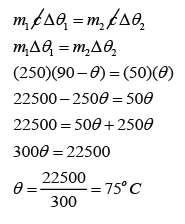
Example 3:
How much water at 10 °C is needed to cool 500 g of water at 90 °C down to 30 °C?
Answer:
For water at 90 °C,
m1 = 500g
c1 = c2 = c
∆θ1 = 90 - 30 = 60 °C
For water at 10 °C,
m2 = ?
∆θ2 = 30 - 10 = 20 °C
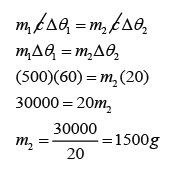
Conversion of Gravitational Energy to Thermal Energy
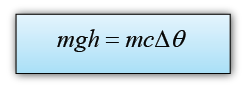
Example 1:
The Angel Falls in Venezuela is 979 m in height. Calculate the rise in temperature of the water when the water fall from the top to the bottom. (Assume that all the potential energy loss of the water is converted to heat) [The specific heat capacity of water is 4200Jkg-1K-1]
Answer:
The potential energy loss = mgh
The thermal energy gain of the water = mcθ
We assume that all the potential energy loss of the water is converted to heat, hence
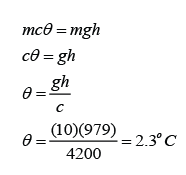
Example 2:
A mass m of lead shot is placed at the bottom of a vertical cardboard cylinder. The cylinder is 1.0 m long and closed at both ends. The cylinder is suddenly inverted so that the shot falls 1.0 m. By how much will the temperature of the shot increase if this process is repeated 200 times? Assume no heat loss to the surrounding. [The specific heat capacity of lead is 130Jkg-1K-1]
Answer:
Distance fall, h = 200 x 1m = 200m
Gratational field strength, g = 10 m/s²
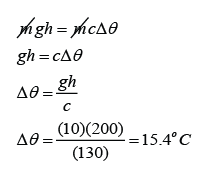
Conversion of Kinetic Energy to Thermal Energy
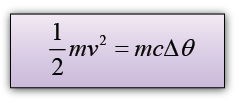
A 2.5g lead bullet is moving at 200 m/s when it strikes a wooden block and is brought to rest. If all the kinetic energy is transferred to thermal energy in the bullet, find the rise in temperature of the bullet. [The specific heat capacity of lead is 130Jkg-1K-1]
Answer:
v = 200m/s
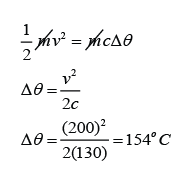
Conversion of Electrical Energy to Thermal Energy
Electrical energy, E = PtIf we assume that all the electrical energy convert into thermal energy, then
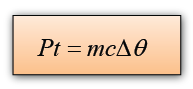
An electric heater supplies 2.5 kW of power in the form of heat to a tank of 0.02m³ of water. How long will it take to heat the water from 25 °C to 70 °C? Assume heat losses to the surroundings to be negligible. [Density of water = 1000kg/m³; The specific heat capacity of water is 4200Jkg-1K-1]
Answer:
P = 2500W
m = (0.02)(1000)=20kg
c = 4200Jkg-1K-1
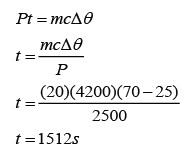
4.2.1 Heat Capacity
- Heat capacity is the measure of the ability of an object to store heat as its temperature changes.
- It is the measure of the amount of heat required to change the temperature of an object by 1°C.
- The SI unit of heat capacity is joules per Kelvin (J/K).
- The heat capacity of an object depends on the type of the material the object is made and also the mass of the object. An object with larger mass has higher heat capacity.
- An object with higher heat capacity need more heat supplied to change 1 unit of the temperature.