The examples of application of low pressure are
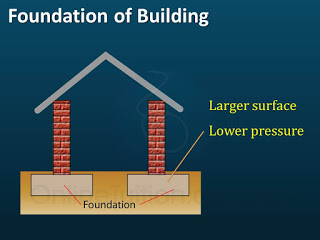
Foundation of Building
Snow Shoes
Ski Board
Tyre of Tractor
Feet of Elephant
Strip of Handbag
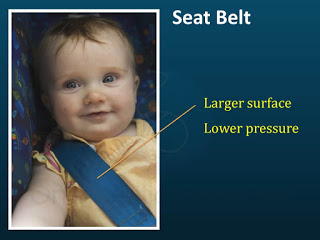
Seat Belt
3.1.3 Applications of Low Pressure
Author: user
3.1.2 Applications of High Pressure
The examples of application of high pressure are:
Sharp Knife
Ice-Skate
Sole of Shoes with Spike
3.1.1 Understanding Pressure
- The definition of pressure
- The formula of pressure (you need this formula to do lot of calculation.)
- The SI unit of pressure
- Factors affecting the magnitude of pressure
Pressure
Pressure is defined as the force acting normally per unit area. (Here, the word "normally" means perpendicularly.)
Example
As shown in the diagram above, a 20N force acts on a 4cm² surface. The force is shared equally by the surface, hence each 1 cm² of the surface withstand a force of 5N (20N/4).
The force (5N) acts on 1 unit area (1cm²) is said to be the pressure acting on the surface. Therefore, the pressure acting on the surface is 5N/cm².
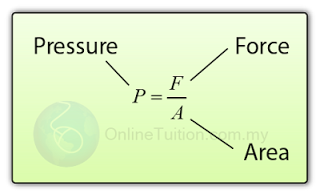
Mathematically,
Unit of Pressure
The SI unit of pressure is Pascal (Pa). 1 Pa is equal to1 newton per metre2 (N/m²).
1 N/m² = 1 Pa
Factors Affecting the Magnitude of Pressure
Factors that affect the pressure acting on a surface.- Magnitude of the force.
The larger the force, the higher the pressure. - Contact area.
The larger the contact area, the lower the pressure.
Finding the force acted on a surface when the pressure and surface area are given.
Example:
A force F is acting on a surface of area 20cm², produces a pressure 2500Pa on the surface. Find the magnitude of the force.
Answer:
This is a pretty direct question. We just need to write the formula and then substitute all the related value that we have into the formula and then solve it.
However, we need to be careful about the unit. If the pressure is in Pa, then the unit of area must be in m².
A force F is acting on a surface of area 20cm², produces a pressure 2500Pa on the surface. Find the magnitude of the force.
Answer:
This is a pretty direct question. We just need to write the formula and then substitute all the related value that we have into the formula and then solve it.
However, we need to be careful about the unit. If the pressure is in Pa, then the unit of area must be in m².
1 m² = 10000 cm²
From the question,
A = 20 cm² = 0.002 m²
P = 2500 Pa
Example 2:
b.the highest pressure
A block of wood 3 m long, 5 m wide and 1 m thick is placed on a table. If the density of the wood is 900 kgm-3, find
a. the lowest pressureb.the highest pressure
on the table due to the block.
Answer:
a.
Step 1: Finding the weight of the block
The volume of the block = 3 x 5 x 1 = 15m³.
Mass = Density x Volume
Mass of the block, m = (900)(15)= 13500 kg
Weight of the block = mg = 13500 x 10 = 135,000N
Step 2: Determine the surface area
The pressure exerted on a surface is inversely proportional to the area of the surface. The bigger the surface, the lower the pressure.
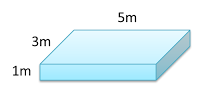
For the wooden block, the biggest surface, A = 5 x 3 = 15m²
Step 3: Finding pressure
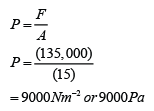
b.
The pressure is the highest when the surface area is the smallest.
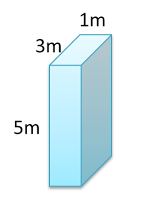
The smallest surface area of the block = 1 x 3 = 3m²
The highest pressure,
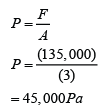
Example 3:
Two cubes made of the same material; one has sides twice as the other, lying on a table. Standing on one face, the small cube exerts a pressure M on the table. What is the pressure (in term of M) exerted by the larger cube standing on one of its faces, on the table?
Answer:
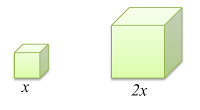
For the small cube,
Surface area = x²
Volume = x³
Mass = m
Weight = mg
Pressure,
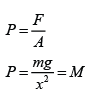
For the big cube,
Surface area = 4x²
Volume = 8x³
Mass = 8m (Because the volume is 8 times greater)
Weight = 8mg
Pressure,
2.12.5 Factors that Affect the Elasticity Springs
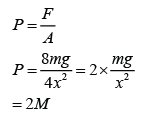
| Arrangement in series: | Arrangement in parallel: |
| Extension = x × number of spring Stiffness decreases Spring constant = k/number of spring | Extension = x ÷ number of spring Stiffness increases Spring constant = k × number of spring |
Factors Affecting the Stiffness of Spring
Material type of spring
(A steel spring is stiffer than a copper spring) |
 |
| Stiffer | Less Stiff |
Diameter of wire of spring
(The greater the diameter of the wire, the stiffer the spring) |
 |
| Stiffer | Less Stiff |
Diameter of the spring
(The smaller the diameter of spring, the stiffer the spring) |
 |
| Stiffer | Less Stiff |
Length of the string
(Shorter spring is stiffer) |
 |
| Stiffer | Less Stiff |
2.12.4 Elastic Potential Energy
Elastic Potential Energy
Elastic potential energy is the energy stored in elastic materials as the result of their stretching or compressing.Formula:
Example:
Diagram above shows a spring with a load of mass 0.5kg. The extention of the spring is 6cm, find the energy stored in the spring.
Answer:
The energy stored in the spring is the elestic potential energy.
2.12.2 Hooke’s Law
Hooke's Law states that if a spring is not stretched beyond its elastic limit, the force that acts on it is directly proportional to the extension of the spring.
Elastic Limit
The elastic limit of a spring is defined as the maximum force that can be applied to a spring such that the spring will be able to be restored to its original length when the force is removed.Equation derived from Hooke's Law
From Hook's Law, we can derived that
Spring Constant
It is a measure of the stiffness of a spring or elastic object.
Graph of Streching Force - Extension
Area below the graph = Work done
F-x graph and spring constant
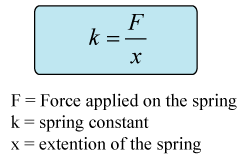
The higher the gradient, the greater the spring constant and the harder (stiffer) spring.
For example, the stiffness of spring A is greater than spring B.
2.12.1 Elasticity
Elasticity is the ability of a sub-stance to recover its original shape and size after distortion.
Forces Between Atoms
The intermolecular forces consist of an attractive force and a repulsive force.
- At the equilibrium distance d, the attractive force equal to the repulsive force.
- If the 2 atoms are brought closer, the repulsive force will dominate, produces a net repulsive force between the atoms.
- If the 2 atoms are brought furhter, the attractive force will dominate, produces a net attractive force between the atoms.
Graph of Forces Between 2 atoms
x0 = Equilibrium Distance
When the particles are compressed, x < x0, the attractive force between the particles increases.
If the distance x exceeds the elastic limit, the attractive force will decreases.
2.11.7 Efficiency
The efficiency of a device is defined as the percentage of the energy input that is transformed into useful energy.
Example:
In the example above, the input power is 100J/s, the desire output power (useful energy) is only 75J/s, the remaining power is lost as undisire output. Therefore, the efficiency of this machine is
In the example above, the input power is 100J/s, the desire output power (useful energy) is only 75J/s, the remaining power is lost as undisire output. Therefore, the efficiency of this machine is
Air Conditioner
- Switch off the air conditioner when not in use.
- Buy the air conditioner with suitable capacity according to the room size.
- Close all the doors and windows of the room to avoid the cool air in the room from flowing out.
Refrigerator
- Always remember to close the door of refrigerator.
- Open the refrigerator only when necessarily.
- Always keep the cooling coil clean.
- Defrost the refrigerator regularly.
- Choose the refrigerator with capacity suitable for the family size.
- Refrigerator of large capacity is more efficient compare with refirgerator of small capacity.
Lamp or Light Bulb
- Use fluorecent bulb rather than incandescent bulb. Fluorescent bulbs are much more efficient than incandescent bulbs.
- Use a lamp with reflector so that more light is directed towards thr desirable place.
Washing Machine
- Use front-loading washing machine rather than top-loading wahing machine because it uses less water and electricity.
- Use washing machine only when you have sufficient clothes to be washed. Try to avoid washing small amount of clothes.
2.11.6 Power
Power is the rate at which work is done, which means how fast a work is done.
It is also a measure of how fast a form energy is converted to another form.
Formula:
Example:
An electric motor takes 20 s to lift a box of mass 20kg to a height of 1.5 m. Find the amount of work done by the machine and hence find the power of the electric motor.
Answer:
Work done,
W = mgh = (20)(10)(1.5) = 300J
Power,
An electric motor takes 20 s to lift a box of mass 20kg to a height of 1.5 m. Find the amount of work done by the machine and hence find the power of the electric motor.
Answer:
Work done,
W = mgh = (20)(10)(1.5) = 300J
Power,
2.11.5 Conservation of Energy
During a conversing of energy,
Amount of Work Done = Amount of Energy Converted
Example:
A trolley of 5 kg mass moving against friction of 5 N. Its velocity at A is 4ms-1 and it stops at B after 4 seconds. What is the work done to overcome the friction?
Answer:
In this case, kinetic energy is converted into heat energy due to the friction. The work done to overcome the friction is equal to the amount of kinetic energy converted into heat energy, hence
A trolley of 5 kg mass moving against friction of 5 N. Its velocity at A is 4ms-1 and it stops at B after 4 seconds. What is the work done to overcome the friction?
Answer:
In this case, kinetic energy is converted into heat energy due to the friction. The work done to overcome the friction is equal to the amount of kinetic energy converted into heat energy, hence